ПРОБЛЕМЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ КРУПНОМАСШТАБНОЙ МАНТИЙНОЙ КОНВЕКЦИИ В ЗОНЕ СУБДУКЦИИ

1. ВВЕДЕНИЕ

В геодинамике принимается определение субдукции как «процесса погружения океанической литосферной плиты/слэба в мантию под континент или островную дугу» [Stern, 2002, с. 5], где основными движущими механизмами динамики Земли выступают заключенный в ней запас тепловой энергии [Khain, 2010] и различие плотностей между холодной субдуцирующей плитой и окружающей мантией. Достоверность этого утверждения вызвана тем, что вещество мантии ведет себя как твердое тело только при быстро меняющихся нагрузках, а при длительных нагрузках оно способно течь как вязкая жидкость [Monin, 1977]. Согласно положениям тектоники литосферных плит слэбом именуется выделяемый по данным сейсмотомографии фрагмент океанической литосферной плиты мощностью 80–100 км, погружающийся (субдуцируемый) в мантию при субдукции [Koulakov et al., 2011; Sizova et al., 2014].

Важность изучения взаимодействия мантийной конвекции и субдукции определяется значимостью проблемы характера распределения вещества геосфер, понимания строения и свойств периферических оболочек Земли. Зоны субдукции являются одними из наиболее тектонически активных участков на Земле и связаны с переносом значительных объемов вещества и энергии [Stern, 2002; Frost, 2006]. Особый интерес вызывает изучение процессов в реологически контрастных средах: конвективного в сравнительно маловязкой астеносфере и кондуктивного в твердой литосфере.

Несмотря на широту охвата проблем численного моделирования верхнемантийной конвекции [Cristensen, 1984; Schubert, Anderson, 1985; Zhong, Gurnis, 1992; Dobretsov, Kirdyashkin, 1997; Lithgow-Bertelloni, Richards, 1998; Rychkova, Tychkov, 1997; van Keken et al., 2011; Gerya, Yuen, 2003], открытыми остаются вопросы перестройки структуры мантийной конвекции при погружении слэба, дискретности характера погружения и его фрагментация, аккумуляции вещества слэба на границе верхней и нижней мантии, адаптации современных вычислительных методов для представления верхнемантийной конвекции в зоне субдукции. Принимается, что литосфера повсеместно подстилается астеносферой, вязкость которой на один-два порядка меньше таковой у литосферы [Dobretsov et al., 2001]. При этом именно здесь создаются условия для плавления вещества литосферы и формируются очаги глубинных землетрясений [Trubitsyn et al., 1993].

Цель этой работы состоит в анализе современных методов решения ряда из перечисленных вопросов, построении 2D модели динамики субдукции, в которой учитываются связанные с погружением слэба фазовые переходы его вещества, что приводит к значительному росту плотности слэба. Рассматриваются схемы решения нелинейных модельных уравнений, обсуждаются проблемы программной реализации аппарата численного моделирования.

2. МОДЕЛИ МАНТИЙНОЙ КОНВЕКЦИИ И СУБДУКЦИИ

В практике изучения субдукции принимается следующий характер взаимодействия мантийной конвекции и слэба. В частности, в работах [Zanemonets et al., 1974; Myasnikov, Markaryan, 1977; Bercovici et al., 1993] модельным приближением литосферы выступает высоковязкий кондуктивный слой квазижидкости с нулевой скоростью движения его вещества. Приближением остальной части выступает несжимаемая жидкость, реологические свойства которой характеризуются формой записи вязкости и принятыми начальными и граничными условиями. Для мантийных течений обычно принимается постоянство проскальзывания на границах расчетной области. Между тем на границах могут создаваться условия для активизации цикличности функционирования присутствующих на границе астеносфера – литосфера магматических очагов.

Для мантийной конвекции принимается положение, что она имеет химико-плотностную природу [Keondzhyan, 1980; Monin, Sorokhtin, 1981]. Тогда вследствие высокой вязкости для ее моделирования обычно используются уравнения Стокса в приближении Буссинеска [Slezkin, 1955; Landau, Lifshits, 2001]. Принятие этого приближения приводит к возможности введения фактора температуры в уравнения для завихренности и, соответственно, для скоростей.

Решение задач выполняется для разных форм представлений вязкости. Так, в терминах завихренность – функция тока в работе [McKenzie et al., 1974] изучалась тепловая конвекцию в среде с постоянной вязкостью, а в [Gurnis, Davies, 1986] – в среде, где вязкость экспоненциально возрастает с глубиной.

Модель динамики слэба, где он представлен тонкой упругой пластиной отрицательной плавучести, рассмотрена в работе [Turcotte, Schubert, 1985]. Принимается, что изгиб пластины связан с вертикальными внешними нагрузками и соотношениями для ее изгибных моментов. Численную модель субдукции составляет безразмерное уравнение для изгиба пластины под действием приложенных моментов и вертикальных нагрузок. Принимается также то, что вместе с плитой в глубины верхней мантии поступают некоторые объемы морской воды [Schubert et al., 2001]. Адаптация этого подхода для субдукции Амурской микроплиты в верхней мантии выполнена в статье [Gavrilov, Kharitonov, 2022], в которой фазовые функции следуют положениям работы [Trubitsyn V.P., Trubitsyn A.P., 2014]. Приемлемость такого подхода ограничена только первыми слоями верхней мантии, где допустимы положения Кирхгофа о сохранении нормалей к срединной поверхности деформируемой плиты и сохранении ее толщины [Timoshenko, Woinowsky-Krieger, 1966]. Однако результат сейсмического зондирования указывает на снижение толщины плиты [Fukao et al., 2009]. В частности, при ее погружении соответствующим образом растет давление и температура, что приводит к частичным потерям легких фракций вещества плиты, потерям воды и газов водосодержащих минералов, перестройкам их кристаллической решетки и последующим фазовым превращениям, а также фрагментации слэба при глубоком погружении.

Альтернативные 2D модели верхнемантийной конвекции в зоне субдукции основаны на положениях механики сплошной среды и гидродинамики, где вследствие высокой вязкости мантии уравнения движения принимаются в стоксовском приближении [Gurnis, Davies, 1986; Doglioni et al., 2006; van Keken et al., 2011; Duretz et al., 2012]. В этих моделях основной причиной субдукции выступает избыточная плотность слэба. Плотность мантии следует приближению Буссинеска. Отличия одних моделей состоят в особенностях формы записей вязкости мантии и слэба, зависимости его динамики от температуры и величин касательных напряжений [Van Keken et al., 2011], различия вариантов воздействия на плиту и вариации состава [Kincaid, Sacks, 1997].

В работе [Gerya, Yuen, 2003] представлена 2D модель термомеханической мантийной конвекции в приближении Буссинеска, где вязкость верхней мантии определяется температурой и давлением, а уравнения модели следуют токсовскому приближению. Радиоактивность, адиабатический и диссипативный нагревы мантии выступают независимыми пространственно-временными источниками тепла, исходя из чего определяется кинетика погружения слэба в толщу мантии. Вычисления основаны на включении также метода маркеров и ячеек. Решение интерполируется обратно в конфигурацию эйлеровой сетки на каждом временном шаге. При таком подходе требуются значительные вычислительные ресурсы. Достаточно отметить, что моделирование континентальной коллизии в докембрии [Zakharov et al., 2015] выполнялось на суперкомпьютерном комплексе МГУ им. М.В. Ломоносова.

В работах [Dobretsov, Kirdyashkin, 1997; Dobretsov et al., 2001, 2009; Koulakov et al., 2011] изучаются теплофизические характеристики модели только корового слоя, который выступает пограничным слоем между мантией и слэбом. Однако влияние мантийных течений на динамику слэба в этих моделях не учитывается.

В статье [Trubitsyn, 2008] рассмотрен случай, когда в уравнение для температуры участка эндотермического фазового перехода на границе верхней и нижней мантии вводится аналитическое представление функции смещения фазовой границы/распределения фаз. Показано, что эндотермический фазовый переход на глубине 660 км не приводит к расслоению конвекции. Отмечается торможение и деформация аномально холодных нисходящих потоков. Модельным образом слэба выступает область среды пониженной температуры, а его динамика определяется теми же уравнениями мантийной конвекции. Отсутствие модельного образа слэба как реального объекта системы верхняя мантия – слэб следует отнести к недостаткам такого подхода.

В работе [Bobrov, Baranov, 2014] в соотношении для вязкости учитывается пластический характер деформации, в результате чего отмечается скачкообразное перемещение зон субдукции; обнаруживаются резкие изменения в полях напряжений в зависимости от стадии отделения слэба. В областях, не содержащих погружающихся слэбов, напряжения сильно понижены. На общей картине динамики температуры участки слэба определяются сгущением изотерм. Отсутствие модельного образа слэба как реального объекта системы верхняя мантия – слэб следует отнести к недостаткам такого подхода.

В статье [Lobkovskii, Ramazanov, 2021] применение метода Галеркина и разложение в ряд Фурье лежат в основе построения аналитического представления стационарного решения уравнений модели мантийной конвекции, вещество которой определяется холодным потоком жидкости. Приводятся результаты вычислительных экспериментов вариаций структуры конвективных ячеек в зависимости от числа Рэлея. Здесь также отсутствие модельного образа слэба как реального объекта системы верхняя мантия – слэб следует отнести к недостаткам такого подхода.

В перечисленных работах не рассматриваются вопросы трансформации водосодержащих минералов слэба, которая происходит за счет выжимания воды в верхних слоях мантии. Кроме того, во многих случаях отсутствует представление слэба как самостоятельного геодинамического объекта.

3. ДИНАМИКА ФОРМИРОВАНИЯ И ПОГРУЖЕНИЯ СЛЭБА

Модель мантийной динамики в зоне субдукции здесь составляют связанные между собой системы уравнений, первая из которых определяет мантийную динамику, а вторая – погружение на фоне конвертируемой мантии более холодной и более плотной океанической плиты. Модельным представлением мантии здесь выступает двумерная несжимаемая ньютоновская жидкость в декартовой системе координат. Вследствие высокой вязкости мантии квазистационарные конвективные двумерные течения определяются известными уравнениями Стокса, безразмерная запись которых в терминах завихренность – функция тока принимает вид [Torrance, Turcotte, 1971; Turcotte, Schubert, 2002]:

(1)

(2)

(3)

(4)

где безразмерные переменные принимают такой смысл: x, y – оси декартовой системы координат (x=y=0 левый угол), ось y направлена вниз;

 – 2D оператор Лапласа;

μ(T,y), ξ(x,y,t), ψ(x,y,t), ρ(x,y,t) – динамическая вязкость мантии, завихренность, функция тока мантийных течений и ее плотность; U(x,y,t)=ψ_y, V(x,y,t)=–ψ_x, T(x,y,t) – латеральная и вертикальная скорость мантийных течений, распределение температуры в мантии;

 – плотностное число Рэлея верхней мантии;

 – ускорение свободного падения, характерные значения плотности и скорости мантийных течений, а также коэффициент теплового расширения и глубина верхней мантии; dT=T_max–T_min – характерный перепад температуры в верхней мантии; χ_ρ – коэффициент диффузии плотности горных пород; нижние индексы переменных указывают на соответствующие одноименные частные производные.

Переход от скоростей жидкости к завихренности (1) позволяет избежать явного присутствия давления.

Обезразмеривание (1)–(3) выполнялось стандартным образом (штрихом отмечены безразмерные переменные):

где переменные с верхней чертой – их характерные значения; λ и χ – теплопроводность и температуропроводность мантии, а С_Р – удельная изобарическая теплоемкость; в безразмерных уравнениях далее штрихи опускаются.

Область вычислений представляет двумерную прямоугольную область декартовой системы координат. Для граничных условий принимается отсутствие потоков тепла и вещества на боковых гранях области; потоки тепла и вещества на верхней g_T,0, g_ρ,0 и нижней g_T,H, g_ρ,H гранях области вычислений:

(5)

где x_max – безразмерная латеральная протяженность.

Для функции тока принимается условие прилипания на боковых границах ψ(0,y,t)=ψ(x_max,y,t)=0, ψ_n(0,y,t)=ψ_n(x_max,y,t)=0, где n – нормаль [Lobkovsky et al., 2013, 2021]. На участке верхней мантии, где океаническая плита движется к участку погружения, и на всей подошве мантии принимается условие проскальзывания:

при y=0 интервал X – это горизонтальный участок верхней мантии, где плита движется к месту своего погружения, а при y=1 интервал X – латеральная составляющая x; на твердых границах (в том числе и на границах со слэбом) функция тока равна нулю; значение завихренности определяется соотношением Тома [Roache, 1980]:

(6)

Анализ профилей сейсмотомографии [Stern, 2002; Fukao et al., 2009] показывает существенное превышение протяженности слэба над его толщиной, что позволяет допускать представление его модельного образа посредством гибкого тонкого стержня и независимость горизонтальной скорости погружения от вертикальной y координаты и вертикальной скорости погружения от x координаты. Принимается также гидростатичность состояния слэба и представление его плотности смесью тяжелой ρ_H=const и легкой ρ_L=const составляющих (твердым раствором). Погружение слэба происходит при условии ρ^*–ρ˃0. Тогда модель субдукции можно определить такими безразмерными уравнениями:

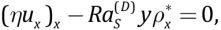(7)

(8)

(9)

(10)

(11)

 – плотностное число Рэлея для слэба;

C(x,y,t) – концентрация тяжелой составляющей слэба; B(C,ρ^*) определяет динамику частичных фазовых превращений его вещества вследствие всплытия или удаления легких составляющих вещества слэба.

При формулировке B(C,ρ^*) здесь принимаются следующие допущения. Морская вода, просачиваясь через трещины и поры в океаническую литосферу, вступает в реакцию с минералами в земной коре и мантии с образованием водных минералов (таких как серпентин), которые накапливают воду в своих кристаллических структурах [Turcotte, Schubert, 1985], поэтому при погружении слэба происходят различные трансформации таких минералов (в частности, формирование более плотных упаковок минералов за счет выжимания воды), что можно интерпретировать как частичный фазовый переход его вещества. В этой ситуации на границе мантия – слэб аккумулируются большие объемы насыщенных газами и водой таких образований (флюидов) [Dobretsov et al., 2017], что в последующем может вызвать сейсмичность и частичное плавление вещества субдуцируемой плиты [Gerya et al., 2004]. Далее, при погружении слэба повышается давление и температура среды, что обусловливает удаление/всплытие легкой составляющей и, как результат, рост концентрации тяжелой составляющей и последующее утяжеление вещества слэба. Механизм этого процесса видится в следующем. На ранних этапах погружения слэба, когда его вещество перенасыщено просочившимися сюда объемами морской воды (и, соответственно, легкими составляющими), повышение температуры и давления среды приводит к интенсивному всплытию и формированию затем избыточных объемов высокотемпературных и насыщенных газами компонент. До момента, когда плотность слэба оказывается близкой плотности среды, его погружение снижается, создаются застойные участки аккумуляции вещества слэба. Дело в том, что воздействие мантийных течений и неравномерность распределения вдоль слэба его плотности приводят к различию вдоль него напряжений, последующих деформаций и к его фрагментациям. Происходит так называемая стагнация слэба, границы которой отчетливо прослеживаются по гипоцентрам глубоких землетрясений. Их максимальная зафиксированная глубина не превышает 700 км [Stern, 2002; Fukao et al., 2009], в частности под Южной и Центральной Америкой [Stern, 2002]. Далее по мере роста концентрации тяжелой компоненты слэба происходит прорыв зоны стагнации и затем погружение этих фрагментов вплоть до ядра Земли [Agrusta et al., 2017].

Простая запись такого механизма здесь определяется соотношением:

(12)

Сейсмическая томография верхней мантии показывает нерегулярный характер границы раздела мантия – слэб, что вызвано в основном воздействием на слэб мантийных течений. При этом толщина слэба существенно меньше его протяженности, вследствие чего допускается представление его модельного образа посредством гибкого и тонкого стержня, на который эти течения воздействуют. В этой ситуации потребность нахождения частных производных для решения (7)–(10) в криволинейной области с динамической и нерегулярной границей обусловливает применение адекватных бессеточных методов. Здесь уместным видится применение бессеточного лагранжевого метода гидродинамических сглаженных частиц (SPH) [Monaghan, 2005]. Основанием метода служит представление объекта исследования (в данном случае слэба) конечным множеством дискретных элементов/частиц [Harlow, 1967], которые выступают носителями таких свойств, как плотность, положение в пространстве, скорость и набор дополнительных атрибутов.

Сущность метода состоит в том, что некоторая физическая характеристика отдельной частицы в точке определяется взвешенной суммой этой величины для других частиц:

(13)

которые лежат в окрестности

m_j, ρ_j – масса и плотность частицы c номером a,

и h (так называемая длина сглаживания);

 – аналитически заданная функция ядра, посредством которой сглаживаются свойства частиц и учитывается их взаимное влияние. Сглаживающая функция определяет вес влияния каждой частицы на вычисляемую величину. Чем ближе соседняя частица к той частице, для которой вычисляется величина атрибута, тем, соответственно, больше ее влияние на результат и тем больше сглаживающая функция в этой позиции [Aliev, 2008; Medin, Parshikov, 2010]. В этой ситуации вычисление частных производных сводится к их вычислению для аналитически заданной функции:

где b, a – порядковые номера частиц, b, a=1÷N(t); N(t) – текущее суммарное количество частиц метода; x_ba=x_b–x_a, y_ba=y_b–y_a и  – функция ядра, на основании которой аналитически рассчитываются производные в квадратных скобках. Представление лапласиана следует работе [Brookshaw, 1985]. В качестве функции ядра использовался сплайн 3‑й степени:

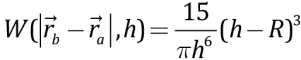при 0<R<h,

и при R>h;

[Monaghan, 2005].

Здесь при использовании метода SPH запись уравнения теплообмена для b‑й частицы принимает вид:

(14)

где c_P,b, T_b, T_a, k_b, k_a, x_a, y_a – теплоемкость, температура, коэффициент теплопроводности и координаты соответствующих частиц. Для момента t+1 они определяются соотношениями:

(15)

где  – латеральная и вертикальная скорость частиц, которые при заданных начальных и граничных условиях определяются методом SPH из уравнений (7) и (8).

4. ВЫЧИСЛИТЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ

Расчетная равномерная сетка:

строится следующим образом: x_i=x_i–1+dx, y_j=y_j–1+dy, где dx и dy – размеры шагов по осям; N_x и N_y – количество шагов по осям координат; безразмерный временной шаг dt принимается const. Принимается гидростатичность давления, а соотношение для безразмерной вязкости верхней мантии и слэба определяется выражением:

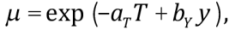
где a_T=–0.2 и b_Y=1.33 [Trubitsyn et al., 1993; Bobrov, Baranov, 2014].

Начальные распределения для температуры и плотности определяются соотношениями:

Вычислительный алгоритм состоит в следующем. Сначала в области вычислений устанавливается режим мантийной конвекции, для чего при заданных начальных и граничных условиях (5) на регулярной сетке находятся решения уравнений (1)–(4). Функция тока на границе мантия – слэб равна нулю, а значение завихренности следует (6). Решение (7)–(11) выполняется по такой схеме. Для участка поступления слэба в мантию (ячейка (x_A,1) вычислительной схемы) формируется выборка частиц с фиксированным набором характеристик (скорость, температура, плотность). Далее динамика частиц следует уравнениям (7)–(15). Воздействие мантийных течений на динамику субдукции здесь учитывается дополнением модельного образа слэба наборами неразличимых между собой частиц из примыкающих к ним в текущий момент ячеек мантии.

Модель состояния мантийной конвекции в зоне субдукции после 500 временных итераций (более 4 млн лет) представлена на рис. 1, где крупные точки характеризуют координаты участков слэба (для наглядности здесь и далее масштаб функции тока увеличен в 1000 раз).

Анализ рис. 1 показывает плавный характер течений, где функция тока в центре ячейки в семь раз превосходит ее значения на границах области. Отмечается слабая изменчивость составляющих тепломассопереноса, что связано с балансом их потоков между соседними геосферами. Согласно условиям задачи, на границе области выполняется условие прилипания и равенство нулю функции тока на границе. Поскольку граница между мантией и слэбом является непротекаемой, на ней функция тока также обращается в нуль, что приводит к плавному обтеканию профиля слэба.

Распределение температуры T, плотности ρ и функции тока ψ после 1500 временных итераций (более 48 млн лет) представлено на рис. 2. Для удобства и наглядности пространственно-временные особенности динамики температуры и плотности их распределения приведены в отклонениях от соответствующих значений для t=500.

Сопоставление распределений температуры и плотности для разных временных итераций показывает некоторое остывание и разуплотнение начальных слоев верхней мантии, что вызвано допущением о ненулевых потоках тепла и вещества на границах верхней мантии (условие (5)). Анализ рис. 2, б, показывает некоторую нелинейность распределения плотности: между слоями с отрицательным отклонением плотности для безразмерного t=500 следует слой плотности с положительным отклонением. Такая ситуация вызвана конвективным перемешиванием мантии. Заметен также временной рост функции тока, следовательно, и воздействия на слэб, что приводит к росту в его теле различных деформаций и вызывает затем его частичную фрагментацию.

Распределение температуры, плотности и линий тока после 1900 временных итераций (более 91 млн лет) представлено на рис. 3.

Распределение температуры показывает некоторое остывание начальных слоев верхней мантии, что связано с выносом тепла. Отмечается также некоторое разуплотнение начальных слоев, что связано с конвективным перемешиванием. Погружение плиты в мантию (субдукция) вызывает разбиение исходной конвективной ячейки на две составляющие. В этой ситуации слэб реально выступает вертикальной «перегородкой». Характер представленных на рис. 2, в, и рис. 3, в, изолиний показывает, что в непосредственной окрестности слэба создаются условия для уплотнения значений функции тока и формирований здесь мелкомасштабных вихрей (вихрей Карига [Gavrilov, Kharitonov, 2017]).

По мере приближения слэба к подошве нижней мантии отмечается его выполаживание, что связано с повышением температуры слэба в этой зоне и снижением здесь его вязкости. Такая ситуация вместе с залеганием более плотных нижележащих слоев вещества приводит к деформированию его передней части под воздействием конвективных потоков.

Проявление особенностей формирования мелкомасштабных вихрей, выполаживания и фрагментации слэба становится наглядным в масштабированной окрестности слэба на рис. 4.

Воздействие на слэб мантийных течений и неравномерность распределения вдоль него плотности обусловливают его частичную фрагментацию. Фрагменты слэба достигают кровли нижней мантии, где они и накапливаются (на этой границе допускается диффузия частиц).

5. ЗАКЛЮЧЕНИЕ

В работе рассмотрены основные положения для построения моделей субдукции в верхней мантии. Рассматривается комплексная модель, составляющими которой выступает модель мантийной конвекции (уравнения завихренности, функции тока и тепломассопереноса) и пространственно-временная модель динамики слэба (уравнения скоростей, уравнения тепломассопереноса, для решения поставленной задачи представлена адаптация метода SPH). Предлагается модель количественного учета фазовых переходов вещества слэба.

Воздействие мантийных течений на динамику субдукции здесь учитывается дополнением модельного образа слэба наборами неразличимых между собой частиц из примыкающих к ним в текущий момент ячеек мантии.

Воздействие на слэб мантийных течений и неравномерность распределения вдоль него плотности обусловливают его частичную фрагментацию.

6. РАСКРЫТИЕ ИНФОРМАЦИИ / DISCLOSURE

Автор заявляет об отсутствии какого-либо конфликта интересов. Автор прочел и одобрил финальную версию перед публикацией.

The author has no conflicts of interest to declare. The author read and approved the final manuscript.