Scroll to:
PROBLEMS OF NUMERICAL MODELING OF LARGE-SCALE MANTLE CONVECTION IN THE SUBDUCTION ZONE
https://doi.org/10.5800/GT-2024-15-6-0790
EDN: SZGWRF
Abstract
The article provides a review of modern models of large-scale mantle convection in the zone of a heavy cold oceanic plate (slab) subduction into the upper mantle. The formal approximation of the upper mantle for the present case is an incompressible Newtonian fluid with variable viscosity. It is assumed that the plate subduction is preceded by the stage of regime formation for thermo-gravitational convection in the mantle, which is caused by temperature and buoyancy of the lightweight hot substance. Important in this situation is the problem of quantitative formal modeling of phase transitions in the plate itself, as a result of which it becomes compacted due to thermal compression, removal of a part of lightweight mobile components of its original sediments and, consequently, overall weighting of the residual components of its material. It is also important to take into account the impact of mantle currents on the plate, which leads to its geometric distortion. Emphasis should also be placed on representing this plate/slab as an object of numerical modeling, since in the case of its representation as a thin elastic plate, adopted by Gustav Kirchhoff, the current hypotheses of normal remaining normal to the deformed middle surface of the plate and an unchanging thickness are violated.
The aim of the work is to construct a large-scale 2D numerical model of mantle convection in the subduction zone, which takes into account the thermal gravity regime for the upper mantle and the plate, initiated by plate subduction, the influence thereon of mantle flows (mantle wind), and phase transitions in the plate. Based on smoothed particles hydrodynamics (SPH), there was constructed a computational scheme of the slab dynamics. To verify the model, there have been performed a number of computational experiments, the results of which are generally consistent with the seismotomographically identified structure of mantle flows in the subduction zone. Thus, the model appears to show fragmentary nature of the process of subduction being due to the interaction between the subducting plate and the part that remains on the surface, which leads to deformation of the descending plate.
Keywords
For citations:
Chetyrbotsky A.N. PROBLEMS OF NUMERICAL MODELING OF LARGE-SCALE MANTLE CONVECTION IN THE SUBDUCTION ZONE. Geodynamics & Tectonophysics. 2024;15(6):0790. https://doi.org/10.5800/GT-2024-15-6-0790. EDN: SZGWRF
1. INTRODUCTION
In geodynamics, subduction is "the process by which an oceanic lithospheric plate/slab sinks into the mantle and moves under a continent or an island arc" [Stern, 2002, р. 5] where the main driving mechanisms of the Earth dynamics are thermal energy within the Earth [Khain, 2010] and density contrast between cold subducting plate and surrounding mantle. The reliability of this statement is confirmed by the fact that the mantle substance behaves as a solid at rapidly changing loads but can flow as a viscous fluid at long-term loads [Monin, 1977]. According to the theory of lithospheric plate tectonics, slab is a seismotomographically identified fragment of an 80–100 km thick oceanic lithospheric plate sinking (subducting) into the mantle [Koulakov et al., 2011; Sizova et al., 2014].
The importance of studying interaction between mantle convection and subduction lies in the understanding of the pattern of the distribution of substances in the geosphere and the structure and properties of the peripheral envelopes of the Earth. Subduction zones are one of the most tectonically active parts of the Earth related to large-scale mass and energy transport [Stern, 2002; Frost, 2006]. Of particular interest is the study of the processes in rheologically contrasting media: convective in relatively low-viscous asthenosphere and conductive in rigid lithosphere.
Though the numerical models of upper mantle convection have a wide coverage [Cristensen, 1984; Schubert, Anderson, 1985; Zhong, Gurnis, 1992; Dobretsov, Kirdyashkin, 1997; Lithgow-Bertelloni, Richards, 1997; Rychkova, Tychkov, 1997; Van Keken et al., 2011; Gerya, Yuen, 2003], there are still many open problems concerning changes in mantle convection structure induced by slab subduction; discontinuity and fragmentation of subduction; accumulation of slab material at the upper-lower mantle boundary; adaptation of modern computing methods for representation of upper mantle convection related to subduction zone. It is accepted that the lithosphere is entirely underlain by the asthenosphere whose viscosity is one or two orders of magnitude less than that of the lithosphere [Dobretsov et al., 2001]. But it is here that there are the conditions for melting of lithospheric material and generation of deep-focus earthquakes [Trubitsyn et al., 1993].
The aim of this work is the analysis of modern methods for solving some of the above-mentioned problems and the construction of 2D subduction dynamics models that take into account phase transitions in the subducting slab which cause a significant slab density increase. Consideration is being given to the schemes for solving nonlinear model equations and to the problems of software implementation of numerical modeling apparatus.
2. MANTLE CONVECTION AND SUBDUCTION MODELS
The study of subduction assumes that the character of interaction between mantle convection and slab is as follows. The lithospheric model description provided in [Zanemonets et al., 1974; Myasnikov, Markaryan, 1977; Bercovici et al., 1993] incudes highly viscous conductive quasi-fluid layer with zero velocity of fluid substance motion. The other part of the description consists of incompressible fluid whose rheological properties are characterized by the form for recording viscosity values and accepted initial and boundary conditions. Mantle flows usually assume constant slip at the computational area boundaries. However, conditions can arise for cyclic activation of magmatism at the asthenosphere-lithosphere boundary.
Mantle convection assumes to have chemical-dense nature [Keondzhyan, 1980; Monin, Sorokhtin, 1981]. Then, due to high viscosity, its modeling usually involves the Stokes equation in the Boussinesq approximation [Slezkin, 1955; Landau, Lifshits, 2001]. Accepting this approximation provides an opportunity to introduce the temperature factor into the equation for vorticity and, therefore, for velocity.
The tasks are solved for different forms of representation of viscosity. In terms of vorticity–stream function, heat convection was studied in viscosity continuum [McKenzie et al., 1974] and in the continuum where viscosity increases exponentially with depth [Gurnis, Davies, 1986].
A dynamic model of slab where it is represented by a negatively buoyant thin elastic plate is considered in [Turcotte, Schubert, 1985]. It is assumed that the plate bending is related to external vertical loads and ratios of its bending moments. Numerical model of subduction consists of the dimensionless equation for plate bending under the effect of applied moments and vertical loads. It is also assumed that a subducting plate can carry water deep into the upper mantle [Shubert et al., 2001]. This approach was adapted for the Amur microplate subduction through the upper mantle in [Gavrilov, Kharitonov, 2022], where phase transitions correspond to the key points in [Trubitsyn V.P., Trubitsyn A.P., 2014]. The eligibility of such approach is only limited by the first upper mantle layers where Kirchhoff’s hypothesis of normals remaining normal to the deformed middle surface of the plate and an unchanging plate thickness is applicable [Timoshenko, Woinowsky-Krieger, 1966]. However, the results of seismic sounding show that there is a decrease in the plate thickness [Fukao et al., 2009]. With plate subduction, there is a corresponding increase in pressure and temperature which leads to partial loss of light plate substance fractions, losses of water and gases from hydrous minerals and mineral lattice rearrangements, subsequent phase transitions, and slab fragmentation during deep subduction.
Alternative 2D models of upper mantle convection in the subduction zone are based on the statements of continuum mechanics and hydrodynamics where the equations of motion are expressed in the Stoke approximation [Gurnis, Davies, 1986; Doglioni et al., 2006; Van Keken et al., 2011; Duretz et al., 2012]. In these models, the process of subduction is mainly caused by excessive slab density. The mantle density follows the Boussinesq approximation. Some models differ in the form features of recording mantle and slab viscosity values, dependence of slab dynamics on temperature and tangential stress values [Van Keken et al., 2011], and in ways of impact on the plate and compositional variations [Kincaid, Sacks, 1997].
In [Gerya, Yuen, 2003], there is presented a 2D model of thermomechanical mantle convection in the Boussinesq approximation where the upper mantle viscosity is determined by temperature and pressure, and the model equations follow the Stokes approximation. Radioactivity and adiabatic and dissipative heating in the mantle act as independent spatiotemporal heat sources which determine the kinetics of slab subduction into the mantle. The computations are also based on using the marker and cell method. The solution is interpolated back to the Eulerian grid configuration at each time step. Such an approach requires considerable computational resources. Suffice to say that modeling of the Precambrian continental collision [Zakharov et al., 2015] was performed using the Lomonosov Moscow State University supercomputer complex.
In [Dobretsov, Kirdyashkin, 1997; Dobretsov et al., 2001, 2009; Koulakov et al., 2011], a study was made of thermophysical characteristics of only crustal layer which is a boundary layer between the mantle and the slab. However, these models do not consider the influence of mantle flows on slab dynamics.
In [Trubitsyn, 2008], consideration is being given to the case when the equation of temperature of the endothermic phase transition segment at the upper-lower mantle boundary is complemented by an analytic representation of a phase boundary shift/phase distribution function It is shown that an endothermic phase transition at a depth of 660 km does not lead to convection stratification. There has been observed slowdown and deformation of abnormally cold descending fluids. A slab model is a field of low temperature environment, and slab dynamics is determined by the same equations of mantle convection. The lack of a slab model as a representation of a real object of the upper mantle – slab system may be due to the drawback of this approach.
In [Bobrov, Baranov, 2014], the viscosity ratio considers deformation plasticity which results in abrupt mode of subduction and abrupt changes in stress fields depending on the slab separation stage. In the areas which do not contain subducting slabs the stresses are very low. The overall picture for temperature dynamics shows the slab segments as dense isothermal patterns. The lack of a slab model as a representation of a real object of the upper mantle – slab system may be due to the drawback of this approach.
In [Lobkovskii, Ramazanov, 2021], Galerkin method application and Fourier series expansion provide a basis for an analytical representation of a stationary solution to model equations of convection in the mantle whose substance is determined by a cold fluid. There are presented the results of computational experiments for structural variations in convective cells depending on the Rayleigh number. The lack of a slab model as a representation of a real object of the upper mantle – slab system therein may also be due to the drawback of this approach.
The above-mentioned publications do not consider the problems of transformation of hydrous minerals of the slab that occurs due to squeezing water out of the upper mantle rocks. Besides, in many cases the slab is not regarded as an independent geodynamic object.
3. SLAB FORMATION AND SUBDUCTION DYNAMICS
A model of mantle dynamics in the subduction zone consists of interrelated systems of equations, the first of which determines mantle dynamics, and the second – a colder and a denser oceanic plate subduction against the background of the converted mantle. The mantle is modeled by a two-dimensional incompressible Newton fluid in the Cartesian coordinate system. Due to high viscosity of the mantle, the quasi-stationary two-dimensional convective fluids are determined by the well-known Stoke equations, whose dimensionless form in terms of vorticity – stream function is derived as [Torrance, Turcotte, 1971; Turcotte, Schubert, 2002]:
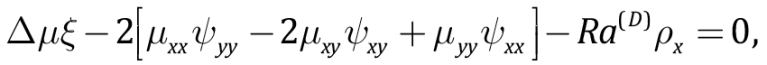 (1)
(1)
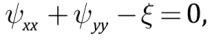 (2)
(2)
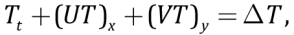 (3)
(3)
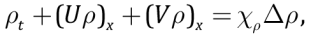 (4)
(4)
where dimensionless variables stand for: x, y – axes of the Cartesian coordinate system (x=y=0 left corner), y-axis is directed downward;
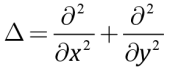 – 2D Laplace operator;
– 2D Laplace operator;
μ(T,y), ξ(x,y,t), ψ(x,y,t), ρ(x,y,t) – dynamic viscosity of the mantle, vorticity, stream function of mantle flow and mantle density; U(x,y,t)=ψy, V(x,y,t)=–ψx, T(x,y,t) – lateral and vertical velocities of mantle flow, temperature distribution in the mantle;
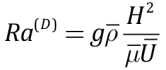 – the Rayleigh number for upper mantle;
– the Rayleigh number for upper mantle;
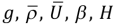 – gravitational acceleration, typical densities and velocities of mantle flows, coefficient of thermal expansion and upper mantle depth; dT=Tmax–Tmin – drop in temperature typical of the upper mantle; χρ – diffusion coefficient as a function of density for rocks; lower indices of the variables show at the corresponding partial derivatives of the same name.
– gravitational acceleration, typical densities and velocities of mantle flows, coefficient of thermal expansion and upper mantle depth; dT=Tmax–Tmin – drop in temperature typical of the upper mantle; χρ – diffusion coefficient as a function of density for rocks; lower indices of the variables show at the corresponding partial derivatives of the same name.
The velocity-vorticity relation (1) allows avoiding the obvious presence of pressure.
Nondimensionalization of (1)–(3) was performed in a standard way (the primes denote dimensionless variables):
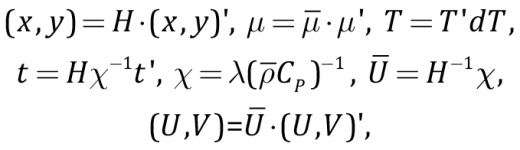
where the variables with upper bars are typical values; λ and χ are thermal conductivity and thermal diffusivity of the mantle, and СР is isobaric specific heat capacity; the subsequent dimensionless equations omit the primes.
The computational domain is a two-dimensional rectangular region of the Cartesian coordinate system. The boundary conditions imply the absence of heatflow and substance on the lateral faces of the computational domain and the presence of heatflow and substance on the upper gT,0, gρ,0 and lower gT,H, gρ,H faces of the domain:
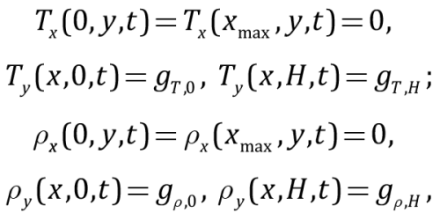 (5)
(5)
where xmax is a dimensionless lateral extent.
Stream function assumes no-slip condition on the lateral extents: ψ(0,y,t)=ψ(xmax,y,t)=0, ψn(0,y,t)=ψn(xmax,y,t)=0, where n is a normal [Lobkovsky et al., 2013, 2021]. The portion of the upper mantle where an oceanic plate moves towards the subduction zone, as well as the entire bottom of the mantle, assume slip condition:

when y=0, interval X is a horizontal portion of the upper mantle where the plate moves towards its subduction zone, and when y=1, interval X is lateral component x; at solid boundaries (including the boundaries with the slab), stream function is equal to zero; the vorticity value is determined by Thom’s formula [Roache, 1980]
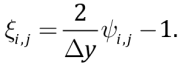 (6)
(6)
Analysis of seismotomographic profiles [Stern, 2002; Fukao et al., 2009] shows that the extension of the slab is much greater than the thickness which allows providing its model representation via a flexible thin bar and implies the independence of horizontal subduction velocity on vertical y coordinate and that of vertical subduction velocity on x coordinate. It is also assumed that the slab is in hydrostatic state, and the slab density can be calculated from the density of the mixture of heavy ρH=const and light ρL=const components (solid solution). The slab subduction occurs at ρ*–ρ˃0. Then the subduction model can be determined by the following dimensionless equations
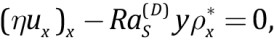 (7)
(7)
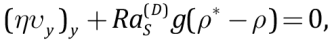 (8)
(8)
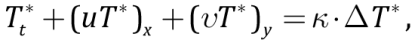 (9)
(9)
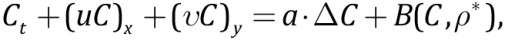 (10)
(10)
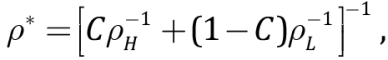 (11)
(11)
where η(T,y) is slab viscosity about 1021–1023 H·s/m2 [Kirdyashkin A.A., Kirdyashkin A.G., 2023]); u(x,t), v(y,t), T*(x,y,t), ρ*(x,y,t) – are horizontal and vertical velocities of slab subduction, slab temperature and slab density; y is a dimensionless vertical coordinate; к is temperature diffusion coefficient for the slab;
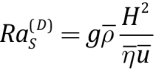 is the Rayleigh number for the slab;
is the Rayleigh number for the slab;
C(x,y,t) is heavy component concentration in the slab; B(C,ρ*) determines dynamics of partial phase transformations of the slab substance due to ascent or removal of its light components.
The B(C,ρ*) formulation set forth herein assumes the following. Seawater seeps into oceanic lithosphere through fractures and pores, and reacts with minerals in the crust and mantle to form hydrous minerals (such as serpentine) that store water in their crystal structures [Turcotte, Schubert, 1985]. That is why during the slab subduction, there are various transformations of such minerals (in particular, the formation of more compacted units of minerals due water squeezing) which can be interpreted as a partial phase transition of the slab substance. In this situation, large amounts of gas- and water-saturated formations (fluids) accumulate at the mantle – slab boundary [Dobretsov et al., 2017], which subsequently can cause seismicity and partial melting of the subducting slab substance [Gerya et al., 2004]. Then, during the slab subduction, there is an increase in pressure and temperature of a medium which causes a removal/ascent of a light component, resulting in an increase in heavy component concentration and a subsequent weighting of the slab substance. The mechanism of this process is as follow. At early stages of subduction of the slab, when its substance is oversaturated with seawater (and, consequently, light components) seeped therein, an increase in pressure and temperature of a medium promotes an intensive ascent and a subsequent formation of excess volumes of high-temperature and gas-saturated components. Before the slab density becomes similar to the density of the medium, the slab subduction slows down, thus forming stagnant areas of accumulation of the slab substance. The fact is that the effect of mantle flow and an irregular distribution of the slab density lead to a difference in stresses and subsequent deformations thereon and, finally, to slab fragmentation. There is so called slab stagnation whose boundaries are clearly defined along the hypocenters of deep-focus earthquakes. Their maximum recorded depth, particularly under South America and Central America, does not exceed 700 km [Stern, 2002; Fukao et al., 2009]. Then, with an increase in heavy component concentration in the slab, there is a break of the stagnation zone, with a subsequent subduction of the fragments down to the Earth’s core [Agrusta et al., 2017].
A simple record of such mechanism herein is determined by relation:
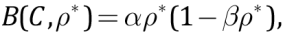 (12)
(12)
where α, β are nonnegative parameters of a model. The right part (12) is a well-known logistic function [Svirizhev, Logofet, 1978], attaining its maximum at ρ**=(2β)–1. The applicability of (12) for the slab density dynamics could be as follows. At the stage up to ρ**, there is a linear growth of heavy component concentration, and after this stage is over the growth in heavy component concentration is sharp.
The upper-mantle boundary condition for subduction model (6)–(10) is determined by an initial segment of subduction where typical subduction velocity is assigned. At the upper mantle bottom there is an accumulation of the slab substance.
Seismic tomography of the upper mantle shows the mantle – slab boundary irregularities which are mainly due to the influence of mantle flow on the slab. The thickness of the slab therewith is much less than the extension, which allows providing its model representation via a flexible and thin bar, affected by the mantle flow. In this situation, the need for getting partial derivatives to solve (7)–(10) in a curvilinear coordinate system with dynamic and irregular boundaries allows the use of adequate meshfree methods. Here it is appropriate to use the Lagrangian meshfree particle method (SPH) [Monaghan, 2005]. This method is based on representation of the object of study (slab herein) as a finite set of elements/particles [Harlow, 1967], carrying density, spatial location and velocity properties, and as a set of additional attributes.
The essence of the method lies in the fact that a certain physical characteristic 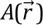 of a single particle in point
of a single particle in point 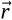 is determined by the weighted sum of this value for other particles
is determined by the weighted sum of this value for other particles
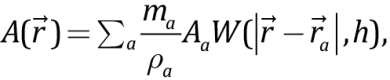 (13)
(13)
which lie in neighborhood 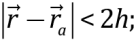 are mass and density of the particle with number а,
are mass and density of the particle with number а, 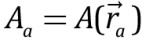 and h (so called smoothing length);
and h (so called smoothing length); 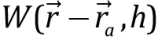 is an analytic kernel through which the particle properties are smoothed and their mutual influences are taken into account. The smoothing function determines the amount of impact of each particle on the calculated value. As the particle, for which the attribute value is calculated, is closer to a nearby particle, the effect of the latter on the result becomes more pronounced, and the smoothing function increases more rapidly is this position [Aliev, 2008; Medin, Parshikov, 2010]. In this situation, the calculation of partial derivatives
is an analytic kernel through which the particle properties are smoothed and their mutual influences are taken into account. The smoothing function determines the amount of impact of each particle on the calculated value. As the particle, for which the attribute value is calculated, is closer to a nearby particle, the effect of the latter on the result becomes more pronounced, and the smoothing function increases more rapidly is this position [Aliev, 2008; Medin, Parshikov, 2010]. In this situation, the calculation of partial derivatives
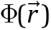 comes down to their calculation for analytic function:
comes down to their calculation for analytic function:

where b, a are ordinal numbers of particles, b, a=1÷N(t); N(t) – is the current amount of particles in the method; xba=xb–xa, yba=yb–ya and 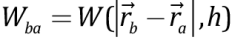 – is kernel function which provides the basis for analytical calculations of the derivatives set in square brackets. The Laplacian of
– is kernel function which provides the basis for analytical calculations of the derivatives set in square brackets. The Laplacian of 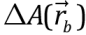 is provided after [Brookshaw, 1985]. For the kernel function use has been made of the 3rd degree spline curve
is provided after [Brookshaw, 1985]. For the kernel function use has been made of the 3rd degree spline curve
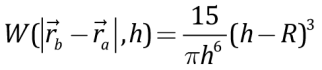 at 0<R<h,
at 0<R<h,
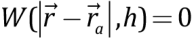 at R>h;
at R>h;
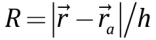
[Monaghan, 2005].
With the SPH method the heat transfer formula for the bth particle is given by
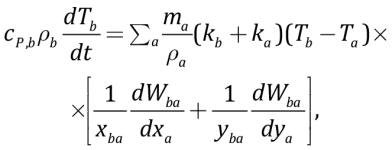 (14)
(14)
where cP,b, Tb, Ta, kb, ka, xa, ya are heat capacity, temperature, thermal conductivity coefficient and coordinates for corresponding particles. For t+1 moment, they are determined by:
 (15)
(15)
where 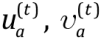 are lateral and vertical particle velocities determined by the SPH method from (7) and (8) with the given initial and boundary conditions.
are lateral and vertical particle velocities determined by the SPH method from (7) and (8) with the given initial and boundary conditions.
4. COMPUTATIONAL EXPERIMENTS
A regular computational grid:
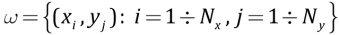
is generated as follows: xi=xi–1+dx, yi=yi–1+dy where dx and dy are step sizes along the axes; Nx and Ny are the amounts of steps along the coordinate axes; a dimensionless temporal step dt is assumed const. The pressure is assumed to be hydrostatic, and the relationship between dimensionless viscosity for the upper mantle and slab is derived as:
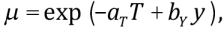
where aT=–0.2 and bY=1.33 [Trubitsyn et al., 1993; Bobrov, Baranov, 2014].
Initial distributions for temperature and density follow equations:
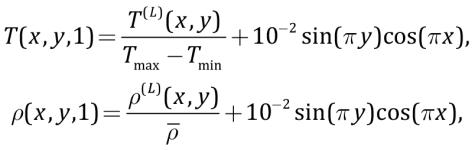
where T(L)(x,y) and ρ(L)(x,y) were derived based on the sources referred to herein [Dziewonski, Anderson, 1981; Rychkova, Tychkov, 1997; Sorokhtin, Ushakov, 2002; Honda, Yuen, 1994].
The study of the structural transformation of mantle convection in the subduction zone was performed using the following numerical values of the parameters involved in the calculations: Nx=100, Ny=50, dt=10–4, dτ=10–6, Δx=9.67∙10–2, Δy=5.76∙10–2.
Time interval 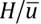 is 9.1324∙107 years (
is 9.1324∙107 years (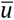 is the typical scale of the slab subduction velocity). Number of time intervals Nt=2000 and time step Δt=4.132∙104 years.
is the typical scale of the slab subduction velocity). Number of time intervals Nt=2000 and time step Δt=4.132∙104 years.
For the upper mantle, the numerical values of model parameters in (1)–(4) were obtained based on [Dobretsov, Kirdyashkin, 1997; Dobretsov et al., 2001, 2009; Dobretsov, 2010; Stern, 2002; Kirdyashkin et al., 2002; Royden, Husson, 2009; Kirdyashkin A.A., Kirdyashkin A.G., 2023]. In particular, the following values were assumed:
L=6.7·106 m, H=7·105 m, g=9.8 m·s–2,
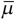 =1022 P,
=1022 P,
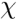 =2.88·10–7 m2·s–1,
=2.88·10–7 m2·s–1,
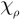 =2·10–8 m2·s–1,
=2·10–8 m2·s–1,
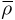 =3.808·103 kg·m–3,
=3.808·103 kg·m–3,
cP =1.2·103 J·kg–1K–1,
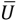 =10–13 m·s–1,
=10–13 m·s–1,
Ra(D) =1.866·107.
The subduction model parameters were chosen with regard to slab dehydrotation in accordance with (10), and density variations within the slab follow (11). In order to assume these relations for the entire mantle, it should be taken into account that the slab attains its maximum density at the core-mantle boundary [Fukao et al., 2009]. Dehydratation and decrease in viscosity of the subducting substance trigger exhumation of high-baric rocks [Reverddato et al., 2022]. The parameter values for the subduction model (6)–(10) are set equal to:
ρН=5.607·103 kg·m–3, ρL=103 kg·m–3,
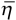 =1023 P,
=1023 P,
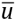 =1.6·10–9 m·s–1,
=1.6·10–9 m·s–1,
к=4.608·10–3 m2·s–1, α=2, β=0.8433,
where ρН, α and β were determined through computational experiments.
Numerical values of particle attributes are randomly determined based on the following variable ranges in model (7)–(11): velocity – 5–8 cm/yr; temperature – 1000–1500 °С; density – 3500–3600 kg/m3; heavy component concentration was calculated using formula (11) by substituting density value into its left part. These ranges were set based on [Dobretsov et al., 2001, 2009; Dobretsov, 2010; Kirdyashkin et al., 2000, 2002; Royden, Husson, 2009; Kirdyashkin A.A., Kirdyashkin A.G., 2023].
Numerical solution for the equations of both systems, (1–2) and (7–8), was obtained based on the pseudo-stationary method which consists in creating an equivalent non-stationary task and in subsequent task solving by the march method (task solution in partial derivatives under assigned initial and boundary conditions) until a stationary state is reached in which time step dτ acts as an iteration parameter [Fletcher, 1991]. Since the Courant-Friedrichs-Lewy condition (U/Δx2+V/Δy2)dt for solving the system of equations is much less than 1, then equations (3–4) and (8–9) are solved using explicit difference schemes.
The computational algorithm is as follows. First, the mantle convection regime is set up for a computational domain with the initial and boundary conditions (5) through which equations (1)–(4) are solved using a regular grid. The stream function for the mantle – slab boundary is equal to zero, and the vorticity value follows (6). The solution of (7)–(11) is obtained as follows. For the segment of slab sinking into the mantle (computational cell (xA,1) there is obtained a set of particles with definite characteristics such as velocity, temperature, and density. In order to avoid the particle concentration on this segment, this set is activated only in case of lack of particles therein. Then the particle dynamics follows equations (7)–(15). The effect of mantle flow on subduction dynamics is taken into account in supplementing the slab model with sets of identical particles from the adjacent mantle cells.
A model of mantle convection in the subduction zone after 500 temporal iterations (more than 4 million years) is shown in Fig. 1 where large dots indicate the coordinates of the slab segments (to aid the visualization, the scale of stream function is hereinafter increased by 1000 times).
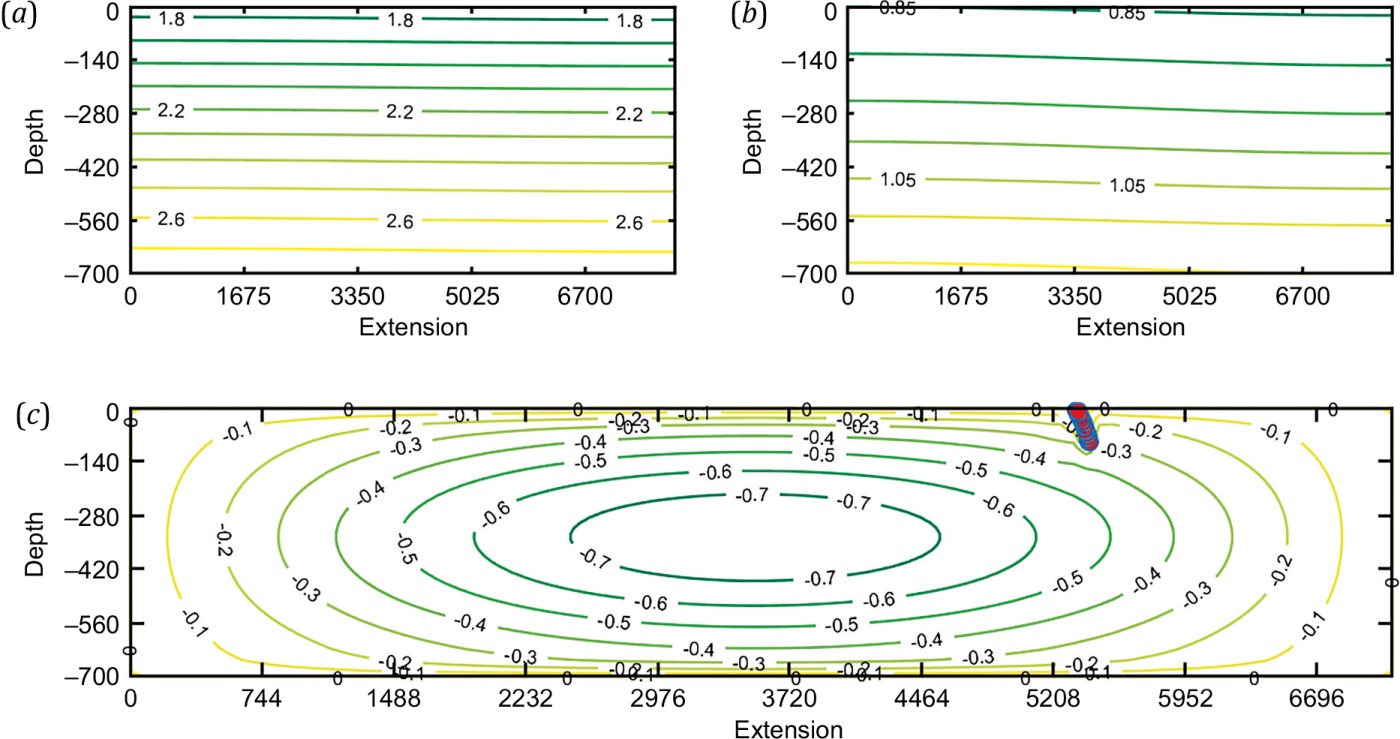
Fig. 1. Distribution of temperature (a), density (b), and allocation of stream function and slab configuration (c) after 500 steps of calculations.
Analysis of Fig. 1 shows the smooth flow where the stream function values in the cell center are seven times higher than those at the domain boundaries. There is a slight variation in heat and mass transfer components due to the balance of their flows between the geospheres. Under the statement of the problem, no-slip condition is fulfilled and the stream function is equal to zero on the domain boundary. Since the mantle – slab boundary is impermeable, the stream function also turns to zero thereon which causes smooth flowing around the slab profile.
The distribution of temperature T, density ρ and stream function ψ after 1500 temporal iterations (more than 48 million years) is shown in Fig. 2. For convenience and clarity, the dynamics of the spatiotemporal distributions of temperature and density is presented as deviations from corresponding values for t=500.
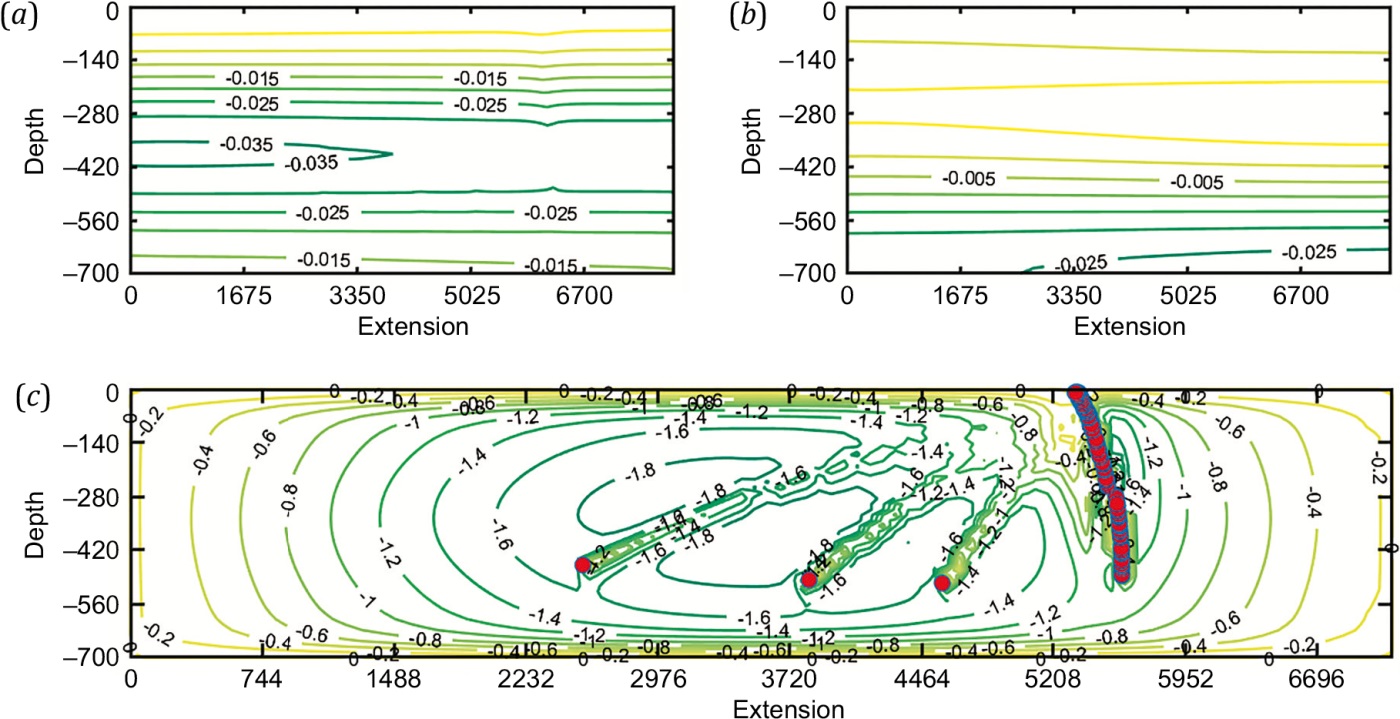
Fig. 2. Distribution of temperature (a), density (b), and allocation of stream function and slab configuration (c) after 1500 steps of calculations.
The comparison between temperature and density for different temporal iterations shows some cooling and softening of the bottom layers in the upper mantle which is assumably due to non-zero flows of heat and substance at the upper mantle boundaries (condition (5)). The analysis of Fig. 2, b, shows somewhat non-linear density distribution: between the layers with negative density deviation for dimensionless t=500, there is a layer with positive density deviation. This is caused by convective mixing in the mantle. Also of note are temporal evolution of the stream function and, therefore, the impact on the slab which gives rise to the occurrence of different deformations in the slab body and subsequently leads to its partial fragmentation.
The distribution of temperature, density and streamlines after 1900 temporal iterations (more than 91million years) is shown in Fig. 3.
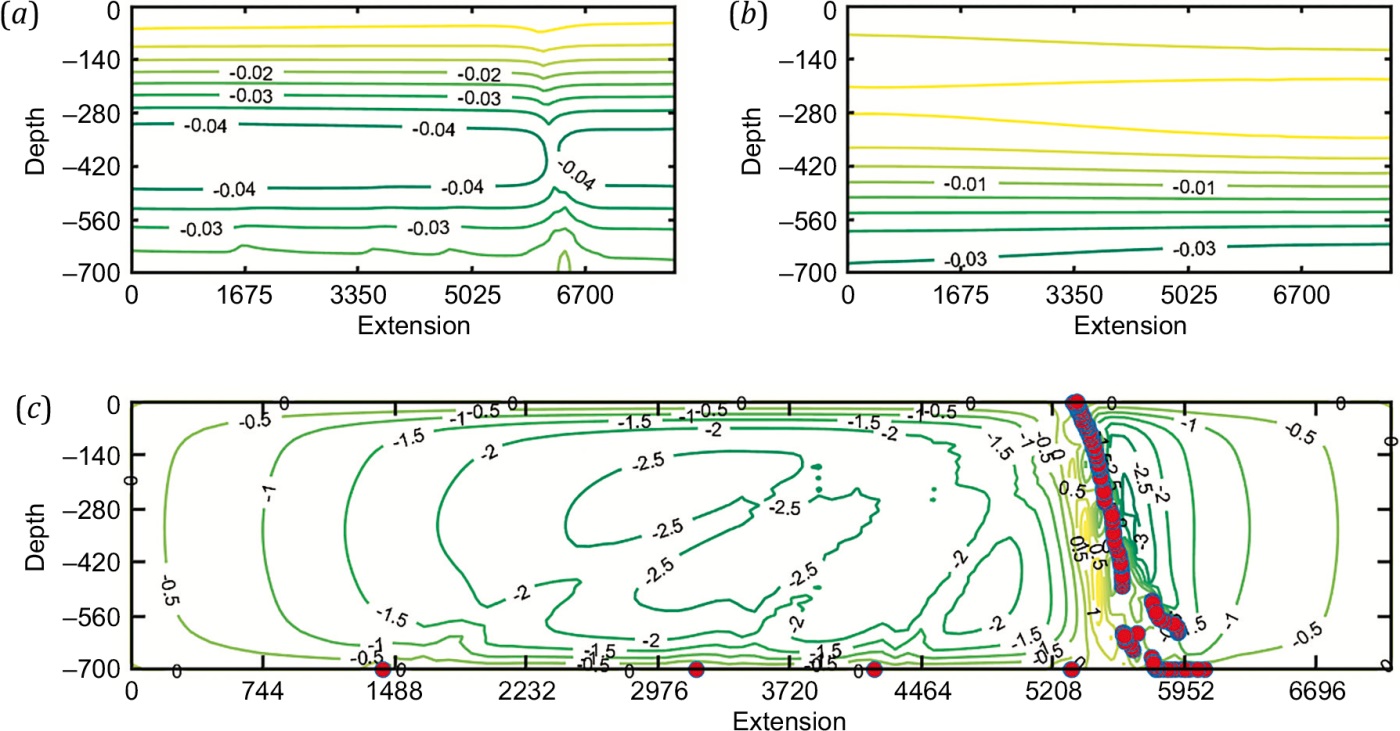
Fig. 3. Distribution of temperature (a), density (b), and allocation of stream function and slab configuration (c) after 1900 steps of calculations.
The distribution of temperature shows some cooling of the bottom layers in the upper mantle which is attributed to the heat efflux. Also of note is some softening of the bottom layers due to convective mixing. As a result of plate sinking into the mantle (subduction), the initial convective cell is split into two components. The slab therein acts as a real vertical "partition". The distribution pattern of isolines in Fig. 2, c, and Fig. 3, c, shows that in the immediate vicinity of the slab there are conditions for the compaction of the stream function values and the formation of small-scale (Karig) vortices [Gavrilov, Kharitonov, 2017]).
As the slab approaches the bottom of the lower mantle, it appears to be flattening out which is due to an increase in its temperature and decrease in its viscosity therein. Together with denser underlying layers, this leads to deformation of the frontal part of the slab under the effect of convective flows.
The manifestation of features of the formation of small-scale vortices, as well as that of flattening out and fragmentation of the slab, becomes illustrative in the scaled neighborhood of the slab in Fig. 4.
The effect of mantle flows on the slab and an irregular density distribution thereon cause its partial fragmentation. The slab fragments reach the top of the lower mantle and accumulate there (diffusion of particles at this boundary is assumable).
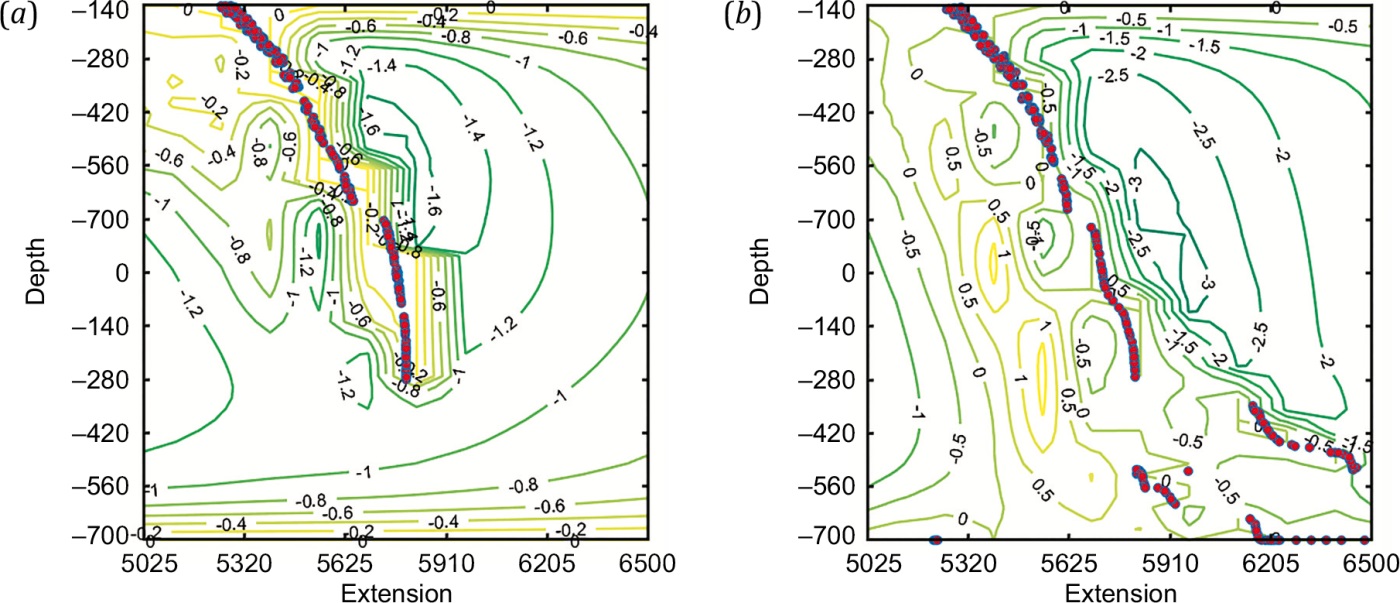
Fig. 4. Scaled neighborhood of the slab configuration after 1500 (a) and 1900 (b) steps of calculations.
5. CONCLUSION
The paper deals with the key principles for modeling subduction in the upper mantle. Consideration is being given to a complex model consisting of a model of mantle convection (vorticity equations, stream functions, heat and mass transfer equations) and a spatiotemporal model of slab dynamics (velocity equations, heat and mass transfer equations, adapted SPH method for solving the problem). The paper proposes a model for quantitative accounting of phase transitions in the slab substance.
The effect of mantle flows on the subduction dynamics is taken into account by supplementing the slab model with the sets of identical particles from the slab-adjacent mantle cells.
The effect of mantle flows on the slab and an irregular density distribution thereon causes its partial fragmentation.
6. DISCLOSURE
The author has no conflicts of interest to declare. The author read and approved the final manuscript.
References
1. Agrusta R., Goes S., van Humen J., 2017. Subducting-Slab Transition-Zone Interaction: Stagnant, Penetration and Mode Switch. Earth and Planetary Science Letters 464, 10–23. https://doi.org/10.1016/j.epsl.2017.02.005.
2. Aliev A.V., 2008. Application of the Smoothed Particle Hydrodynamics Method for Solving Gas-Dynamic Problems. Numerical Methods and Programming 9, 40–47 (in Russian)
3. Bercovici D., Sсhubert G., Tackley P.J., 1993. On the Penetration of the 660 km Phase Change by Mantle Downflows. Geophysical Research Letters 20 (23), 2599–2602. https://doi.org/10.1029/93GL02691.
4. Bobrov A.M., Baranov A.A., 2014. The Structure of Mantle Flows and Stress Fields in a Two-Dimensional Convection Model with Non-Newtonian Viscosity. Russian Geology and Geophysics 55 (7), 801–811. https://doi.org/10.1016/j.rgg.2014.06.001.
5. Brookshaw L., 1985. A Method of Calculating Radiative Heat Diffusion in Particle Simulations. Proceedings of the Astronomical Society of Australia 6 (2), 207–210. https://doi.org/10.1017/S1323358000018117.
6. Cristensen U., 1984. Convection with Pressure- and Temperature-Depend Non Newtonian Rheology. Geophysical Journal International 77 (2), 343–384. https://doi.org/10.1111/j.1365-246X.1984.tb01939.x.
7. Dobretsov N.L., 2010. Distinctive Petrological, Geochemical, and Geodynamic Features of Subduction-Related Magmatism. Petrology 18, 84–106. https://doi.org/10.1134/S0869591110010042.
8. Dobretsov N.L., Kirdyashkin A.G., 1997. Modeling of Subduction Processes. Russian Geology and Geophysics 38 (5), 846–856 (in Russian)
9. Dobretsov N.L., Kirdyashkin A.G., Kirdyashkin A.A., 2001. Deep Geodynamics. GEO, Novosibirsk, 409 p. (in Russian)
10. Dobretsov N.L., Kirdyashkin A.G., Kirdyashkin A.A., 2009. Geodynamic and Thermal Models of a Subduction Zone. Physical Mesomechanics 12 (1), 5–16 (in Russian)
11. Dobretsov N.L., Simonov V.A., Koulakov I.Yu., Kotlyarov A.V., 2017. Migration of Fluids and Melts in Subduction Zones and General Aspects of Thermophysical Modeling in Geology. Russian Geology and Geophysics 58 (5), 571–585. https://doi.org/10.1016/j.rgg.2016.09.028.
12. Doglioni C., Cuffaro M., Carminati E., 2006. What Moves Slabs? Bollettino di Geofisica Teorica ed Applicata 47 (3), 227–247.
13. Duretz T., Gerya T.V., Kaus J.P., Andersen T.B., 2012. Thermomechanical Modeling of Slab Eduction. Journal of Geophysical Research: Solid Earth 117, B8. https://doi.org/10.1029/2012JB009137.
14. Dziewonski A.M., Anderson D.L., 1981. Preliminary Reference Earth Model. Physics of the Earth and Planetary Interiors 25 (4), 277–356. https://doi.org/10.1016/0031-9201(81)90046-7.
15. Fletcher С.A.J., 1991. Computational Techniques for Fluid Dynamics. Vol. 2. Mir, Moscow, 552 p. (in Russian)
16. Frost D.J., 2006. The Stability of Hydrous Mantle Phases. Reviews in Mineralogy and Geochemistry 62 (1), 243–271. https://doi.org/10.2138/rmg.2006.62.11.
17. Fukao Y., Obayashi M., Nakakuki M., Deep Slab Project Group, 2009. Stagnant Slab: A Review. Annual Review of Earth and Planetary Sciences 37, 19–46. https://doi.org/10.1146/annurev.earth.36.031207.124224.
18. Gavrilov S.V., Kharitonov A.L., 2017. On Karig Convective Rolls within the Mantle Wedge beneath the Timan-Pechora Plate as the Mechanism of Transport of the Hydrocarbons at Paleozoic. Vestnik of the Institute of Geology of the Komi Science Centre of the Ural Branch of the Russian Academy of Sciences 8, 12–16 (in Russian) https://doi.org/10.19110/2221-1381-2017-8-12-16.
19. Gavrilov S.V., Kharitonov A.L., 2022. On the Subduction of the Amur Microplate and the Convective Mechanism of the Removal of Dissipative Heat and Hydrocarbons from the Mantle Wedge in the Sea of Okhotsk East of Sakhalin Island. Herald of the Academy of Sciences of the Republic of Bashkortostan 42 (1), 5–12 (in Russian) https://doi.org/10.24412/1728-5283_2022_1_5_12.
20. Gerya T.V., Yuen D.A., 2003. Characteristics-Based Marker-in-Cell Method with Conservative Finite-Differences Schemes for Modeling Geological Flows with Strongly Variable Transport Properties. Physics of the Earth and Planetary Interiors 140 (3), 293–318. https://doi.org/10.1016/j.pepi.2003.09.006.
21. Gerya T.V., Yuen D.A., Meresch W.V., 2004. Thermomechanical Modelling of Slab Detachment. Earth and Planetary Science Letters 226 (1–2), 101–116. https://doi.org/10.1016/j.epsl.2004.07.022.
22. Gurnis M., Davies G.F., 1986. Numerical Study of High Rayleigh Number Convection in a Medium with Depth-Depend Viscosity. Geophysical Journal International 85 (3), 523–541. https://doi.org/10.1111/j.1365-246X.1986.tb04530.x.
23. Harlow F.H., 1967. The Particle-in-Cell Computing Method for Fluid Dynamics. In: B. Alder, S. Fernbach, M. Rotenberg (Eds), Computational Methods in Hydrodynamics. Mir, Moscow, p. 316–342 (in Russian)
24. Honda S., Yuen D.A., 1994. Model for Convective Cooling of Mantle with Phase Changes: Effects of Aspect Ratios and Initial Conditions. Journal of Physics of the Earth 42 (2), 165–186. https://doi.org/10.4294/jpe1952.42.165.
25. Keondzhyan V.N., 1980. A Model of Chemical-Density Differentiation of the Earth’s Mantle. Physics of the Earth 8, 3–15 (in Russian)
26. Khain V.E., 2010. Constructing a Truly Global Model of Earth’s Dynamics: Basic Principles. Geology and Geophysics 51 (6), 587–591. https://doi.org/10.1016/j.rgg.2010.05.001.
27. Kincaid C., Sacks I.S., 1997. Thermal and Dynamical Evolution of the Upper Mantle in Subduction Zones. Journal of Geophysical Research: Solid Earth 102 (B6), 12295–12315. https://doi.org/10.1029/96JB03553.
28. Kirdyashkin A.A., Dobretsov N.L., Kirdyashkin A.G., 2002. Experimental Modeling of the Influence of Subduction on the Spatial Structure of Convection Currents in the Asthenosphere under Continents. Doklady Earth Sciences 385 (5), 546–550.
29. Kirdyashkin A.A., Kirdyashkin A.G., 2023. Temperature Distribution in a Subducting Plate and in the Upper Mantle at the Continental Limb of the Subduction Zone. Geosphere Research 1, 6–19 (in Russian) DOI:10.17223/25421379/26/1.
30. Kirdyashkin A.A., Kirdyashkin A.G., Dobretsov N.L., 2000. Influence of Subduction on the Structure of Thermal Gravitational Flows in the Asthenosphere under the Continent. Russian Geology and Geophysics 41 (2), 207–219 (in Russian)
31. Koulakov I.Yu., Dobretsov N.L., Bushenkova N.A., Yakovlev A.V., 2011. Slab Shape in Subduction Zones beneath the Kurile-Kamchatka and Aleutian Arcs Based on Regional Tomography Results. Russian Geology and Geophysics 52 (6), 650–667. https://doi.org/10.1016/j.rgg.2011.05.008.
32. Landau L.D., Lifshits E.M., 2001. Theoretical Physics. Vol. VI. Hydrodynamics. Fizmatlit, Moscow, 736 p. (in Russian)
33. Lithgow-Bertelloni C., Richards M., 1998. The Dynamics of Cenozoic and Mesozoic Plate Motions. Reviews of Geophysics 36 (1), 27–78. https://doi.org/10.1029/97RG02282.
34. Lobkovskii L.I., Ramazanov M.M., 2021. Investigation of Convection in the Upper Mantle Connected Thermomechanically with the Subduction Zone and Its Geodynamic Application to the Arctic Region and North East Asia. Fluid Dynamics 56, 433–444. https://doi.org/10.1134/S001546282103006X.
35. Lobkovsky L.I., Kononov M.V., Shipilov E.V., 2013. Geodynamic Model of Upper Mantle Convection and Transformations of the Arctic Lithosphere in the Mesozoic and Cenozoic. Izvestiya, Physics of the Solid Earth 49, 767-785. https://doi.org/10.1134/S1069351313060104.
36. Lobkovsky L.I., Ramazanov M.M., Kotelkin V.D., 2021. Convection Related to Subduction Zone and Application of the Model to Investigate the Cretaceous-Cenozoic Geodynamics of Central East Asia and the Arctic. Geodynamics & Tectonophysics 12 (3), 455–470 (in Russian) https://doi.org/10.5800/GT-2021-12-3-0533.
37. McKenzie D.P., Roberts J.M., Weiss N.O., 1974. Convection in the Earth’s Mantle: Towards a Numerical Simulation. Journal of Fluid Mechanics 62 (3), 465–538. https://doi.org/10.1017/S0022112074000784.
38. Medin S.A., Parshikov A.N., 2010. Development of Smoothed Particle Hydrodynamics Method and Its Application in the Hydrodynamics of Condensed Matter. High Temperature 48, 926–933. https://doi.org/10.1134/S0018151X10060210.
39. Monaghan J.J., 2005. Smoothed Particle Hydrodynamics. Reports on Progress in Physics 68 (8), 1703. https://doi.org/10.1088/0034-4885/68/8/R01.
40. Monin A.N., 1977. History of the Earth. Nauka, Leningrad, 228 p. (in Russian)
41. Monin A.N., Sorokhtin O.G., 1981. On the Earth’s Volumetric Gravity Differentiation. Doklady of the USSR Academy of Sciences 259 (5), 1076–1079 (in Russian)
42. Myasnikov V.P., Makaryan E.G., 1977. Geodynamic Model of the Earth’s Evolution. Doklady of the USSR Academy of Sciences 237 (5), 1055–1058 (in Russian)
43. Reverdatto V.V., Polyansky O.P., Semenov A.N., Babichev A.V., 2022. Mathematical Modeling of the Mechanism of Continental Subduction. Doklady Earth Sciences 503. 179–184. https://doi.org/10.1134/S1028334X22040158.
44. Roache P.J., 1980. Computational Fluid Dynamics. Mir, Moscow, 618 p. (in Russian)
45. Royden L.H., Husson L., 2009. Subduction with Variations in Slab Buoyancy: Models and Application to the Banda and Apennine Systems. In: S. Lallemand, F. Funiciello (Eds), Subduction Zone Geodynamics. Springer, Berlin, Heidelberg, p. 35–46. https://doi.org/10.1007/978-3-540-87974-9_2.
46. Rychkova H.V., Tychkov S.A., 1997. Numerical Model of Thermal Convection in the Upper Mantle of the Earth under Continental Lithosphere. Computational Technologies 5 (2), 66–81 (in Russian)
47. Schubert G., Anderson C.A., 1985. Finite Element Calculation of Very High Rayleigh Number Thermal Convection. Geophysical Journal International 80 (3), 575–601. https://doi.org/10.1111/j.1365-246X.1985.tb05112.x.
48. Schubert G., Turcotte D.L., Olson P., 2001. Mantle Convection in the Earth and Planets. Cambridge University Press, New York, 958 p. https://doi.org/10.1017/CBO9780511612879.
49. Sizova E.V., Gerya T.V., Brown M., 2014. Contrasting Styles of Phanerozoic and Precambrian Continental Collision. Gondwana Research 25 (2), 522–545. https://doi.org/10.1016/j.gr.2012.12.011.
50. Slezkin N.A., 1955. Dynamics of Incompressible Viscous Fluid. Gostekhizdat, Moscow, 521 p. (in Russian)
51. Sorokhtin O.G., Ushakov S.A., 2002. The Evolution of the Earth. Textbook. MSU Publishing House, Moscow, 506 p. (in Russian)
52. Stern R.J., 2002. Subduction Zones. Reviews of Geophysics 40 (4), 3-1–3-38. https://doi.org/10.1029/2001RG000108.
53. Svirezhev Yu.M., Logofet D.O., 1978. Stability of Biological Communities. Nauka, Moscow, 352 p. (in Russian)
54. Timoshenko S., Woinowsky-Krieger S., 1966. Theory of Plates and Shells. Second Ed. Nauka, Moscow, 636 p. (in Russian)
55. Torrance K.E., Turcotte D.L., 1971. Thermal Convection with Large Viscosity Variations. Journal of Fluid Mechanics 47 (1), 113–125. https://doi.org/10.1017/S002211207100096X.
56. Trubitsyn V.P., 2008. Seismic Tomography and Continental Drift. Izvestiya, Physics of the Solid Earth 44, 857–872. https://doi.org/10.1134/S1069351308110013.
57. Trubitsyn V.P., Belavina Yu.F., Rykov V.V., 1993. Thermal and Mechanical Interaction of the Mantle with the Continental Lithosphere. Physics of the Earth 11, 3–15 (in Russian)
58. Trubitsyn V.P., Trubitsyn A.P., 2014. Numerical Model for the Generation of the Ensemble of Lithospheric Plates and Their Penetration through the 660-km Boundary. Izvestiya, Physics of the Solid Earth 50, 853–864. https://doi.org/10.7868/S0002333714060106.
59. Turcotte D.L., Schubert G., 1985. Geodynamics. Applications of Continuum Physics to Geological Problems. Part 1. Mir, Moscow, 376 p. (in Russian)
60. Turcotte D.L., Schubert G., 2002. Geodynamics. Cambridge University Press, New York, 456 p.
61. Van Keken P.E., Hacker B.R., Syracuse E.M., Abers G.A., 2011. Subduction Factory: 4. Depth-Dependent Flux of H2O from Subducting Slabs Worldwide. Journal of Geophysical Research: Solid Earth 116, B1. https://doi.org/10.1029/2010JB007922.
62. Zakharov V.S., Perchuk A.L., Zav’yalov S.P., Sineva T.A., Gerya T.V., 2015. Supercomputer Simulation of Continental Collisions in Precambrian: the Effect of Lithosphere Thickness. Moscow University Geology Bulletin 70 (2), 77–83. https://doi.org/10.3103/S014587521502012X.
63. Zanemonets V.B., Kotelkin V.D., Myasnikov V.P., 1974. On Lithospheric Dynamics. Bulletin of the USSR Academy of Sciences. Physics of the Earth 5, 43–54 (in Russian)
64. Zhong S., Gurnis M., 1992. Viscous Flow Model of a Subduction Zone with a Faulted Lithosphere: Long and Short Wavelength Topography, Gravity and Geoid. Geophysical Research Letters 19 (18), 1891–1894. https://doi.org/10.1029/92GL02142.
About the Author
A. N. ChetyrbotskyRussian Federation
159 100-letya Ave, Vladivostok 690022
Review
For citations:
Chetyrbotsky A.N. PROBLEMS OF NUMERICAL MODELING OF LARGE-SCALE MANTLE CONVECTION IN THE SUBDUCTION ZONE. Geodynamics & Tectonophysics. 2024;15(6):0790. https://doi.org/10.5800/GT-2024-15-6-0790. EDN: SZGWRF



















































