Перейти к:
РАСПРЕДЕЛЕНИЕ ПРИВЕДЕННОЙ СЕЙСМИЧЕСКОЙ ЭНЕРГИИ И СБРОШЕННЫХ НАПРЯЖЕНИЙ В АЛТАЕ-САЯНСКОМ СЕЙСМОАКТИВНОМ РЕГИОНЕ
https://doi.org/10.5800/GT-2025-16-4-0835
EDN: VWPTKO
Аннотация
Для Алтае-Саянского сейсмоактивного региона сформирован банк данных по тензорам сейсмического момента землетрясений, произошедших в 1978–2025 гг. Для этих событий скалярный сейсмический момент M0 уже известен по СМТ-каталогу. В данной работе проведены оценки таких динамических параметров, как радиус очага r, сброс касательных напряжений Δσ, приведенной сейсмической энергии ePR с использованием феноменологического подхода, основанного на ранее полученных регрессионных соотношениях между радиусом очага и скалярным сейсмическим моментом M0. Получены оценки сброшенных напряжений и приведенной сейсмической энергии для 69 землетрясений с магнитудой MW от 3.5 до 7.2. Тем самым существенно расширен банк данных по этим параметрам землетрясений Алтае-Саянского сейсмоактивного региона. Построены карты распределения по площади усредненных значений сброшенных напряжений и приведенной сейсмической энергии.
Ключевые слова
Для цитирования:
Сычева Н.А., Богомолов Л.М. РАСПРЕДЕЛЕНИЕ ПРИВЕДЕННОЙ СЕЙСМИЧЕСКОЙ ЭНЕРГИИ И СБРОШЕННЫХ НАПРЯЖЕНИЙ В АЛТАЕ-САЯНСКОМ СЕЙСМОАКТИВНОМ РЕГИОНЕ. Геодинамика и тектонофизика. 2025;16(4):0835. https://doi.org/10.5800/GT-2025-16-4-0835. EDN: VWPTKO
For citation:
Sycheva N.A., Bogomolov L.M. DISTRIBUTION OF REDUCED SEISMIC ENERGY AND STRESS DROP IN THE ALTAI-SAYAN SEISMOACTIVE REGION. Geodynamics & Tectonophysics. 2025;16(4):0835. https://doi.org/10.5800/GT-2025-16-4-0835. EDN: VWPTKO
ВВЕДЕНИЕ
Разработка новых подходов к прогнозированию разрушительных землетрясений и уменьшению их последствий включает, по необходимости, расширение объема данных о динамических параметрах: радиусе очага землетрясения r, скалярном сейсмическом моменте M0 и сбросе касательных напряжений, действующих параллельно плоскости разрыва. Далее для краткости будем использовать термин «сброшенные напряжения» (stress drop, ∆σ). Информация об этих параметрах, непосредственно относящихся к объемам очагов землетрясений, а также о приведенной сейсмической энергии (отношение сейсмической энергии ES к сейсмическому моменту: ePR=ES/M0) может характеризовать региональные особенности геодеформационного процесса. Поле напряжений в земной коре является одним из основных факторов, учитываемых при оценках магнитуды прогнозируемого землетрясения. Тектонические особенности, такие как разломы, складчатость, трещины и вулканы, являются результатом воздействия напряжений. Падение напряжения в очагах землетрясений является ключевым параметром, который позволяет оценить, какая часть накопленной энергии высвобождается землетрясением. Кроме того, изменение со временем усредненных сброшенных напряжений для событий заданных магнитуд отражает напряженное состояние земной коры на диаграмме Кулона – Мора. Для такого описания земной коры сейсмоактивных регионов необходим статистически значимый набор данных – достаточно большое число сейсмических событий, для которых определены динамические параметры очагов. Также представляет интерес сопоставление распределений кинематических (фокальных) параметров очагов и сейсмотектонических деформаций (СТД) с динамическими параметрами. Отметим, что кинематические и динамические параметры очагов землетрясений совместно естественно называть очаговыми, хотя в некоторых работах под «очаговыми» параметрами подразумеваются только динамические [Sycheva, Bogomolov, 2016].
Как известно, для определения динамических параметров землетрясений необходимо построить очаговый спектр их сейсмограмм, по которому определяются спектральная плотность Ω0 (вклад наиболее низкочастотных гармоник) и угловая частота f0 (параметр, описывающий убывание амплитуды высокочастотных гармоник). По найденным значениям Ω0 можно рассчитать скалярный сейсмический момент по известной формуле [Riznichenko, 1985], описывающей пропорциональность M0~Ω0, причем коэффициент пропорциональности определяется только параметрами среды в области очага. А полученные данные об угловой частоте позволяют оценить радиус очага (r~1/f0) с точностью до коэффициента, зависящего от модели подвижки в очаге (так как существуют модели излучения сейсмических волн) [Riznichenko, 1985; Scholz, 2002]. Наиболее известны модели Брюна, Мадариаги и др. (обзор в [Sycheva, Bogomolov, 2020]). Для таких расчетов скалярного сейсмического момента и радиуса очага существенно то, что M0 не зависит от угловой частоты f0, а Ω0 не влияет на радиус r.
Для вычисления сброшенных напряжений можно использовать выражение [Kostrov, 1975; Scholz, 2002]:
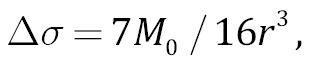 (1)
(1)
указывающее на то, что значение ∆σ пропорционально произведению Ω0 f03~M0 f03. Из-за этого погрешность при оценке угловой частоты и радиуса очага приводит к существенно большей погрешности ∆σ. Согласно модели разрыва в очаге [Madariaga, 2011], величину приведенной сейсмической энергии можно оценить по формуле:
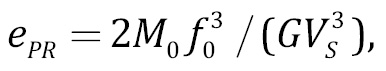 (2)
(2)
где G – модуль сдвига пород, залегающих в области очага, VS – скорость поперечных волн (G=ρVS2, ρ – плотность). Поскольку r~1/f0, величины сброшенных напряжений и приведенной сейсмической энергии оказываются пропорциональны друг другу [Kocharyan, 2016]. Для перехода от значений ∆σ к значениям ePR можно использовать пересчетную формулу [Sycheva, Bogomolov, 2020]:
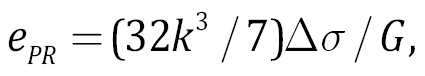 (3)
(3)
где k – численный коэффициент, зависящий от модели очага и равный k=0.37 для модели Брюна [Brune, 1970, 1971] и k=0.26 для усовершенствованной модели Мадариаги – Канеко – Ширера [Kaneko, Shearer, 2014]. Важно отметить, что приведенная сейсмическая энергия, в отличие от сброшенных напряжений, не зависит от выбора модели очага, как это следует из (2). А в выражении (3) произведение k3∆σ оказывается одинаковым для моделей Брюна, Мадариаги – Канеко – Ширера и др., поскольку ∆σ~1/r3~1/k3 [Sycheva, Bogomolov, 2020].
В работах [Kocharyan, 2014, 2016] обосновано, что в случае, когда значения ePR статистически независимы от сейсмического момента M0, имеет место самоподобие сейсмических очагов, а при наличии регрессии (аппроксимирующей зависимости ePR от M0) самоподобие отсутствует. В связи с этим представляет интерес массовое определение значений сброшенных напряжений и/или приведенной сейсмической энергии. Для Северного Тянь-Шаня результаты такого исследования представлены в обобщении [Sycheva et al., 2020]. На примере этого региона была отработана методика расчетов динамических параметров для очагов землетрясений (с магнитудой 2.60–5.35, одно землетрясение имело магнитуду М=6, Кочкорское, 25.12.2006 г.). Составной частью этой работы является переход от станционного спектра сейсмограмм к очаговому спектру, для чего необходима информация о добротности среды. Как следствие, задача расчета сброшенных напряжений требует высокого качества сейсмических записей и значительных вычислительных ресурсов для определения спектральных параметров Ω0 и f0. При этом погрешность при определении угловой частоты часто оказывается большей, чем при определении параметра Ω0, из-за чего в публикациях чаще приводятся выходные данные лишь по сейсмическому моменту M0.
Если рассматривать землетрясения, для которых известен скалярный сейсмический момент (источник данных описан ниже), то для оценочных расчетов сброшенных напряжений и приведенной сейсмической энергии можно попытаться использовать регрессионные зависимости радиуса очага от энергетической характеристики (M0, или моментной магнитуды MW). Подразумевается использование модельных зависимостей (регрессий), которые были предложены в работах, обобщающих данные по динамическим параметрам в рассматриваемом или в других регионах, или же обоснованы теоретически. В настоящей работе для оценок значений ∆σ и ePR землетрясений на территории Алтае-Саянской горной области применен такой подход.
Целью является создание (расширение) банка данных по всем динамическим параметрам на основе данных о 69 землетрясениях с известным сейсмическим моментом, произошедших в изучаемом регионе в период 1978–2025 гг. Для выбора подходящей аппроксимационной зависимости радиуса очага от моментной магнитуды рассмотрены различные регрессии, полученные в работах [Riznichenko, 1985; Dobrynina, 2009; Zavyalov, Zotov, 2021; Kim et al., 1989; Boore, 2003; Bormann et al., 2009; Sycheva, Bogomolov, 2020]. С учетом особенностей этих регрессий, различающихся по диапазону MW, построена усредненная модель зависимости радиуса очага от энергетической характеристики события.
Алтае-Саянское нагорье – область активного горообразования, продолжающегося и в наши дни, свидетельством чему служат многочисленные сильные землетрясения современности. Как показывает анализ современной кинематики литосферных блоков в Центральной Азии [Sankov et al., 2002; Abdrakhmatov et al., 1996; Larson et al., 1999], коллизия Индостана и Евразии определяет лишь ту часть внутриконтинентальных деформаций, которая локализуется западнее 105-го меридиана.
На рис. 1 представлено эпицентральное положение землетрясений, из каталога ФИЦ ЕГС РАН (http://www.gsras.ru/) по региону Алтай и Саяны, которые произошли с 1997 по 2021 г. Станции Алтае-Саянского филиала ФИЦ ЕГС РАН позволяют регистрировать землетрясения, произошедшие не только в Алтае-Саянской горной области, но и на территории ближайшего окружения – в Восточном Казахстане, Монгольском Алтае, в северной части Монголии и Южном Прибайкалье. На эту же карту вынесены эпицентры крупных землетрясений, произошедших на этой территории с 1761 г. с магнитудой М≥6 (рис. 1). На рис. 1 обозначены границы блоков согласно [Sankov et al., 2003]. Основная часть крупных землетрясений произошла на границе блоков [Emanov et al., 2023]. Значительная часть этих землетрясений происходила вблизи границ Тувино-Монгольского блока [Emanov et al., 2023]. В структуре сейсмичности выделяется сейсмически активизированная блоковая структура, охватывающая Тувино-Монгольский блок совместно с восточной частью Тувинского нагорья [Emanov et al., 2023].
Уникальный афтершоковый процесс сформировался после Бусийнгольского землетрясения 1991 г. Возник пульсирующий режим с кратковременной активизацией около одного месяца, повторяющийся на протяжении более двадцати лет. Смена режима произошла на уровне 2010 г., но сейсмическая активность данной эпицентральной зоны не затихает по сей день. Тувинские землетрясения 2011–2012 гг. [Emanov et al., 2014a] произошли в зоне Каахемского разлома в асейсмичном за инструментальный период районе [Emanov et al., 2023]. Сформировалась очаговая область двух близких по энергии землетрясений как единая структура с высокой активностью до настоящего времени. К северу от очага Бусийнгольского землетрясения 1991 г. сейсмическая активность усилилась в горном обрамлении рифтовой впадины Белинской [Emanov et al., 2010, 2014b, 2021]. При исследованиях сейсмичности Прихубсугулья отмечалось изменение напряженного состояния в этом районе относительно впадин байкальского типа [Misharina et al., 1983], а также было указано, что сейсмичность Хубсугульской впадины не соответствует ее строению и тектоническому положению [Logachev, 1993], что предвосхитило сейсмическую активизацию 2021 г. [Emanov et al., 2022]. После 2021 г. отмечается повышенная активность вдоль граней всей блочной структуры. Принципиально новым является возникновение Дархатского роя землетрясений в месте, где прежде сейсмичность не наблюдалась. С 1963 г. на данном участке землетрясений не было. События происходили уже после Хубсугульского землетрясения 2021 г. Прежде сейсмически активная осевая линия Дархатской впадины и активизация не затрагивали территорию развития роя землетрясений. Рой землетрясений возник в выступе котловины на восток в центральной части, в месте изгиба горного хребта, разделяющего Дархатскую и Хубсугульскую впадины.
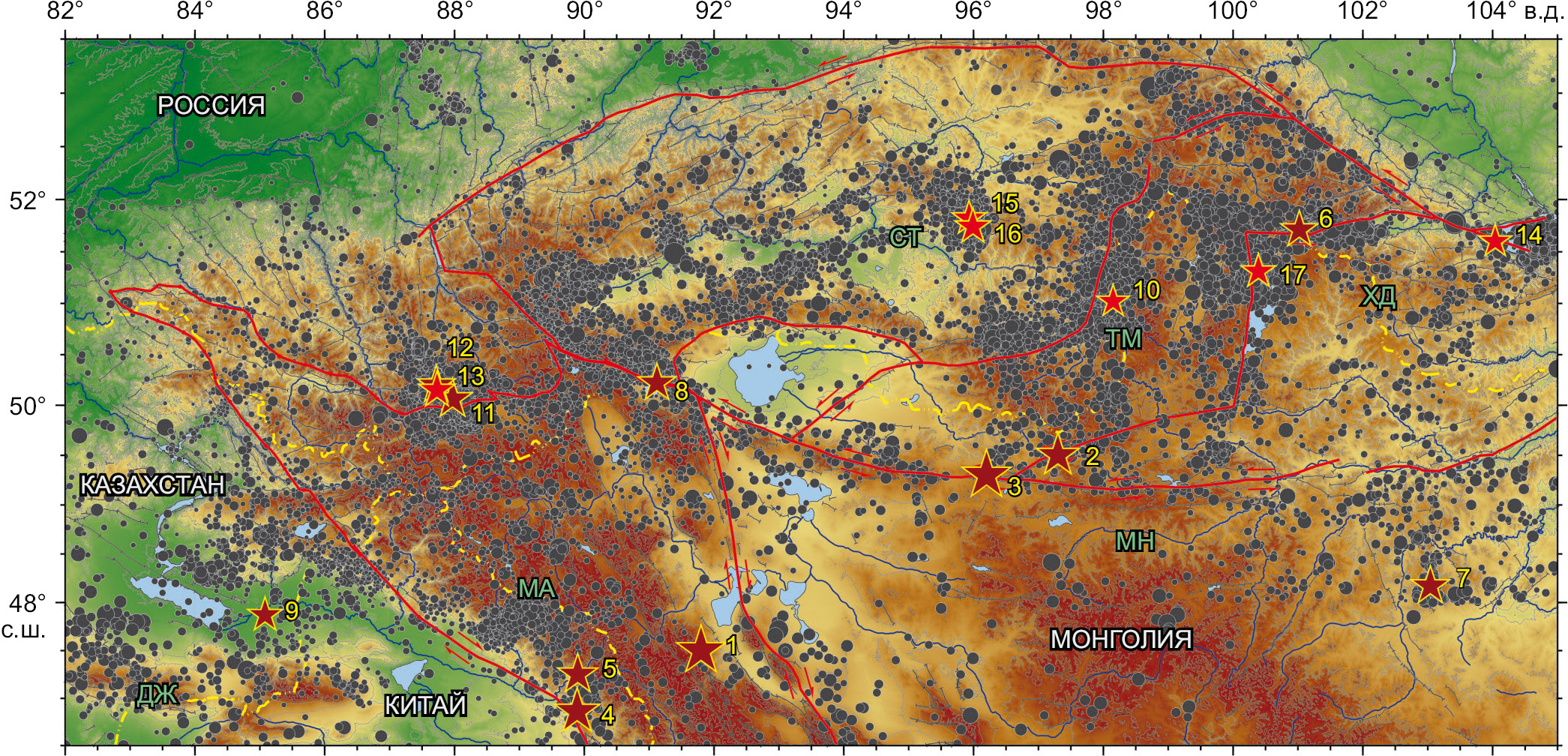
Рис. 1. Эпицентральное положение землетрясений Алтае-Саянской горной области (из каталога ЕГС РАН, более 22000 событий, 1997–2021 гг.).
Звездочками обозначены сильные землетрясения: красный цвет – с М≥6, темно-красный – с М≥7. Желтым цветом обозначены номера землетрясений: 1 – Великое Монгольское, 1761 г., М=8.3; 2 – Танну-Ольское, 1905 г., М=7.6; 3 – Болнайское, 1905 г., М=8.3; 4 – Фуюньское, 1931 г., М=7.9; 5 – афтершок Фуюньского, 1931 г., М=7.3; 6 – Мондинское, 1950 г., М=7.0; 7 – Могодское, 1967 г., М=7.0; 8 – Урэг-Нурское, 1970 г., М=7.0; 9 – Зайсанское, 1990 г., М=6.8; 10 – Бусийнгольское, 1991 г., М=6.4; 11 – Чуйское, 2003 г., М=7.3; 12 – афтершок Чуйского, 2003 г., М=7.0; 13 – афтершок Чуйского, 2003 г., М=6.9; 14 – Култукское, 2008 г., М=6.4; 15 – Тувинское I, 2011 г., М=6.6; 16 – Тувинское II, 2012 г., М=6.8; 17 – Хубсугульское, 2021 г., М=6.9. Буквами обозначены блоки [Sankov et al., 2003]: СТ – Саяно-Тувинский, ТМ – Тувино-Монгольский, ХД – Хамар-Дабанский, МА – Монголо-Алтайский, ДЖ – Джунгарский, МН – Монгольский.
Fig. 1. Epicentral location of earthquakes in the Altai-Sayan mountain region (from the catalogue of the GS RAS, over 22000 events, 1997–2021).
Stars mark strong earthquakes: red – M≥6 earthquakes; dark red – with M≥7 earthquakes. Earthquake numbers are shown in yellow: 1 – Great Mongolian, 1761, M=8.3; 2 – Tannu-Ola, 1905, M=7.6; 3 – Bolnai, 1905, M=8.3; 4 – Fuyun, 1931, M=7.9; 5 – aftershock of the Fuyun earthquake, 1931, M=7.3; 6 – Mondy, 1950, M=7.0; 7 – Mogod, 1967, M=7.0; 8 – Ureg-Nur, 1970, M=7.0; 9 – Zaysan, 1990, M=6.8; 10 – Busingol, 1991, M=6.4; 11 – Chuya, 2003, M=7.3; 12 – aftershock of the Chuya earthquake, 2003, M=7.0; 13 – aftershock of the Chuya earthquake, 2003, M=6.9; 14 – Kultuk, 2008, M=6.4; 15 – Tuva I, 2011, M=6.6; 16 – Tuva II, 2012, M=6.8; 17 – Khubsugul, 2021, M=6.9. Letters indicate blocks [Sankov et al., 2003]: СT – Sayan-Tuva, TM – Tuva-Mongolian, ХД – Khamar Daban, MA – Mongolian Altai, ДЖ – Dzungar, MH – Mongolian.
ИСХОДНЫЕ ДАННЫЕ И МЕТОДИКА
В качестве исходных данных рассматриваются землетрясения, произошедшие на территории Алтае-Саянской горной области и ближайшего окружения, для которых рассчитан скалярный сейсмический момент. Источником таких данных является каталог СМТ (Centroid Moment Tensor, https://www.globalcmt.org/CMTsearch.html). Указанный источник, наряду с компонентами тензора сейсмического момента, включает скалярный сейсмический момент М0 и моментную магнитуду MW. Эти параметры были получены для 66 землетрясений, произошедших в Алтае-Саянской горной области с 1978 по 2025 г. На рис. 2 представлены тензоры сейсмического момента этих землетрясений. К 66 событиям из каталога СМТ (рис. 2) нами добавлено три землетрясения за 2003 г. (афтершоки Чуйского землетрясения) из каталога ЕГС РАН, для которых определена моментная магнитуда и скалярный сейсмический момент, что увеличило количество рассматриваемых событий до 69. На рис. 2 эпицентральное положение этих землетрясений отмечено синим цветом. Тензоры сейсмического момента (каталог СМТ) и эпицентры трех землетрясений (каталог ФИЦ ЕГС РАН) представлены на фоне распределения количества землетрясений в год, рассчитанного на основе данных, показанных на рис. 1 (землетрясения из каталога ФИЦ ЕГС РАН с 1997 по 2021 г.). Расчет количественного распределения землетрясений проводился в ячейках размером 1×1° (объем данных более 22000 событий позволяет рассматривать территорию ~100×100 км), при этом рассматривалась только представительная часть каталога землетрясений (2≤М≤7.3 [Sycheva, Sychev, 2022]). Темно-зеленым цветом отмечены ячейки с числом землетрясений в год N>15. Максимальное количество землетрясений в год (73 события) отмечено в ячейке с центром 50.5° с.ш. и 87.5° в.д. (очаговая область Чуйского землетрясения, 2003 г.), задание верхней границы легенды (N=73) привело бы к отображению только одной зоны – области Чуйского землетрясения. Значительная часть рассматриваемых землетрясений (69 событий) лежит в ячейках с высоким уровнем сейсмичности.
Некоторые количественные характеристики 69 землетрясений представлены на рис. 3: моментная магнитуда землетрясений варьируется в диапазоне 4.0–7.2, значительная часть событий (68 %) имеет магнитуду MW=4.75–5.50 (рис. 3, а), основная часть землетрясений произошла после 2000 г. (рис. 3, б), и максимум событий приходится на 2003 г. (Чуйское землетрясение и его афтершоки). Землетрясения произошли на глубине 10–35 км, для трех землетрясений, добавленных из каталога ЕГС РАН, глубина не определена. Этим событиям присвоена глубина 15 км (рис. 3, в), как это сделано в работе [Kuchai, 2012], где анализируются фокальные механизмы землетрясений Алтая и Саян и отмечено, что из-за отсутствия надежного определения глубин очагов в Алтае-Саянской горной области глубина землетрясений принималась равной 15 км.
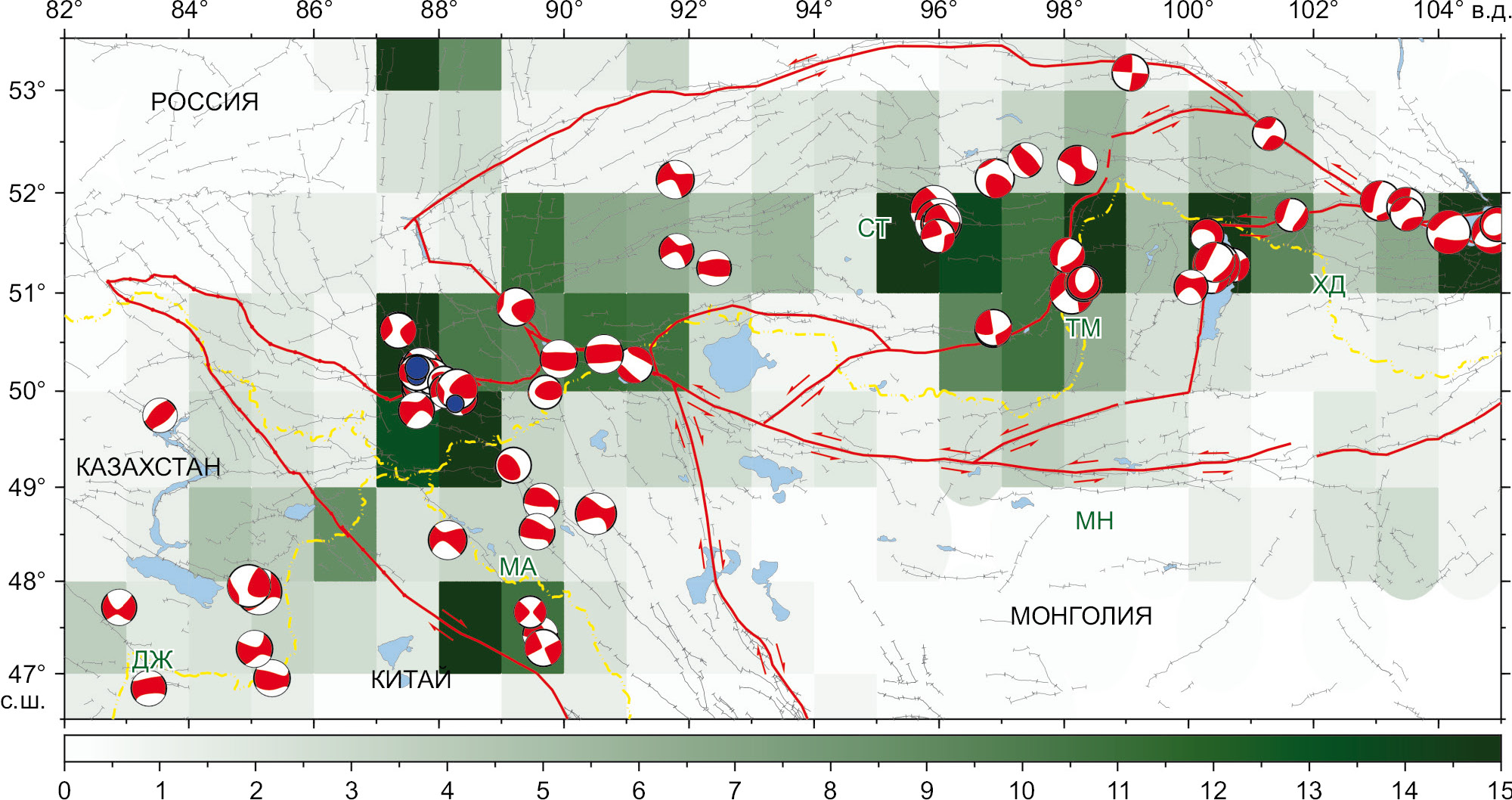
Рис. 2. Тензоры сейсмического момента (СМТ) для землетрясений Алтая, Саян и ближайшего окружения (66 событий) на фоне количества землетрясений в год (из каталога ЕГС РАН, более 22000 событий, 1997–2021 гг.).
Серые линии – разломы из работы [Bachmanov et al., 2017]. Штрихпунктирная линия – государственная граница. Синим цветом отмечены эпицентры землетрясений (3 события) из каталога ЕГС РАН, для которых известен скалярный сейсмический момент. Названия блоков см. рис. 1.
Fig. 2. Seismic moment tensors (СMT) for the earthquakes in the Altai, Sayan and adjacent areas (66 events) against the background of the annual earthquake number (more than 22000 events from 1997 to 2021 in the GS RAS catalog).
Gray lines are faults after [Bachmanov et al., 2017]. The dash-dotted line is the state border. Blue color stands for the epicenters of the earthquakes (3 events) from the GS RAS catalog for which the scalar seismic moment is known. See Fig. 1 for the block names.
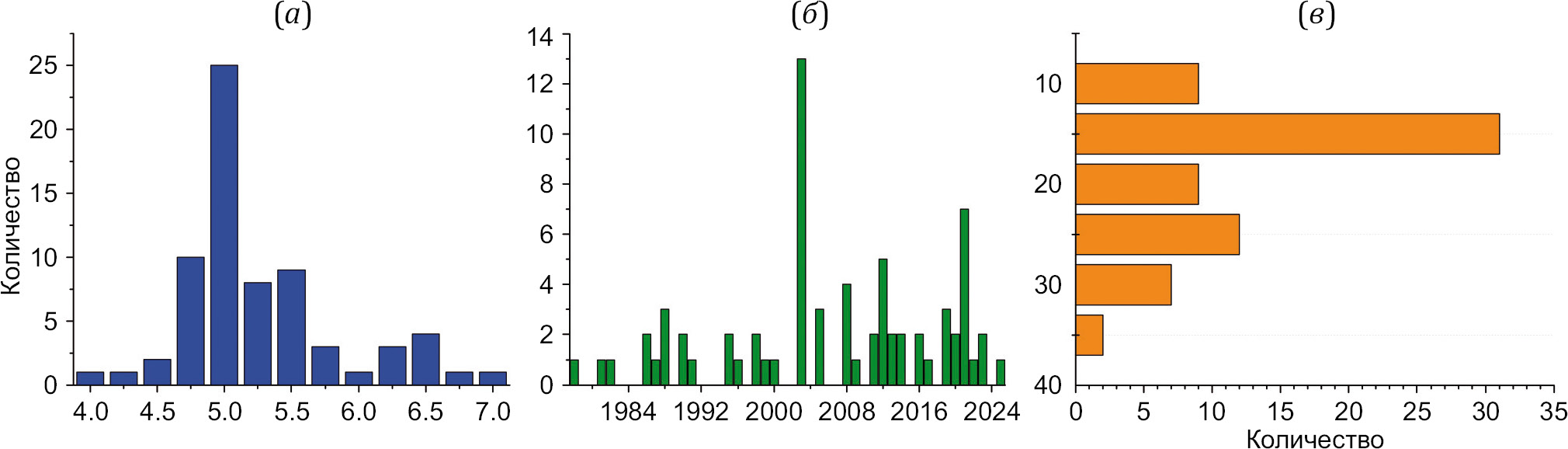
Рис. 3. Количественное распределение рассматриваемых землетрясений (69 событий): (а) – по магнитуде, (б) – по годам, (в) – по глубине.
Fig. 3. Quantitative distribution of the earthquakes under consideration (69 events): (a) – by magnitude, (б) – by year, (в) – by depth.
Для выбора модели, связывающей радиус очага с магнитудой MW, рассмотрим примеры регрессий из работ по исследованию динамических параметров, цитированных выше во Введении. Установленные в этих работах зависимости r(MW) сведены в табл. 1, где также приведены характеристики, указывающие на особенности каждой модели.
В работе [Bormann et al., 2009] представлены спектры амплитуд смещения грунта A для среднего источника сейсмического сдвига в зависимости от частоты f, масштабированные по сейсмическому моменту M0 и эквивалентной моментной величине MW. Отмечено, что максимум сейсмической энергии ES излучается в районе угловой частоты fc, которая указана в работе для каждого значения моментной магнитуды начиная от 4.5 до 9 с шагом 0.5. На основе этих данных рассчитан радиус очага для модели Брюна [Brune, 1970, 1971], построено распределение радиуса очага от моментной магнитуды и определено уравнение регрессии для событий с MW≥4.5.
В теоретической работе [Boore, 2003] представлен простой и мощный метод моделирования движений грунта, который состоит в сочетании параметрического или функционального описания амплитудного спектра колебаний грунта со случайным фазовым спектром, модифицированным таким образом, что движение распределяется по продолжительности, связанной с магнитудой землетрясения и расстоянием от источника. Этот простой метод оказался успешным при сопоставлении различных показателей движения грунта при землетрясениях с сейсмическим моментом более 12 порядков величины (что соответствует землетрясениям с MW>2.5) и в различных тектонических средах.
В обобщении [Riznichenko, 1985, с. 32] при составлении зависимости радиуса очага от магнитуды и класса землетрясения приведены результаты работ [Chinnery, 1961, 1969; и др.], посвященных анализу сильных землетрясений. В недавней работе [Zavyalov, Zotov, 2021], посвященной выявлению наиболее общих свойств во взаимосвязи характерного размера очага землетрясения с его магнитудой, получена регрессионная зависимость, практически совпадающая с результатом из статьи [Riznichenko, 1985] в диапазоне магнитуд 5.5–8.5.
В работах [Sycheva, Bogomolov, 2020; Dobrynina, 2009; Kim et al., 1989] рассматриваются динамические параметры землетрясений, произошедших в различных регионах: Северном Тянь-Шане, Байкальской рифтовой зоне и на Балтийском щите соответственно. В работе [Vakov, 1988] показано, что для нормальных коровых землетрясений, происходивших вне зон Беньоффа-Заварицкого, соотношения между их магнитудами и размерами очага определяются в основном типом подвижки и мало зависят от региональных условий, что позволяет нам рассматривать работы по динамическим параметрам землетрясений по разным регионам. В этих работах анализировались события, большинство из которых являются слабыми (диапазон магнитуд для каждого региона указан в табл. 1). Лишь единичные события имели моментную магнитуду выше 5. А вот в теоретических работах предложены зависимости радиуса очага для землетрясений в широком диапазоне магнитуд, включая сильнейшие события табл. 1, поэтому выбор модели или способ их объединения являются весьма нетривиальными. На рис. 4, а, показаны зависимости логарифма радиуса очага от моментной магнитуды, согласно источникам из табл. 1. Каждая из модельных регрессий показана в границах магнитуд, для которых она была определена. Важно отметить близость графиков для модели [Bormann et al., 2009] и моделей [Riznichenko, 1985; Zavyalov, Zotov, 2021] в диапазоне магнитуд 4.5<MW<8. Наличие такого соответствия весьма нетривиально, поскольку в работе [Bormann et al., 2009] радиус очага (радиус Брюна) определяется по параметрам спектра смещения и характеризует излучение сейсмических волн, а подход [Zavyalov, Zotov, 2021] основан на анализе распределения гипоцентров афтершоков и дает оценку размера разрыва, получившегося уже после главного удара. Этот момент может свидетельствовать о широкой применимости модели из обобщения [Riznichenko, 1985].
Однако для рассматриваемых теоретических моделей угловой коэффициент существенно отличается от моделей, полученных на основе экспериментальных данных. Причиной этого может быть отсутствие статистики для крупных землетрясений в моделях 4–6 из табл. 1. На рис. 4, б, вместе с регрессиями из табл. 1 показаны средние значения логарифма радиуса (lgr)AV, в зависимости от MW на разных интервалах магнитуд (серая линия) и линейная регрессия построенной зависимости (lgr)AV (малиновая линия). Усреднение проводилось с учетом числа моделей, применимых при рассматриваемых значениях магнитуд, в диапазоне MW=3.5–7.2, который представляет интерес для последующего применения к анализу динамических параметров землетрясений на территории Алтае-Саянской горной области. Усредненная зависимость (lgr)AV от магнитуды MW получилась в форме ломаной линии из-за изменений числа моделей в точках, где начинается или заканчивается та или иная регрессия.
По усредненным значениям lgr получено уравнение линейной регрессии:
lg(rB[м])=0.45MW+0.96, (4)
где индекс «B» указывает на то, что рассматривается радиус очага по модели Брюна [Brune, 1970, 1971]. Коэффициент детерминации R2, определяющий соответствие модели (4) и усредненной зависимости (lgr)AV (серая линия на рис. 4, б), равен 0.67. Согласно [Aivazian, Mkhitarian, 2001], такую модель можно считать приемлемой, так как R2>0.5. Коэффициент корреляции Пирсона между зависимостями, показанными серой и малиновой линиями на рис. 4, б, составляет ρ=0.84. В случае линейной регрессии значение ρ=(R2)1/2 [Aivazian, Mkhitarian, 2001; Aivazian, 2001].
Полученная модельная регрессия наиболее приближена к модели из работы [Bormann et al., 2009].
Для вывода удобного выражения, позволяющего получить оценочный расчет сброшенных напряжений по известным значениям магнитуды MW или сейсмического момента M0, прологарифмируем (1) и подставим в полученное выражение вместо lgr линейную регрессию (4). В результате получим:
lg(∆σ[МПа])=lg(7/16)+lg(M0[Н⋅м])–1.35MW–8.88. (5)
Если выразить в (5) моментную магнитуду через сейсмический момент по формуле Канамори [Kanamori, 1977]
MW=2/3(lg(M0[Н⋅м])–9.1), (6)
можно легко прийти к окончательному выражению:
lg(∆σ[МПа])=0.1·lg(M0[Н⋅м])–1.05. (7)
Выражение, связывающее сброшенные напряжения с моментными магнитудами, которое эквивалентно (7), можно записать в форме:
lg(∆σ[МПа])=0.15MW–0.14. (8)
Для приведенной сейсмической энергии, значения которой пропорциональны ∆σ, также справедливы регрессионные зависимости, аналогичные (7), (8). После подстановки в (3) значений модуля сдвига G≅2⋅103 МПа и коэффициента k для модели Брюна k=0.37, логарифмирования (3) и замены lg (∆σ) согласно (7), (8) можно получить следующие выражения:
lgePR=0.1⋅lg(M0[Н⋅м])–4.97, lgePR=0.15MW–4.06. (9)
Таблица 1. Модельные зависимости радиуса очага, выраженного в метрах, от моментной магнитуды, количество и диапазон магнитуд исследованных событий и источник
Table 1. Model relationships between the source radius (m) and the moment magnitude; the number and range of magnitudes of the studied events; the source
№ | lg(r, [м]) | Количество | Диапазон значений магнитуды МW | Источник |
Теоретические | ||||
1 | 0.5MW+0.85 | Не применимо | 4.5–9.0 | [Bormann et al., 2009] |
2 | 0.5MW+0.58 | –/– | 3.0–8.0 | [Boore, 2003] |
3 | 0.4MW+1.50 | –/– | 0.12–9.20 | [Riznichenko, 1985] |
Экспериментальные | ||||
4 | 0.2MW+1.80 | 183 | 2.5–5.5 | [Sycheva, Bogomolov, 2020] |
5 | 0.1MW+2.60 | 63 | 1.7–6.1 | [Dobrynina, 2009] |
6 | 0.22MW+2.02 | 90 | 1.6–4.2 | [Kim et al., 1989] |
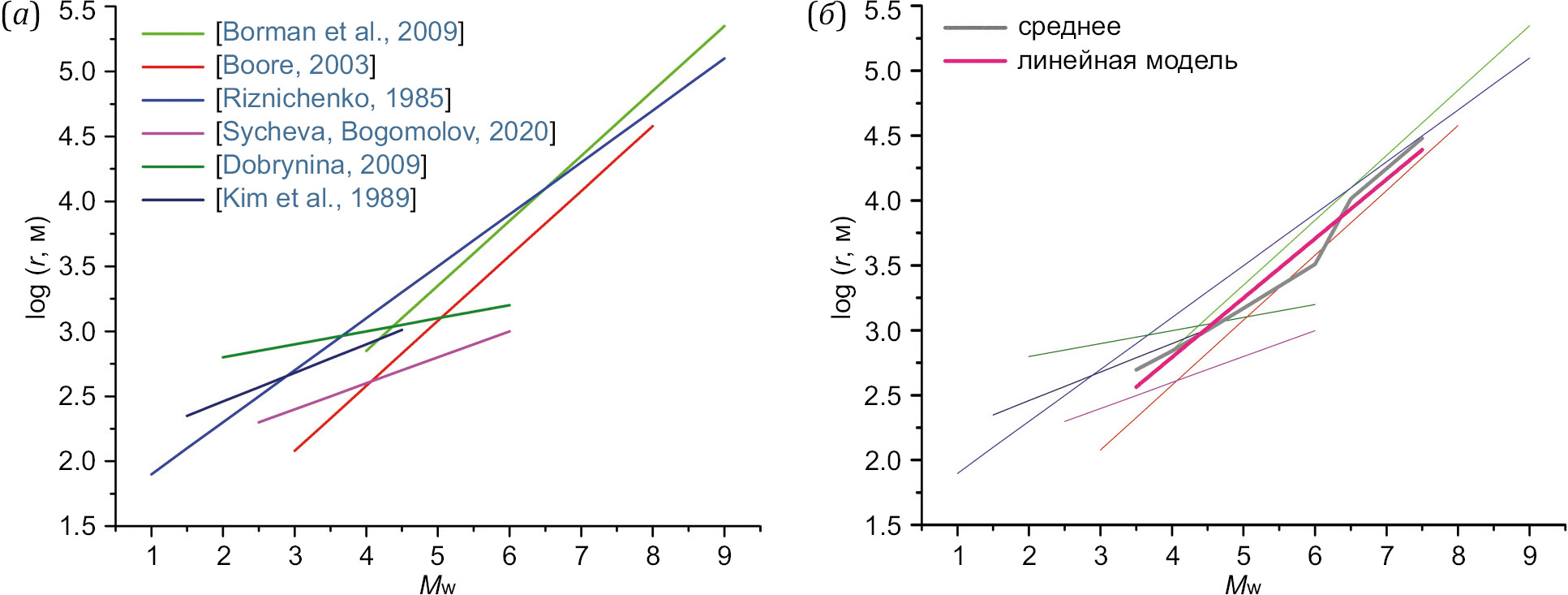
Рис. 4. Зависимость радиуса очага rB от моментной магнитуды MW для рассматриваемых моделей (а) (табл. 1) и среднее значение по моделям и ее регрессия (б).
Fig. 4. Dependence of the source radius rB on the moment magnitude MW for the models under consideration (а) (Table 1), and the average value for the models and its regression (б).
РЕЗУЛЬТАТЫ
Подход, описанный в методике, был использован для расчета радиуса очага, сброшенных напряжений и приведенной сейсмической энергии для 69 рассматриваемых землетрясений. В Прил. 1, табл. 1.1, представлены результаты расчетов r и ∆σ для модели Брюна. Также приведены относительные значения радиусов и сброшенных напряжений, в качестве нормировочного выбрано Чуйское землетрясение 27.09.2003 г., МW=7.2. Для очага этого землетрясения радиус по модели Брюна r=~15800 м, величина сброшенных напряжений ∆σ=~10 МПа.
Прил. 1, табл. 1.1, также содержит значение приведенной сейсмической энергии, которая, как уже отмечалось выше, не зависит от выбора модели очага. Для землетрясений с магнитудой (допустим, M=4–5) характерный порядок величины ePR~10–3, что находится в соответствии с результатами [Dobrynina, 2009; Kocharyan, 2012]. Для рассматриваемого класса землетрясений (MW=3.7–7.2) среднее значение радиуса очага составляет 2932 м, медианное – 1995 м, среднее значение сброса напряжений соответствует 4.72 МПа, медианное – 4.23 МПа, среднее значение приведенной сейсмической энергии ePR=0.57⋅10–3, медианное значение ePR=0.51⋅10–3. Незначительная разница между средним и медианным значением рассматриваемых параметров обусловлена тем, что для 80 % землетрясений магнитуда варьируется в диапазоне 4.2–5.7, что обеспечивает незначительные отклонения в рассчитываемых параметрах.
На рис. 5 представлено распределение логарифма интенсивности СТД [Lukk, Yunga, 1979], полученной в работе [Sycheva, 2023] для Алтае-Саянской горной области и показано положение исследуемых землетрясений (69 событий). Значительная часть рассматриваемых событий попала в области, где значение интенсивности СТД превышает 10–10 год–1, а значительный сброс напряжений произошел в областях, где интенсивность СТД превышает 10–9 год–1 (очаговая область Чуйского землетрясения 2003 г., Хубсугульского землетрясения 2021 г., тувинских землетрясений 2011, 2012 гг.).
Для верификации оценок сброшенных напряжений и приведенной сейсмической энергии, сделанных с помощью регрессий (7) – (9), т.е. по-существу феноменологическим методом, можно использовать результаты работ [Zakharova et al., 2009; Chepkunas, Malyanova, 2017, 2018], где по очаговым спектрам определены динамические параметры для ряда сильных землетрясений мира, в том числе для пяти землетрясений в Алтае-Саянском регионе. Данные по динамическим параметрам, полученные обоими методами, имеются для таких землетрясений, как (рис. 6):
– Чуйское землетрясение 27.09.2003 г., MW=7.2 (№ 20 в Прил. 1, табл. 1.1);
– афтершок Чуйского землетрясения 27.09.2003 г., MW=6.4 (№ 21);
– афтершок 01.10.2003 г., MW=6.6 (№ 22);
– I Тувинское землетрясение 29.12.2011 г., MW=6.7 (№ 41);
– II Тувинское землетрясение 26.02.2012 г., MW=6.6 (№ 42).
Для этих пяти землетрясений в табл. 2 представлены значения некоторых динамических параметров, определенных двумя методами. В цитированных работах авторов из Единой геофизической службы РАН динамические параметры рассчитаны по спектрам продольных волн, зарегистрированных цифровой аппаратурой STS-1 на телесейсмических расстояниях ∆≤100° по записям одной станции – «Обнинск» (OBN, 55.1146° с.ш. и 36.5674° в.д., h=160 м). Интервал эпицентральных расстояний для рассматриваемых землетрясений меняется в диапазоне ∆=30.9–34.7°. Согласно работам [Zakharova et al., 2009; Chepkunas, Malyanova, 2017, 2018], станционные спектры перечисленных землетрясений (табл. 2) были приведены к очагу перед определением спектральных параметров Ω0 и f0.
При анализе табл. 2 обращает на себя внимание расхождение значений скалярного сейсмического момента и размера очага, полученных двумя разными методами. Для M0 это обусловлено тем, что, с одной стороны, в работах [Zakharova et al., 2009; Chepkunas, Malyanova, 2017, 2018] скалярный сейсмический момент определялся по параметрам спектров продольных, а не поперечных волн. А с другой стороны, различие в M0 (т.е. энергетических характеристиках) может проистекать из-за погрешности в глубине гипоцентров по каталогу СМТ для рассматриваемых землетрясений. В работах, где использовались параметры спектров, наибольший размер очага (его длина) определялся по модели Хаскелла, а не по модели Брюна (обзор моделей в работе [Aptekman et al., 1989]), так что различие значений L и r в табл. 2 неудивительно. Динамические параметры M0, r, L являются промежуточными при оценочных расчетах сброшенных напряжений. С учетом изложенного при сравнении значений ∆σ, полученных двумя методами, ставится вопрос о наличии или отсутствии соответствия, по крайней мере, по порядку величины.
Согласно табл. 2 в четырех случаях из пяти расчет по очаговому спектру дал более высокие значения сброшенных напряжений, чем на основе регрессий. При этом отношение ∆σспектр/∆σрегрессия в трех случаях не превышает 1.6, а в одном случае (афтершок Чуйского землетрясения 01.10.2003 г.) достигает 2.4. Для Чуйского землетрясения 27.09.2003 г. соотношение между значениями ∆σ обратное: ∆σспектр~0.55∆σрегрессия. Магнитуды рассматриваемых пяти землетрясений лежат в узком диапазоне, и для них обретает смысл среднее арифметическое значение ∆σ. Для двух методов расчета сброшенных напряжений средние значения, которые приведены в табл. 2, отличаются примерно на 20 %. Такое же различие между средневзвешенными значениями ∆σ по двум методам. Для расчета по спектрам среднеарифметическое значение ∆σ оказалось больше, а средневзвешенное – меньше, чем для метода с использованием регрессии.
Таким образом, различие значений сброшенных напряжений по двум методам меньше на порядок (максимум в 2.4 раза), что свидетельствует о возможности использования полученных данных (Прил. 1, табл. 1.1) для ∆σ и пропорциональной ему ePR в Алтае-Саянском регионе. Вместе с тем для афтершоков Чуйского землетрясения, у которых магнитуды меньше, но сброшенные напряжения больше, чем для очага главного события, параметры не согласуются с регрессией. Этот пример показывает, что в случае афтершоков предложенный феноменологический подход может приводить к ошибкам.
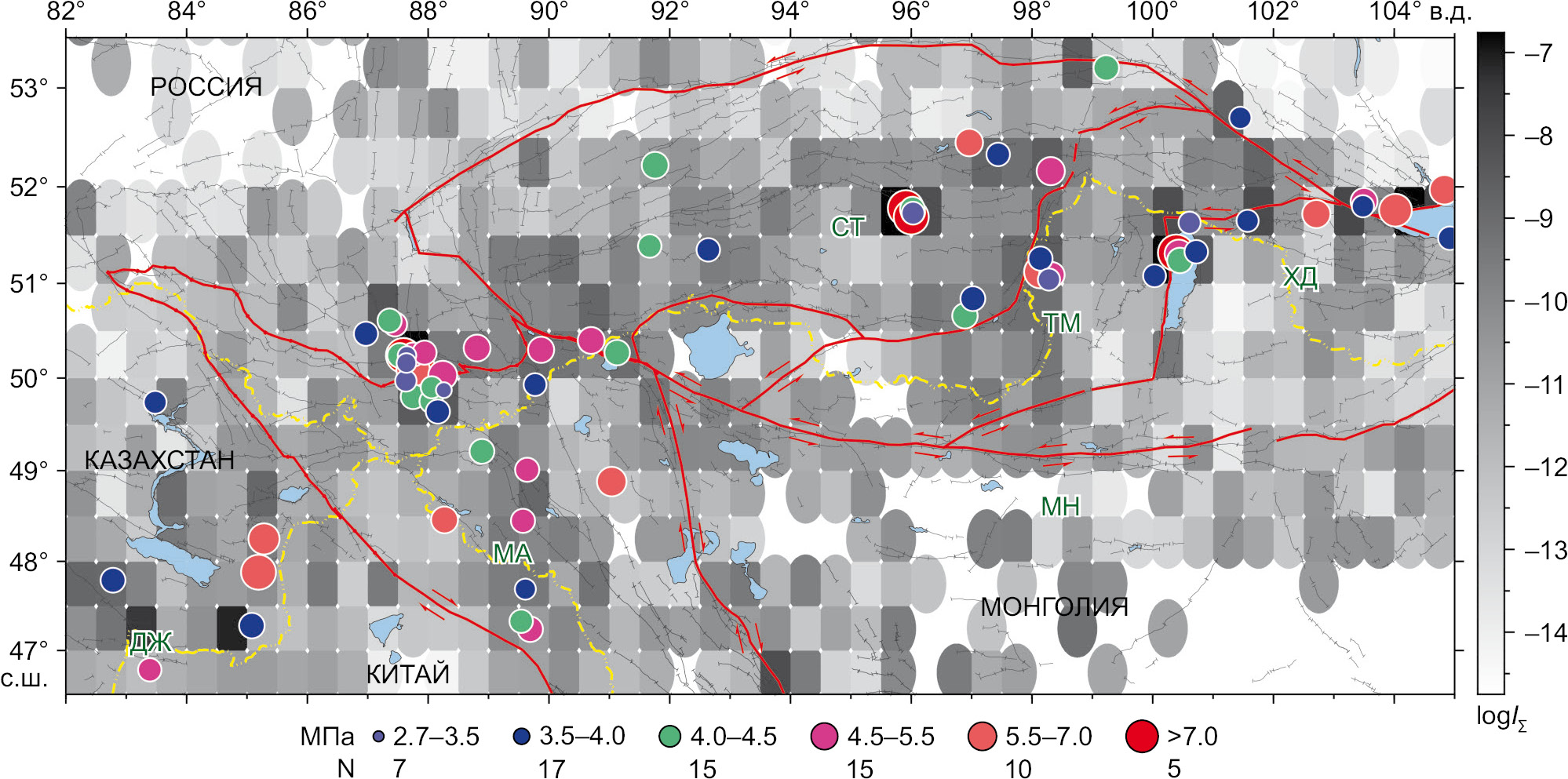
Рис. 5. Эпицентральное положение исследуемых землетрясений.
Цвет кружка зависит от величины сброшенных напряжений (см. легенду внизу карты). Сброшенные напряжения рассчитаны по модели очага землетрясения Брюна [Brune, 1970, 1971]. Названия блоков см. рис. 1.
Fig. 5. Epicentral location of the earthquakes studied.
The color of the circle fill depends on the magnitude of the released stresses (see the map legend). The released stresses are calculated using the Brune earthquake source model [Brune, 1970, 1971]. For block names, see Fig. 1.
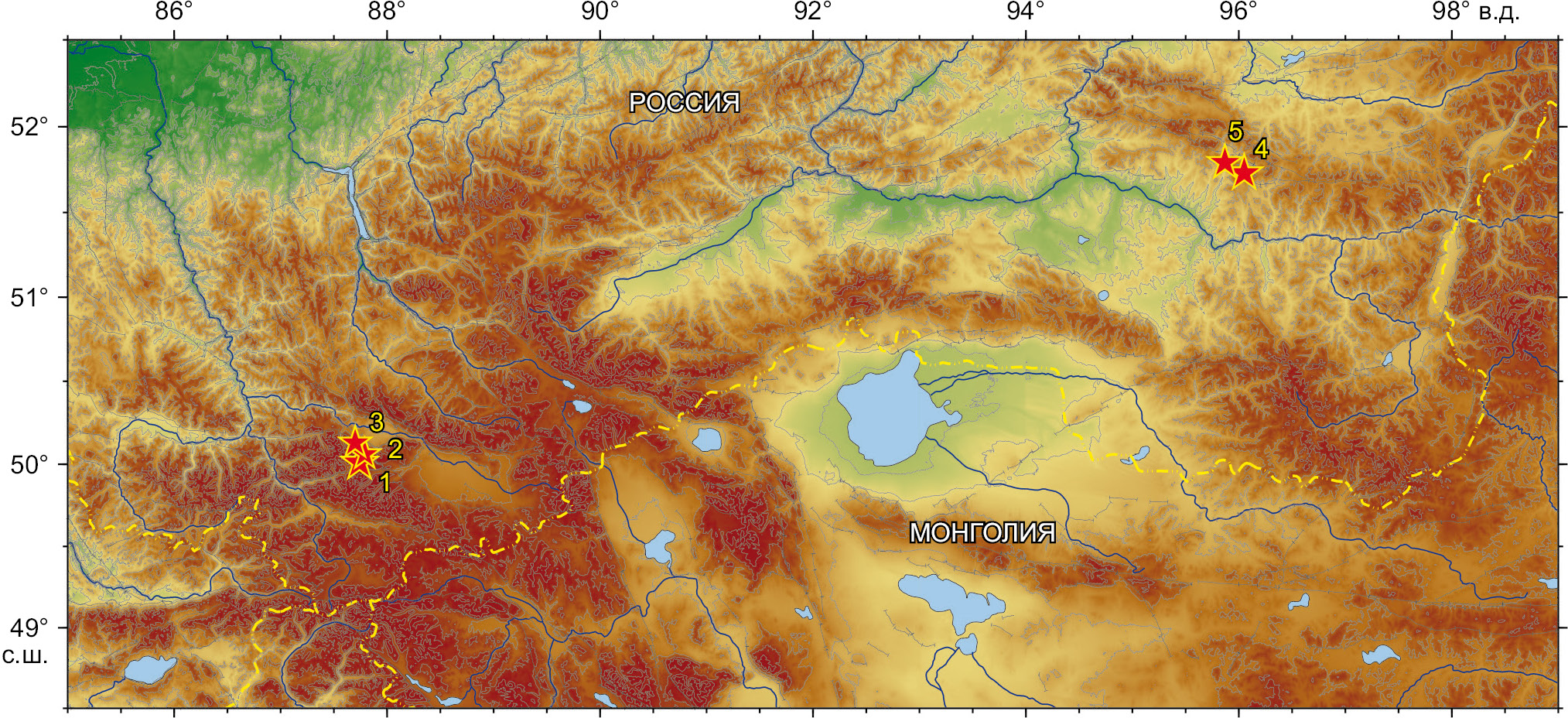
Рис. 6. Эпицентральное положение тестовых землетрясений (5 событий). Номер землетрясения соответствует номеру в табл. 2.
Fig. 6. Epicentral location of test earthquakes (5 events). The earthquake number corresponds to the number in Table 2.
Таблица 2. Значения скалярного сейсмического момента, длины разрыва L, радиуса очага и сброса касательных напряжений (согласно материалам [Zakharova et al., 2009; Chepkunas, Malyanova, 2017, 2018] и результатам данной работы (Прил. 1, табл. 1.1))
Table 2. The values of scalar seismic moment, rupture length L, source radius and shear stress drop, according to [Zakharova et al., 2009; Chepkunas, Malyanova, 2017, 2018] and the results presented here (App. 1, Table 1.1)
№ | Дата | Время | По очаговому спектру | Феноменологический подход | ||||||||||
MW | M0·1019, Н·м | L·103, м | ∆σ·105, Н/м2 | MW | M0·1019, Н·м | rB·103, м | ∆σ·105, Н/м2 | |||||||
1 | 27.09.2003 | 11:33:26.5 | 6.9 | 2.2 | 24 | 56 | 7.2 | 9.38 | 15.8 | 103.1 | ||||
2 | 27.09.2003 | 18:52:47.1 | 6.2 | 0.2 | 9 | 96 | 6.4 | 0.45 | 6.92 | 60 | ||||
3 | 01.10.2003 | 01:03:25.0 | 6.3 | 0.4 | 9 | 192 | 6.6 | 1.13 | 8.51 | 80 | ||||
4 | 27.12.2011 | 15:21:54.9 | 6.6 | 0.9 | 14 | 115 | 6.7 | 1.38 | 9.44 | 72 | ||||
5 | 26.02.2012 | 06:17:18.0 | 6.8 | 1.5 | 18 | 90 | 6.6 | 1.2 | 8.5 | 84 | ||||
Среднее значение ∆σ·105 | 110 | Среднее значение ∆σ·105 | 80 | |||||||||||
Средневзвешенное ∆σ·105 | 76.5 | Средневзвешенное ∆σ·105 | 92.6 | |||||||||||
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Значения сброшенных напряжений относятся к области очага, т.е. к весьма малому объему среды. Для анализа взаимосвязи сброшенных напряжений с геодинамической обстановкой и параметрами напряженно-деформированного состояния земной коры (которые усреднены на больших масштабах) необходимо провести усреднение ∆σ по некоторой выборке событий. Для формирования выборок внутри изучаемого региона выделялись зоны размером 1×1°. Для разных событий объемы очагов, в которых происходит снятие касательных напряжений, различны, и составляют разную долю от объема среды для рассматриваемой зоны, поэтому при усреднении сброшенных напряжений по выборке естественно вводить весовой множитель gi, пропорциональный объему очага: т.е. gi~ri3, где i – номер события в выборке. При этом средневзвешенное значение сброшенных напряжений <Δσ>AW будет определяться выражением:
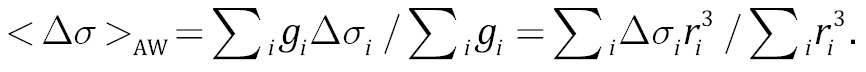 (10)
(10)
Поскольку в (10) произведение Δσiri3=7/16(M0)i, это выражение можно свести к следующей расчетной формуле для средневзвешенного значения сброшенных напряжений:
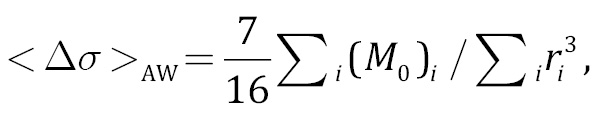 (11)
(11)
где суммирование идет по всем событиям в выборке, M0i, – скалярный сейсмический момент землетрясения номер «i», ri – значение радиуса очага, вычисленное по модели Брюна.
При усреднении значения ∆σAW получены для 36 ячеек размером 1×1°. В 24 ячейки попало по одному событию, и усредненное значение ∆σAW соответствует сбросу напряжения при самом землетрясении. Для остальных ячеек усредненное значение ∆σAW зависит от количества землетрясений в ячейке.
На рис 7, а, показаны ячейки (отображены в виде эллипсов), для которых получены значения ∆σAW. Для визуализации результатов расчета (построения карты) используется программа nearneighbor пакета GMT (Generic Mapping Tools, https://www.generic-mapping-tools.org/), в которой реализован алгоритм ближайшего соседа для присвоения среднего значения каждому узлу, который имеет одну или несколько точек в пределах заданного радиуса от узла. В этом программном пакете узел считается центром эллиптической (круговой) зоны, на которую распространяется вычисленное среднее значение. Цвет ячейки зависит от величины логарифма усредненных сброшенных напряжений (логарифмический масштаб позволяет более контрастно выделить ячейки с минимальным значением сброшенных напряжений). В каждой ячейке показано количество событий, попавших в нее. Максимальное количество событий попало в ячейку, которая совпадает с очаговой областью Чуйского землетрясения. Для ячеек темно-голубого цвета (15 ячеек из 36) ∆σAW≤4 МПа и для семи зон ∆σAW≥6.5 МПа (очаговая область Чуйского землетрясения ~9 МПа, тувинских землетрясений ~8 МПа, Бусийнгольского ~6.5 МПа и др.).
Значительный уровень сброшенных напряжений приходится на северные границы Монголо-Алтайского блока (район Чуйского землетрясения, 27.09.2003 г., MW=7.2, и восточнее), северо-западные и юго-восточные границы Тувино-Монгольского блока, юго-восточную часть Саяно-Тувинского блока, на Джунгарском блоке также выделяется территория, для которой характерен значительный уровень сброса напряжений (рис. 7, а).
На рис. 7, б, представлено распределение логарифма суммарной приведенной сейсмической энергии, рассчитанной так же для ячеек размером 1×1°. Для ячеек, куда попало только одно событие, отображено само значение lgePR. Естественно, что площадное распределение lg(ΣePR) сходно с распределением lg∆σAW (рис. 7, а) в силу соотношения (4). Некоторые отличия (например, см. ячейки южнее северной границы Монголо-Алтайского блока) обусловлены тем, что суммирование ePR внутри ячейки проводится независимо от объема очагов. По рис. 7, б, можно выделить зоны с максимальными значениями суммарной ePR: северная граница Монголо-Алтайского блока, ΣePR~(0.8–6.0)⋅10–3, а также северо-западная и юго-восточная граница Тувино-Монгольского блока, ΣePR~(0.2–3.0)⋅10–3.
В результате применения феноменологического подхода к расчету радиуса очага (без построения очагового спектра сейсмограмм землетрясения) оценены значения сброшенных касательных напряжений и приведенной сейсмической энергии для 69 землетрясений, произошедших на территории Алтае-Саянской горной области. Это позволило сопоставлять значения ∆σ и ePR для разных событий и разных зон (в Прил. 1, табл. 1.1 для удобства приведены относительные значения ∆σ).
Для сравнения величины сброшенных напряжений (динамический параметр) с распределением коэффициента Лоде – Надаи (кинематический параметр) на исследуемой территории построена совместная карта рассматриваемых характеристик (рис. 8). Сравнение указанных параметров проведено в пределах территории, для которой получено распределение коэффициента Лоде – Надаи [Sycheva, Rebetsky, 2024]. Из рассматриваемых событий в ячейки с известным значением коэффициента Лоде – Надаи попало 59 землетрясений. Посчитано количество событий и суммарный сброс напряжений для землетрясений в областях с разным режимом деформации, который определяется величиной коэффициента Лоде – Надаи. В табл. 3 представлены некоторые результаты количественного анализа. В областях одноосного растяжения (µε≤–0.6, по легенде оттенки синего цвета) рассматриваемые события отсутствуют.
По данным табл. 2, двадцать шесть (~44 %) землетрясений локализованы в области с деформацией одноосного сжатия и преобладания одноосного сжатия. Суммарный сброс напряжений, усредненный с весовым множителем, пропорциональным объему очага ∆σAW, рассчитанному по выражению (11), составил 4 МПа. В области с деформацией чистого сдвига локализовано 27 (~46 %) землетрясений и сброс напряжений ∆σAW составил 8.9 МПа. В области с деформацией преобладания одноосного растяжения произошло 6 (10 %) землетрясений и сброс напряжений ∆σAW составил 5.6 МПа. Сравнительный анализ кинематических и динамических параметров землетрясений показал, что значительная часть сброса напряжений произошла в областях с µε>0.2, что соответствует режиму деформации одноосного сжатия и преобладания одноосного сжатия. Очаговая область Чуйского землетрясения расположена в области с режимом деформации преобладания одноосного сжатия (рис. 8). Сброс напряжений при Чуйском землетрясении составил ~10 МПа.
Завершая описание распределений приведенной сейсмической энергии и сброшенных напряжений для землетрясений в Алтае-Саянском регионе, подчеркнем особенности предложенного феноменологического метода. Метод опирается на обобщения, касающиеся взаимосвязи между радиусом очага и скалярным сейсмическим моментом (или моментной магнитудой). Феноменологическая модель (регрессия) содержит большой объем данных из разных работ. Это позволяет обойтись без определения значений угловой частоты, которые во многих случаях получаются с большим разбросом. Тем не менее применимость феноменологического метода для других сейсмоактивных регионов остается вопросом, который должен рассматриваться в каждом конкретном случае (важно, в частности, насколько мала доля афтершоков в выборке событий с известным сейсмическим моментом). Предложенный метод оценки сброшенных напряжений и приведенной сейсмической энергии позволит расширить имеющиеся банки данных по динамическим параметрам дополнительной информацией.
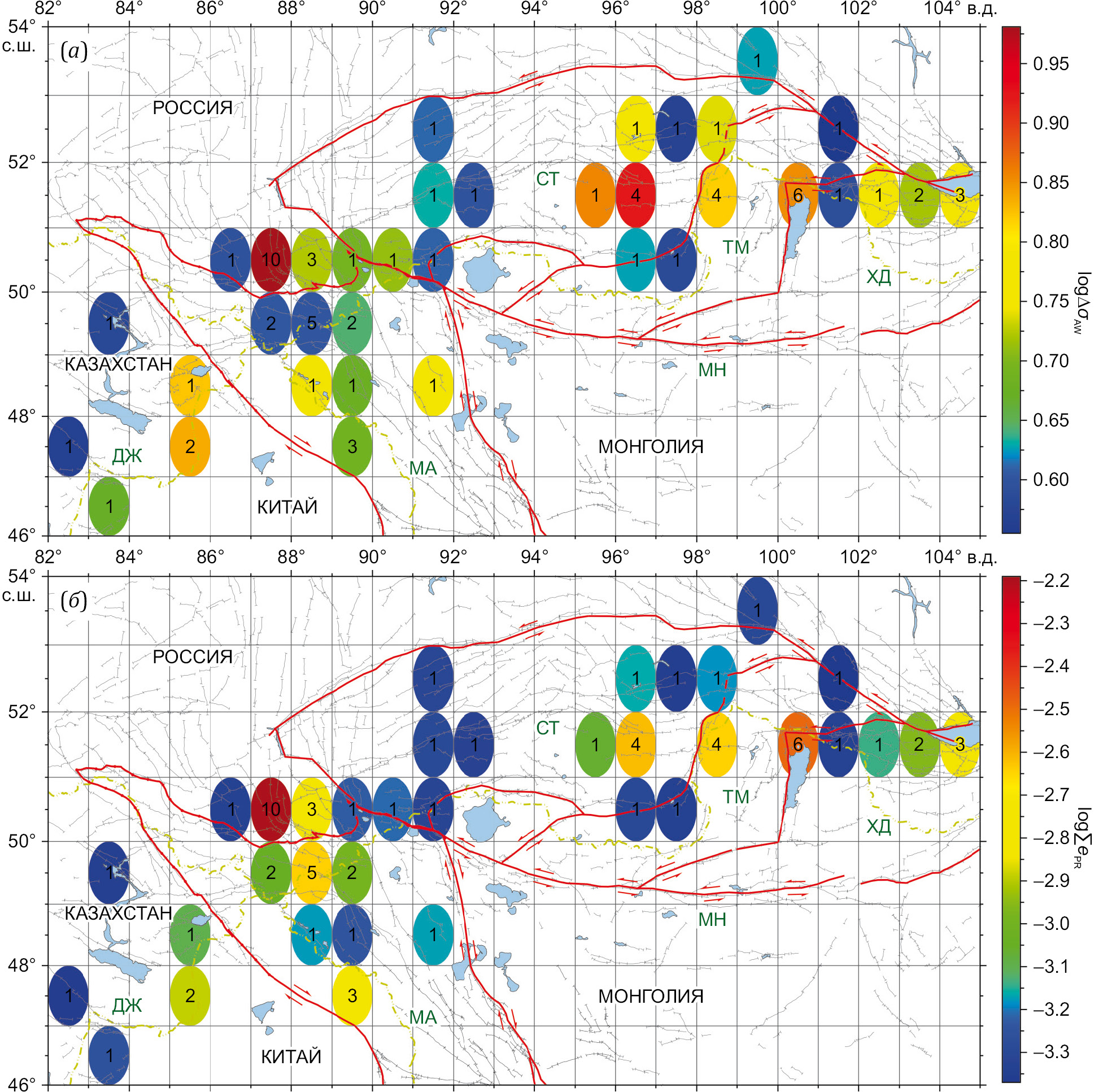
Рис. 7. Распределение значений логарифма: (а) – сброшенных напряжений ∆σAW; (б) – суммарной приведенной сейсмической энергии. Количество событий, попавших в ячейку, отмечено цифрами. Названия блоков см. рис. 1.
Fig. 7. Distribution of logarithm values: (a) – dropped stresses ∆σAW; (б) – total reduced seismic energy. The numbers indicate the number of events fell therein. For block names, see Fig. 1.
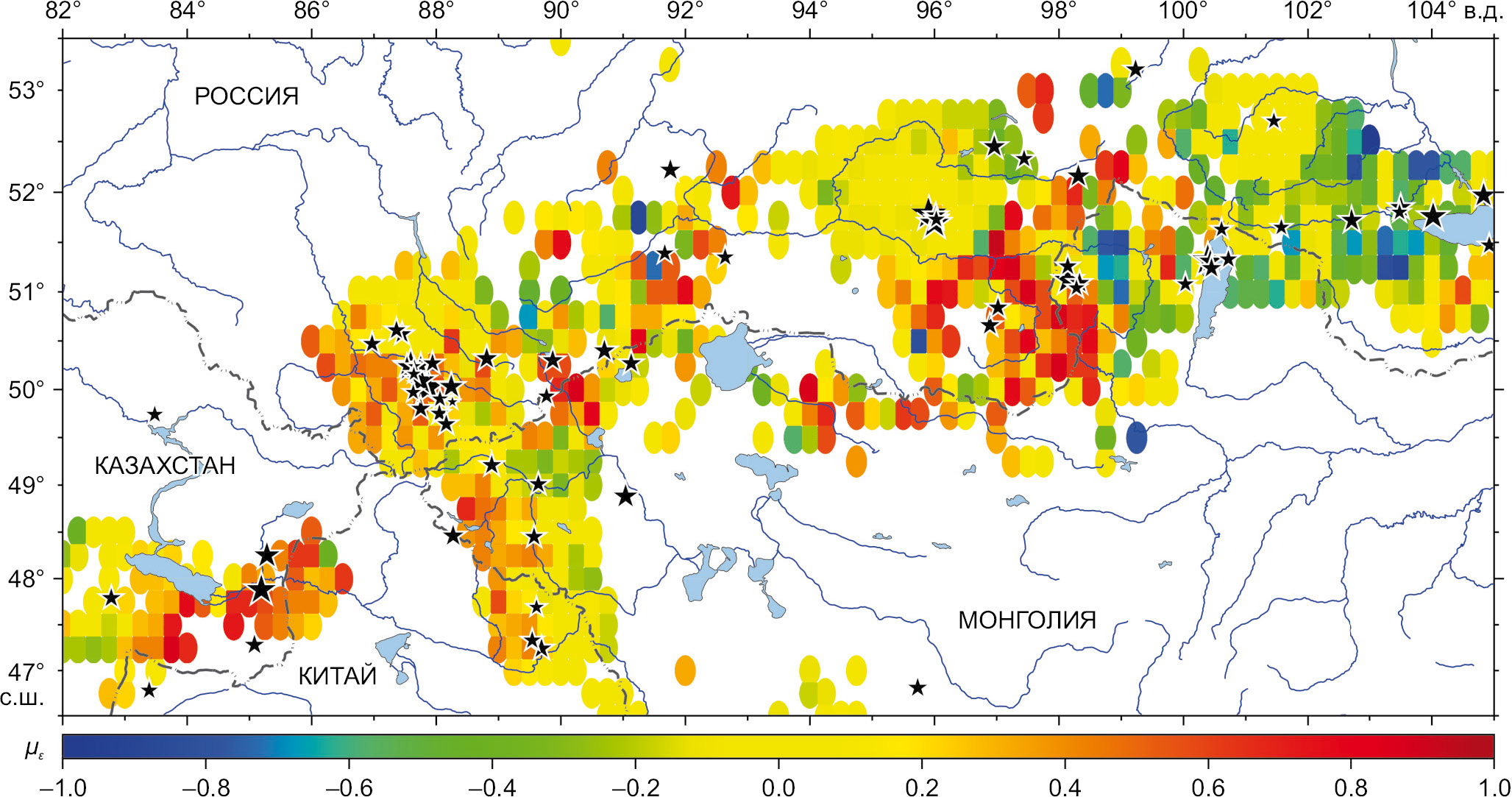
Рис. 8. Эпицентральное положение землетрясений на фоне распределения коэффициента Лоде – Надаи по материалам [Sycheva, Rebetsky, 2024].
Fig. 8. Epicentral location of earthquakes on the background distribution of the Lode – Nadai coefficient, after [Sycheva, Rebetsky, 2024].
Таблица 3. Значения сброшенных напряжений ∆σ и коэффициента Лоде – Надаи µε [Sycheva, Rebetsky, 2024] в зонах с различными режимами деформации
Table 3. The stress drop values ∆σ and the Lode – Nadai coefficient µε [Sycheva, Rebetsky, 2024] in zones of different defotmation modes
Показатель | Режим деформации | |||||||||||||
Одноосное сжатие | Преобладание одноосного сжатия | Чистый сдвиг | Преобладание одноосного растяжения | Одноосное растяжение | ||||||||||
με | 0.6≤με≤1.0 | 0.2<με<0.6 | –0.2≤με≤0.2 | –0.6<με<–0.2 | –1.0≤με≤–0.6 | |||||||||
∆σAW, МПа | 4.0 | 8.9 | 7.3 | 5.6 | 0 | |||||||||
N | 2 | 24 | 27 | 6 | 0 | |||||||||
ЗАКЛЮЧЕНИЕ
В работе предложен феноменологический подход к расчету радиуса очага землетрясения, не требующий построения очагового спектра. Проанализированы ранее установленные теоретические и эмпирические соотношения между радиусом очага и моментной магнитудой. На основе усреднения этих соотношений выведены выражения для расчета сброса касательных напряжений и приведенной сейсмической энергии по данным о скалярном сейсмическом моменте, или моментной магнитуде. Предложенный подход применен для землетрясений Алтае-Саянской горной области с целью увеличения объема данных по сброшенным напряжениям ∆σ и приведенной сейсмической энергии ePR. Имеется соответствие оценок сброшенных напряжений для пяти тестовых землетрясений, сделанных на основе регрессий (феноменологический подход) и полученных ранее при расчетах по параметрам очаговых спектров.
Среди землетрясений, произошедших на этой территории в 1978–2025 г., выделено 69 событий, для которых в каталоге СМТ приведены значения скалярного сейсмического момента и моментной магнитуды (MW=4.75–5.5). Для этих событий проведены оценки ∆σ и ePR и сформирован банк данных по динамическим параметрам в виде Прил. 1, табл. 1.1. Для картирования площадных распределений сброшенных напряжений предложено использовать средневзвешенные значения ∆σ, в которых учтено различие объемов очагов усредняемых (компактно расположенных) событий. Для большинства зон 1×1°, в которых проводилось усреднение сброшенных напряжений, значения ∆σAW не превышают 4.5 МПА, а максимальное значение средневзвешенного сброса напряжений ∆σAW~9 МПа. Для этих же зон на изучаемой территории характерные значения приведенной сейсмической энергии составляют ePR~0.58⋅10–3.
Сравнительный анализ кинематических и динамических параметров землетрясений показал, что значительная часть сброса напряжений ∆σAW произошла в областях с µε>0.2, что соответствует режиму деформации одноосного сжатия и преобладания одноосного сжатия.
ПРИЛОЖЕНИЕ 1 / APPENDIX 1
Таблица 1.1. Динамические параметры землетрясений (69 событий) Алтае-Саянской горной области
Table 1.1. Dynamic parameters of earthquakes (69 events) in the Altai-Sayan mountain region
№ | Дата | Время | φ, ° | λ, ° | H, км | MW | M0·1017 (Н·м) | rB, м | ∆σ, МПа | ePR·10–3 | rB норм | ∆σ норм |
1 | 03.08.1978 | 06:07:41.10 | 52.45 | 96.96 | 10.0 | 5.6 | 3.60 | 3020 | 5.72 | 0.69 | 0.19 | 0.56 |
2 | 16.08.1981 | 17:54:18.10 | 50.84 | 97.02 | 15.0 | 5.2 | 0.70 | 1995 | 3.86 | 0.46 | 0.13 | 0.37 |
3 | 03.08.1982 | 04:50:29.60 | 49.01 | 89.64 | 10.0 | 5.1 | 0.62 | 1799 | 4.67 | 0.56 | 0.11 | 0.45 |
4 | 24.04.1986 | 00:22:17.20 | 47.33 | 89.54 | 33.0 | 5.0 | 0.43 | 1622 | 4.44 | 0.53 | 0.10 | 0.43 |
5 | 04.11.1986 | 16:19:20.20 | 50.32 | 88.81 | 15.0 | 5.5 | 2.44 | 2723 | 5.29 | 0.63 | 0.17 | 0.51 |
6 | 18.09.1987 | 21:58:39.90 | 47.24 | 89.69 | 15.0 | 5.3 | 1.28 | 2213 | 5.17 | 0.62 | 0.14 | 0.50 |
7 | 30.06.1988 | 15:25:13.90 | 50.27 | 91.13 | 15.0 | 5.3 | 1.01 | 2213 | 4.08 | 0.49 | 0.14 | 0.40 |
8 | 23.07.1988 | 07:38:15.00 | 48.88 | 91.04 | 18.0 | 5.9 | 8.99 | 4121 | 5.62 | 0.67 | 0.26 | 0.55 |
9 | 14.06.1990 | 12:47:32.60 | 47.88 | 85.19 | 36.0 | 6.6 | 97.30 | 8511 | 6.90 | 0.83 | 0.54 | 0.67 |
10 | 03.08.1990 | 09:15:12.50 | 48.25 | 85.28 | 32.0 | 6.1 | 19.80 | 5070 | 6.65 | 0.80 | 0.32 | 0.65 |
11 | 27.12.1991 | 09:09:45.80 | 51.12 | 98.14 | 15.0 | 6.3 | 37.50 | 6237 | 6.76 | 0.81 | 0.39 | 0.66 |
12 | 22.06.1995 | 01:01:23.80 | 50.30 | 89.87 | 15.0 | 5.4 | 1.67 | 2455 | 4.94 | 0.59 | 0.15 | 0.48 |
13 | 29.06.1995 | 23:02:33.10 | 51.72 | 102.71 | 15.0 | 5.7 | 5.20 | 3350 | 6.05 | 0.73 | 0.21 | 0.59 |
14 | 12.03.1996 | 18:43:48.30 | 48.46 | 88.27 | 17.0 | 5.5 | 2.56 | 2723 | 5.55 | 0.67 | 0.17 | 0.54 |
15 | 12.07.1998 | 07:16:21.20 | 47.79 | 82.78 | 35.4 | 5.2 | 0.67 | 1995 | 3.68 | 0.44 | 0.13 | 0.36 |
16 | 21.11.1998 | 16:59:54.10 | 49.21 | 88.89 | 15.0 | 5.2 | 0.74 | 1995 | 4.08 | 0.49 | 0.13 | 0.40 |
17 | 25.02.1999 | 18:58:39.00 | 51.97 | 104.83 | 21.0 | 5.9 | 8.91 | 4121 | 5.57 | 0.67 | 0.26 | 0.54 |
18 | 31.05.2000 | 16:28:07.80 | 51.47 | 104.92 | 15.0 | 5.0 | 0.38 | 1622 | 3.91 | 0.47 | 0.10 | 0.38 |
19 | 07.05.2003 | 02:58:02.01 | 48.45 | 89.57 | 33.0 | 5.1 | 0.64 | 1799 | 4.78 | 0.57 | 0.11 | 0.46 |
20 | 27.09.2003 | 11:33:36.25 | 50.02 | 87.86 | 15.0 | 7.2 | 938.00 | 15849 | 10.31 | 1.24 | 1.00 | 1.00 |
21 | 27.09.2003 | 18:52:52.93 | 50.09 | 87.75 | 15.0 | 6.4 | 45.20 | 6918 | 5.97 | 0.72 | 0.44 | 0.58 |
22 | 01.10.2003 | 01:03:29.98 | 50.24 | 87.59 | 15.0 | 6.6 | 113.00 | 8511 | 8.02 | 0.96 | 0.54 | 0.78 |
23 | 04.10.2003 | 14:23:29.00 | 49.87 | 88.26 | 0 | 3.7 | 0.00 | 422 | 2.61 | 0.31 | 0.03 | 0.25 |
24 | 05.10.2003 | 16:21:13.00 | 50.16 | 87.64 | 0 | 4.4 | 0.05 | 871 | 3.32 | 0.40 | 0.05 | 0.32 |
25 | 06.10.2003 | 18:30:17.40 | 50.24 | 87.65 | 0 | 4.2 | 0.03 | 708 | 3.10 | 0.37 | 0.04 | 0.30 |
26 | 09.10.2003 | 16:06:03.16 | 49.75 | 88.05 | 15.0 | 5.0 | 0.41 | 1622 | 4.24 | 0.51 | 0.10 | 0.41 |
27 | 13.10.2003 | 05:26:42.32 | 50.25 | 87.75 | 15.0 | 5.1 | 0.60 | 1799 | 4.51 | 0.54 | 0.11 | 0.44 |
28 | 17.10.2003 | 05:30:25.90 | 50.27 | 87.94 | 15.0 | 5.1 | 0.61 | 1799 | 4.55 | 0.55 | 0.11 | 0.44 |
29 | 23.10.2003 | 00:25:48.46 | 49.64 | 88.16 | 15.0 | 5.1 | 0.48 | 1799 | 3.64 | 0.44 | 0.11 | 0.35 |
30 | 11.11.2003 | 22:42:35.69 | 50.47 | 86.97 | 15.0 | 5.1 | 0.53 | 1799 | 3.95 | 0.47 | 0.11 | 0.38 |
31 | 17.11.2003 | 01:35:52.31 | 50.24 | 87.53 | 15.0 | 5.2 | 0.75 | 1995 | 4.15 | 0.50 | 0.13 | 0.40 |
32 | 15.02.2005 | 12:41:45.28 | 47.69 | 89.61 | 13.2 | 4.6 | 0.10 | 1072 | 3.70 | 0.44 | 0.07 | 0.36 |
33 | 27.04.2005 | 07:36:15.28 | 51.09 | 98.33 | 12.0 | 5.3 | 1.28 | 2213 | 5.17 | 0.62 | 0.14 | 0.50 |
34 | 22.08.2005 | 08:31:25.94 | 49.97 | 87.63 | 27.4 | 4.7 | 0.13 | 1189 | 3.31 | 0.40 | 0.07 | 0.32 |
35 | 19.01.2008 | 07:32:31.71 | 51.26 | 98.14 | 12.0 | 5.1 | 0.49 | 1799 | 3.69 | 0.44 | 0.11 | 0.36 |
36 | 29.01.2008 | 20:02:30.72 | 49.74 | 83.48 | 34.8 | 4.9 | 0.27 | 1462 | 3.82 | 0.46 | 0.09 | 0.37 |
37 | 16.08.2008 | 04:01:11.67 | 52.16 | 98.31 | 28.2 | 5.7 | 4.70 | 3350 | 5.47 | 0.66 | 0.21 | 0.53 |
38 | 27.08.2008 | 01:35:38.61 | 51.76 | 104.02 | 23.5 | 6.3 | 34.10 | 6237 | 6.15 | 0.74 | 0.39 | 0.60 |
39 | 04.08.2009 | 16:20:43.23 | 50.66 | 96.89 | 30.4 | 5.3 | 1.05 | 2213 | 4.24 | 0.51 | 0.14 | 0.41 |
40 | 10.02.2011 | 05:35:17.82 | 52.22 | 91.76 | 26.3 | 5.5 | 1.89 | 2723 | 4.10 | 0.49 | 0.17 | 0.40 |
41 | 27.12.2011 | 15:22:03.84 | 51.78 | 95.91 | 19.5 | 6.7 | 138.00 | 9441 | 7.18 | 0.86 | 0.60 | 0.70 |
42 | 26.02.2012 | 06:17:24.34 | 51.69 | 96.00 | 20.5 | 6.6 | 119.00 | 8511 | 8.44 | 1.01 | 0.54 | 0.82 |
43 | 26.02.2012 | 11:59:05.84 | 51.74 | 96.03 | 17.6 | 5.1 | 0.54 | 1799 | 4.02 | 0.48 | 0.11 | 0.39 |
44 | 06.06.2012 | 14:04:17.47 | 51.77 | 96.02 | 28.0 | 5.2 | 0.78 | 1995 | 4.31 | 0.52 | 0.13 | 0.42 |
45 | 27.07.2012 | 03:58:13.43 | 51.73 | 96.03 | 17.9 | 4.9 | 0.25 | 1462 | 3.46 | 0.41 | 0.09 | 0.34 |
46 | 30.07.2012 | 22:30:43.73 | 50.61 | 87.36 | 25.9 | 5.1 | 0.57 | 1799 | 4.29 | 0.51 | 0.11 | 0.42 |
47 | 24.01.2013 | 07:35:37.30 | 49.80 | 87.75 | 19.6 | 5.2 | 0.76 | 1995 | 4.16 | 0.50 | 0.13 | 0.40 |
48 | 30.04.2013 | 01:03:33.34 | 51.35 | 92.64 | 12.0 | 5.0 | 0.39 | 1622 | 3.98 | 0.48 | 0.10 | 0.39 |
49 | 01.11.2014 | 00:52:01.56 | 52.70 | 101.45 | 29.8 | 4.8 | 0.19 | 1318 | 3.59 | 0.43 | 0.08 | 0.35 |
50 | 05.12.2014 | 18:04:22.68 | 51.33 | 100.72 | 22.8 | 5.0 | 0.35 | 1622 | 3.61 | 0.43 | 0.10 | 0.35 |
51 | 13.07.2016 | 06:45:48.63 | 49.93 | 89.77 | 31.2 | 4.9 | 0.28 | 1462 | 3.93 | 0.47 | 0.09 | 0.38 |
52 | 20.09.2016 | 07:18:14.06 | 49.90 | 88.06 | 18.7 | 4.8 | 0.23 | 1318 | 4.35 | 0.52 | 0.08 | 0.42 |
53 | 04.04.2017 | 15:07:31.43 | 47.28 | 85.08 | 32.6 | 5.3 | 0.96 | 2213 | 3.89 | 0.47 | 0.14 | 0.38 |
54 | 01.02.2019 | 21:54:43.19 | 46.78 | 83.39 | 26.0 | 5.0 | 0.46 | 1622 | 4.67 | 0.56 | 0.10 | 0.45 |
55 | 29.03.2019 | 23:22:06.97 | 51.65 | 101.57 | 21.9 | 4.8 | 0.20 | 1318 | 3.90 | 0.47 | 0.08 | 0.38 |
56 | 13.09.2019 | 04:08:04.81 | 50.57 | 87.45 | 20.7 | 5.1 | 0.63 | 1799 | 4.70 | 0.56 | 0.11 | 0.46 |
57 | 21.09.2020 | 18:05:00.13 | 51.85 | 103.50 | 25.9 | 5.5 | 2.49 | 2723 | 5.40 | 0.65 | 0.17 | 0.52 |
58 | 21.09.2020 | 18:19:58.18 | 51.80 | 103.48 | 18.5 | 4.8 | 0.20 | 1318 | 3.74 | 0.45 | 0.08 | 0.36 |
59 | 11.01.2021 | 21:33:07.45 | 51.32 | 100.39 | 13.9 | 6.8 | 190.00 | 10471 | 7.24 | 0.87 | 0.66 | 0.70 |
60 | 13.01.2021 | 11:10:11.81 | 51.63 | 100.61 | 12.0 | 4.8 | 0.18 | 1318 | 3.48 | 0.42 | 0.08 | 0.34 |
61 | 21.02.2021 | 01:37:08.94 | 52.33 | 97.44 | 27.4 | 5.0 | 0.36 | 1622 | 3.73 | 0.45 | 0.10 | 0.36 |
62 | 31.03.2021 | 00:01:29.29 | 51.24 | 100.45 | 24.9 | 5.3 | 1.02 | 2213 | 4.12 | 0.49 | 0.14 | 0.40 |
63 | 03.05.2021 | 08:46:41.95 | 51.31 | 100.43 | 27.5 | 5.7 | 4.21 | 3350 | 4.90 | 0.59 | 0.21 | 0.48 |
64 | 06.09.2021 | 07:47:21.91 | 53.20 | 99.23 | 24.9 | 5.3 | 1.05 | 2213 | 4.24 | 0.51 | 0.14 | 0.41 |
65 | 22.10.2021 | 23:03:04.95 | 51.39 | 91.67 | 29.8 | 5.0 | 0.42 | 1622 | 4.28 | 0.51 | 0.10 | 0.42 |
66 | 29.07.2022 | 13:01:14.18 | 50.40 | 90.70 | 13.0 | 5.5 | 2.37 | 2723 | 5.14 | 0.62 | 0.17 | 0.50 |
67 | 14.01.2023 | 07:39:34.60 | 51.08 | 100.03 | 19.9 | 4.9 | 0.26 | 1462 | 3.67 | 0.44 | 0.09 | 0.36 |
68 | 04.03.2023 | 01:18:25.17 | 51.04 | 98.28 | 19.7 | 4.8 | 0.17 | 1318 | 3.27 | 0.39 | 0.08 | 0.32 |
69 | 15.02.2025 | 01:48:13.11 | 50.03 | 88.24 | 26.0 | 5.8 | 6.20 | 3715 | 5.29 | 0.63 | 0.23 | 0.51 |
Список литературы
1. Abdrakhmatov K.Ye., Aldazhanov S.A., Hager B.H., Hamburger M.W., Herring T.A., Kalabaev K.B., Makarov V.I., Molnar P. et al., 1996. Relatively Recent Construction of the Tien Shan Inferred from GPS Measurements of Present-Day Crustal Deformation Rates. Nature 384, 450–453. https://doi.org/10.1038/384450a0.
2. Айвазян С.А. Прикладная статистика. Основы эконометрики. Т. 2. Основы эконометрики: Учебник. М.: Юнити-Дана, 2001. 432 с.
3. Айвазян С.А., Мхитарян В.С. Прикладная статистика. Основы эконометрики. Т. 1. Теория вероятностей и прикладная статистика: Учебник. М.: Юнити-Дана, 2001. 656 с.
4. Аптекман Ж.Я., Белавина Ю.Ф., Захарова А.И., Зобин В.М., Коган С.Я., Корчагина О.А., Москвина А.Г., Поликарпова Л.А., Чепкунас Л.С. Спектры Р-волн в задаче определения динамических параметров очагов землетрясений. Переход от станционного спектра к очаговому и расчет динамических параметров очага // Вулканология и сейсмология. 1989. № 2. С. 66–79.
5. Бачманов Д.М., Кожурин А.И., Трифонов В.Г. База данных активных разломов Евразии // Геодинамика и тектонофизика. 2017. Т. 8. № 4. С. 711–736. https://doi.org/10.5800/GT-2017-8-4-0314.
6. Boore D., 2003. Simulation of Ground Motion Using the Stochastic Method. Pure and Applied Geophysics 160 (3–4), 635–676. https://doi.org/10.1007/PL00012553.
7. Bormann P., Liu R., Xu Z., Ren K., Zhang L., Wendt S., 2009. First Application of the New IASPEI Teleseismic Magnitude Standards to Data of the China National Seismographic Network. Bulletin of the Seismological Society of America 99 (3), 1868–1891. https://doi.org/10.1785/0120080010.
8. Brune J.N., 1970. Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes. Journal of Geophysical Research 75 (26), 4997–5009. https://doi.org/10.1029/JB075i026p04997.
9. Brune J.N., 1971. Correction [to "Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes"]. Journal of Geophysical Research 76 (20), 5002. https://doi.org/10.1029/JB076i020p05002.
10. Чепкунас Л.С., Малянова Л.С. Очаговые параметры сильных землетрясений Земли // Землетрясения Северной Евразии. Обнинск: ФИЦ ЕГС РАН, 2017. Вып. 20 (2011 г.). С. 277–281.
11. Чепкунас Л.С., Малянова Л.С. Очаговые параметры сильных землетрясений Земли // Землетрясения Северной Евразии. Обнинск: ФИЦ ЕГС РАН, 2018. Вып. 21 (2012 г.). С. 280–285.
12. Chinnery V.A., 1961. The Deformation of the Ground Around Surface Faults. Bulletin of the Seismological Society of America 51 (3), 355–3725. https://doi.org/10.1785/BSSA0510030355.
13. Chinnery V.A., 1969. Earthquake Magnitude and Source Parameters. Bulletin of the Seismological Society of America 59 (5), 1969–1982. https://doi.org/10.1785/BSSA0590051969.
14. Dobrynina A.A., 2009. Source Parameters of the Earthquakes of the Baikal Rift System. Izvestiya, Physics of the Solid Earth 45 (12), 1093–1109. https://doi.org/10.1134/S1069351309120064.
15. Emanov A.F., Emanov A.A., Chechel’nitskii V.V., Shevkunova E.V., Radziminovich Ya.B., Fateev A.V., Kobeleva E.A., Gladyshev E.A., Arapov V.V., Artemova A.I., Podkorytova V.G., 2022. The Khuvsgul Earthquake of January 12, 2021 (MW=6.7, ML=6.9) and Early Aftershocks. Izvestiya, Physics of the Solid Earth 58, 59–73. https://doi.org/10.1134/S1069351322010025.
16. Еманов А.Ф., Еманов А.А., Чечельницкий В.В., Шевкунова Е.В., Кобелева Е.А., Фатеев А.В. Блоковая структура и сильнейшие землетрясения стыка Алтае-Саянской области и Байкальской рифтовой зоны // Проблемы комплексного геофизического мониторинга сейсмоактивных регионов: Труды Девятой всероссийской научно-технической конференции с международным участием (24–30 сентября 2023 г.). Петропавловск-Камчатский: КФ ФИЦ ЕГС РАН, 2023. С. 139–142.
17. Еманов А.Ф., Еманов А.А., Фатеев А.В., Соловьев В.М., Шевкунова Е.В., Гладышев Е.А., Антонов И.А., Корабельщиков Д.Г. и др. Сейсмологические исследования на территории Алтае-Саянской горной области // Российский сейсмологический журнал. 2021. Т. 3. № 2. С. 20–51. https://doi.org/10.35540/2686-7907.2021.2.02.
18. Еманов А.Ф., Еманов А.А., Лескова Е.В. Сейсмические активизации в Белино-Бусингольской зоне // Физическая мезомеханика. 2010. Т. 13. № S1. С. 72–77.
19. Emanov A.F., Emanov A.A., Leskova E.V., Seleznev V.S., Fateev A.V., 2014a. The Tuva Earthquakes of December 27, 2011, ML=6.7, and February 26, 2012, ML=6.8, and Their Aftershocks. Doklady Earth Sciences 456 (1), 594–597. https://doi.org/10.1134/S1028334X14050249.
20. Еманов А.Ф., Лескова Е.В., Еманов А.А., Радзиминович Я.Б., Гилёва Н.А., Артёмова А.И. Белин-Бий-Хемское землетрясение 16 августа 2008 г. с КР=15, МW=5.7, I0=7 (Республика Тыва) // Землетрясения Северной Евразии. Обнинск: ГС РАН, 2014. Вып. 17 (2008 г.). С. 378–385.
21. Kanamori H., 1977. The Energy Release in Great Earthquakes. Journal of Geophysical Research 82 (20), 2981–2987. https://doi.org/10.1029/JB082i020p02981.
22. Kaneko Y., Shearer P.M., 2014. Seismic Source Spectra and Estimated Stress Drop Derived from Cohesive-Zone Models of Circular Subshear Rupture. Geophysical Journal International 197 (2), 1002–1015. https://doi.org/10.1093/gji/ggu030.
23. Kim W.-Y., Wahlström R., Uski M., 1989. Regional Spectral Scaling Relations of Source Parameters for Earthquakes in the Baltic Shield. Tectonophysics 166 (1–3), 151–161. https://doi.org/10.1016/0040-1951(89)90210-2.
24. Кочарян Г.Г. Об излучательной эффективности землетрясений (пример геомеханической интерпретации результатов сейсмологических наблюдений) // Динамические процессы в геосферах. 2012. № 3. С. 36–47.
25. Кочарян Г.Г. Масштабный эффект в сейсмотектонике // Геодинамика и тектонофизика. 2014. Т. 5. № 2. С. 353–385. https://doi.org/10.5800/GT-2014-5-2-0133.
26. Кочарян Г.Г. Геомеханика разломов. М.: ГЕОС, 2016. 424 с..
27. Костров Б.В. Механика очага тектонического землетрясения. М.: Наука, 1975. 176 с.
28. Кучай О.А. Особенности поля напряжений афтершоковых процессов землетрясений Алтае-Саянской горной области // Геодинамика и тектонофизика. 2012. Т. 3. № 1. С. 59–68. https://doi.org/10.5800/GT-2012-3-1-0062.
29. Larson K.M., Bürgmann R., Bilham R., Freymueller J.T., 1999. Kinematics of the India-Eurasia Collision Zone from GPS Measurements. Journal of Geophysical Research: Solid Earth 104 (B1), 1077–1093. https://doi.org/10.1029/1998JB900043.
30. Сейсмотектоника и сейсмичность Прихубсугулья / Ред. Н.А. Логачев. Новосибирск: Наука, 1993. 184 с.
31. Лукк А.А., Юнга С.Л. Сейсмотектоническая деформация Гармского района // Известия АН СССР. Физика Земли. 1979. № 10. С. 24–43.
32. Madariaga R., 2011. Earthquake Scaling Laws. In: R. Meyers (Ed.), Extreme Environmental Events: Complexity in Forecasting and Early Warning. Springer, New York, p. 364–383. https://doi.org/10.1007/978-1-4419-7695-6_22.
33. Мишарина Л.А., Мельникова В.И., Балжинням И. Юго-западная граница Байкальской рифтовой зоны по данным о механизме очагов землетрясений // Вулканология и сейсмология. 1983. № 2. С. 74–83.
34. Ризниченко Ю.В. Проблемы сейсмологии. М.: Наука, 1985. 408 с.
35. Саньков В.А., Леви К.Г., Лухнев А.В., Мирошниченко А.И., Парфеевец А.В., Радзиминович Н.А., Мельникова В.И., Девершер Ж. и др. Современная геодинамика Монголо-Сибирского подвижного пояса по данным геолого-структурных и инструментальных исследований // Тектоника и геофизика литосферы: Материалы XXXV Тектонического совещания (1 января – 31 декабря 2002 г.). М.: ГЕОС, 2002. Т. 2. С. 170–174.
36. Sankov V.A., Lukhnev A.V., Miroshnichenko A.I., Levi K.G., Ashurkov S.V., Bashkuev Yu.B., Dembelov M.G., Calais E. et al., 2003. Present-Day Movements of the Earth’s Crust in the Mongol-Siberian Region Inferred from GPS Geodetic Data. Doklady Earth Sciences 393 (8), 1082–1085.
37. Scholz C.H., 2002. The Mechanics of Earthquakes and Faulting. Cambridge University Press, Cambridge, 496 p. https://doi.org/10.1017/CBO9780511818516.
38. Сычева Н.А. Исследование сейсмотектонических деформаций земной коры Алтае-Саянской горной области. Часть I // Геосистемы переходных зон. 2023. Т. 7. № 3. С. 223–242. https://doi.org/10.30730/gtrz.2023.7.3.223-242.
39. Sycheva N.A., Bogomolov L.M., 2016. Patterns of Stress Drop in Earthquakes of the Northern Tien Shan. Russian Geology and Geophysics 57 (11), 1635–1645. https://doi.org/10.1016/j.rgg.2016.10.009.
40. Sycheva N.A., Bogomolov L.M., 2020. On the Stress Drop in North Eurasia Earthquakes Source Versus Specific Seismic Energy. Geosystems of Transition Zones 4 (4), 393–446. https://doi.org/10.30730/gtrz.2020.4.4.393-416.417-446.
41. Сычева Н.А., Богомолов Л.М., Кузиков С.И. Вычислительные технологии в сейсмологических исследованиях (на примере KNET, Северный Тянь-Шань). Южно-Сахалинск: ИМГиГ ДВО РАН, 2020. 358 с. https://doi.org/10.30730/978-5-6040621-6-6.2020-2.
42. Сычева Н.А., Ребецкий Ю.Л. Сравнение некоторых оценок деформации земной коры Алтае-Саянской горной области, полученных на основе методов СТД и МКА // Тектонофизика и актуальные вопросы наук о Земле: Материалы Шестой тектонофизической конференции, приуроченной к 300-летию Российской академии наук (7–12 октября, 2024 г.). М.: ИФЗ РАН, 2024. С. 329–336.
43. Сычева Н.А., Сычев В.Н. Некоторые характеристики сейсмичности Алтая и Саян // Проблемы геокосмоса – 2022: Материалы XIV школы-конференции с международным участием (3–7 октября 2022 г.). СПб.: Скифия-принт, 2022. C. 84–92.
44. Ваков А.В. Соотношения магнитуды и размеров очагов землетрясений при различных типах подвижек // Сборник научных трудов Гидропроекта. М.: Энергоиздат, 1988. Вып. 130. С. 55–69.
45. Захарова А.И., Чепкунас Л.С., Малянова Л.С. Очаговые параметры сильных землетрясений Земли // Землетрясения Северной Евразии. Обнинск: ГС РАН, 2009. Вып. 12 (2003 г.). С. 255–260.
46. Zavyalov A.D., Zotov O.D., 2021. A New Way to Determine the Characteristic Size of the Source Zone. Journal of Volcanology and Seismology 15 (1), 19–25. https://doi.org/10.1134/S0742046321010139.
Об авторах
Н. А. СычеваРоссия
123242, Москва, ул. Большая Грузинская, 10, стр. 1
Л. М. Богомолов
Россия
693022, Южно-Сахалинск, ул. Науки, 1Б
Рецензия
Для цитирования:
Сычева Н.А., Богомолов Л.М. РАСПРЕДЕЛЕНИЕ ПРИВЕДЕННОЙ СЕЙСМИЧЕСКОЙ ЭНЕРГИИ И СБРОШЕННЫХ НАПРЯЖЕНИЙ В АЛТАЕ-САЯНСКОМ СЕЙСМОАКТИВНОМ РЕГИОНЕ. Геодинамика и тектонофизика. 2025;16(4):0835. https://doi.org/10.5800/GT-2025-16-4-0835. EDN: VWPTKO
For citation:
Sycheva N.A., Bogomolov L.M. DISTRIBUTION OF REDUCED SEISMIC ENERGY AND STRESS DROP IN THE ALTAI-SAYAN SEISMOACTIVE REGION. Geodynamics & Tectonophysics. 2025;16(4):0835. https://doi.org/10.5800/GT-2025-16-4-0835. EDN: VWPTKO
JATS XML




















































