Перейти к:
РАНЖИРОВАНИЕ ЗАКОНОВ ЗАТУХАНИЯ ИНТЕНСИВНОСТИ СЕЙСМИЧЕСКИХ ВОЗДЕЙСТВИЙ И ПОСТРОЕНИЕ МОДЕЛЕЙ СЕЙСМИЧЕСКИХ ИСТОЧНИКОВ ПРИ ОЦЕНКЕ СЕЙСМИЧЕСКОЙ ОПАСНОСТИ ТЕРРИТОРИИ УЗБЕКИСТАНА
https://doi.org/10.5800/GT-2024-15-4-0770
EDN: PEIYOD
Аннотация
Количественные оценки сейсмической опасности сейсмоактивных территорий в значительной степени зависят от выбора законов затухания сейсмических воздействий с расстоянием, используемых в расчетах. Для учета эпистемических неопределенностей в характере сейсмических воздействий в практике вероятностного анализа сейсмической опасности рекомендуется использование нескольких различных зависимостей затухания. Наиболее эффективным инструментом их отбора является процедура ранжирования, состоящая в придании веса тому или иному уравнению в зависимости от степени соответствия прогнозируемых на его основе сейсмических воздействий реальным экспериментальным данным, имеющимся для исследуемого региона.
В статье приведены результаты ранжирования законов затухания интенсивности сейсмических воздействий, разработанных для территории Центральной Азии. Ранжирование проводилось методами LH и LLH. По результатам ранжирования построена обобщенная модель затухания, которая впоследствии используется для ВАСО территории Узбекистана. В качестве моделей сейсмических источников рассматривались три альтернативные модели: площадные источники, активные разломы земной коры и сейсмогенные зоны. Проведена параметризация рассматриваемых моделей, включающая определение сейсмического потенциала, частоты повторения землетрясений различного энергетического уровня, преобладающего кинематического типа подвижек в очагах землетрясений каждого источника. Для различных вероятностей непревышения уровня сейсмических воздействий в течение 50 лет построены карты сейсмического районирования территории Узбекистана в баллах макросейсмической шкалы MSK-64.
Ключевые слова
Для цитирования:
Ибрагимов Р.С., Ибрагимова Т.Л., Мирзаев М.А., Ашуров С.Х. РАНЖИРОВАНИЕ ЗАКОНОВ ЗАТУХАНИЯ ИНТЕНСИВНОСТИ СЕЙСМИЧЕСКИХ ВОЗДЕЙСТВИЙ И ПОСТРОЕНИЕ МОДЕЛЕЙ СЕЙСМИЧЕСКИХ ИСТОЧНИКОВ ПРИ ОЦЕНКЕ СЕЙСМИЧЕСКОЙ ОПАСНОСТИ ТЕРРИТОРИИ УЗБЕКИСТАНА. Геодинамика и тектонофизика. 2024;15(4):0770. https://doi.org/10.5800/GT-2024-15-4-0770. EDN: PEIYOD
For citation:
Ibragimov R.S., Ibragimova T.L., Mirzaev M.A., Ashurov S.H. RANKING OF SEISMIC INTENSITY ATTENUATION LAWS AND MODELING OF SEISMIC SOURCES FOR SEISMIC HAZARD ASSESSMENT IN UZBEKISTAN. Geodynamics & Tectonophysics. 2024;15(4):0770. https://doi.org/10.5800/GT-2024-15-4-0770. EDN: PEIYOD
1. ВВЕДЕНИЕ
Действующие в Узбекистане строительные нормы опираются на оценки сейсмической опасности в показателях макросейсмической интенсивности. В 2017 г. в рамках вероятностно-детерминистического подхода к оценке сейсмической опасности [Riznichenko, 1985; Riznichenko, Seiduzova, 1984] был разработан комплект карт сейсмического районирования территории республики ОСР-2017 [Artikov et al., 2018, 2020а]. В этих картах для различных вероятностей Р (Р=0.90; Р=0.95; Р=0.98 и Р=0.99) непревышения уровня сейсмических воздействий в течение 50 лет сейсмическая опасность выражалась в баллах макросейсмической шкалы, скоростях и ускорениях колебаний грунта. В качестве нормативной карты общего сейсмического районирования территории Узбекистана Министерством строительства РУз в 2019 г. была утверждена карта сейсмической опасности в баллах шкалы MSK-64, отвечающая вероятности Р=0.98 непревышения уровня сейсмических воздействий в течение 50 лет (период повторяемости 2500 лет). Фрагмент нормативной карты сейсмического районирования для территории, по которой проводилось данное исследование, приведен на рис. 1.
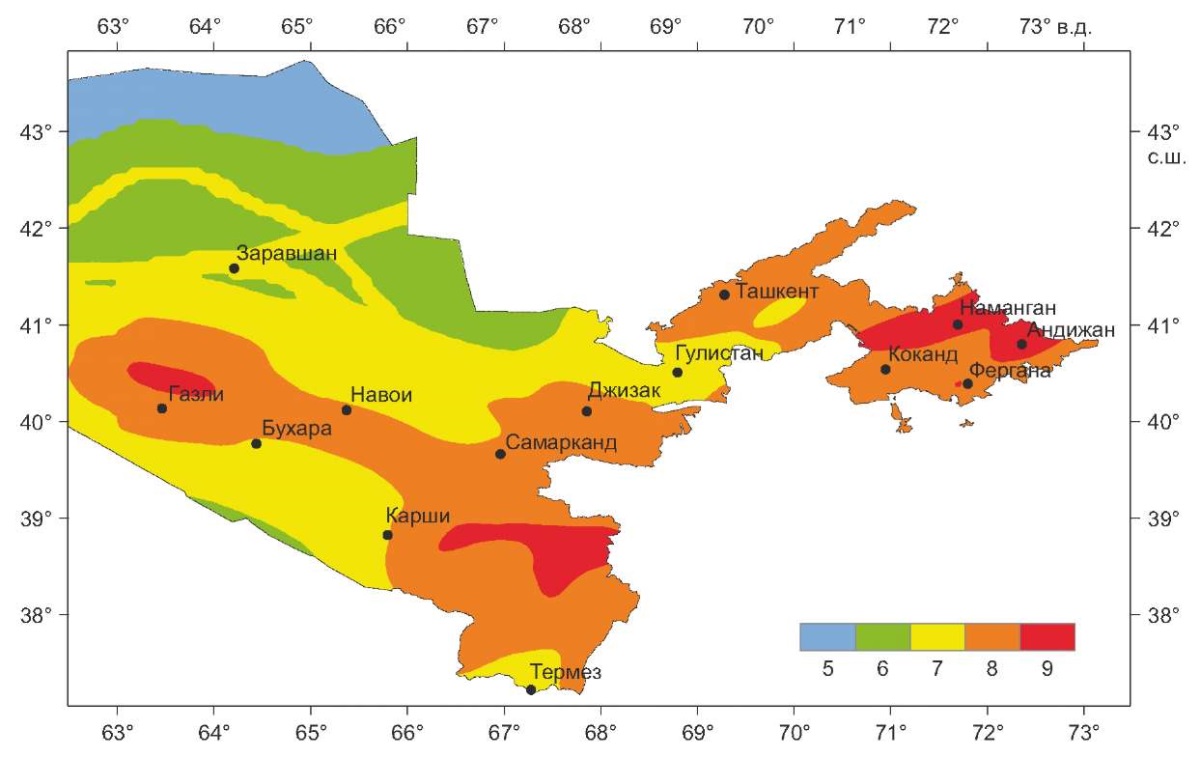
Рис. 1. Фрагмент нормативной карты общего сейсмического районирования территории Узбекистана ОСР-2017.
Fig. 1. A fragment of the general normative seismic zoning map GSZ-2017 for Uzbekistan.
Сопоставление вероятностно-детерминистического подхода, основанного на теории макросейсмической и спектрально-временной сотрясаемости [Riznichenko, 1985; Riznichenko, Seiduzova, 1984], и классического вероятностного подхода, опирающегося на теорему о полной вероятности [Cornell, 1968; McGuire, 2004; и др.], проведено во множестве исследований (например [Chernov, 1989; Bindi et al., 2011; Ibragimov et al., 2022b; и др.]). В указанных работах отмечается, что в рамках подхода Ю.В. Ризниченко расчет опасности проводится при средних значениях параметров сейсмического режима каждого источника, без учета их вариабельности, и при медианных значениях в законах затухания сейсмических воздействий, без учета алеаторной изменчивости в уравнениях движения грунта. Это приводит к недооценке сейсмической опасности сейсмоактивных территорий. В статье [Ibragimov et al., 2022b] проведено сопоставление оценок, получаемых при реализации названных подходов, для территории Узбекистана. Показано, что разница в оценках опасности в зависимости от выбранного подхода возрастает с увеличением требуемой вероятности непревышения уровня сейсмического воздействия в течение заданного промежутка времени и для объектов строительства с высокой категорией ответственности становится весьма существенной.
Оценки сейсмической опасности сейсмоактивных территорий в значительной степени зависят от выбора законов затухания сейсмических воздействий с расстоянием, используемых в расчетах [Artikov et al., 2016; Bykova, Tatevosyan, 2015; и др.]. Прогнозируемый сейсмический эффект, определяемый по различным уравнениям движения грунта, полученным даже по одной и той же совокупности экспериментальных данных, может быть существенно разным. Эти различия в значительной степени обусловлены заложенной в конкретное уравнение формой связи между уровнем сейсмического воздействия и магнитудой землетрясения, его механизмом, расстоянием до пункта, для которого оценивается опасность, и грунтовыми условиями этого пункта. При этом усложнение формы уравнения далеко не всегда приводит к улучшению прогнозируемого на его основе сейсмического эффекта. Для учета эпистемических неопределенностей в параметрах движения грунта в практике вероятностного анализа сейсмической опасности (ВАСО) рекомендуется использование нескольких различных уравнений затухания. Простое увеличение числа привлекаемых уравнений, как правило, не решает данную задачу. Наиболее эффективным инструментом ее решения является процедура ранжирования, состоящая в придании веса тому или иному уравнению, в зависимости от степени соответствия прогнозируемых на его основе сейсмических воздействий реальным экспериментальным данным, имеющимся для исследуемого региона. В данном исследовании ранжирование моделей затухания интенсивности сейсмических воздействий с расстоянием, разработанных для территории Центральной Азии, проводилось двумя различными методами – LH [Scherbaum et al., 2004] и LLH [Scherbaum et al., 2009]. С учетом проведенной процедуры ранжирования построена обобщенная модель затухания, которая впоследствии используется для получения вероятностных оценок сейсмической опасности территории Узбекистана в баллах макросейсмической шкалы MSK-64.
2. АНАЛИЗИРУЕМЫЕ ЗАВИСИМОСТИ ЗАТУХАНИЯ ИНТЕНСИВНОСТИ СЕЙСМИЧЕСКИХ ВОЗДЕЙСТВИЙ С РАССТОЯНИЕМ
Для оценки сейсмической опасности территории Узбекистана в значениях макросейсмической интенсивности было отобрано несколько уравнений затухания интенсивности сейсмических воздействий с расстоянием. Наряду с зависимостью Н.В. Шебалина [Shebalin, 1968, 1972], полученной по мировым данным,
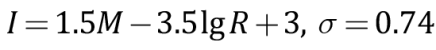 (1)
(1)
рассматривались еще несколько зависимостей, приведенных в статье [Artikov et al., 2020b], которые были получены на основе анализа схем изосейст сильных землетрясений Центральной Азии:
– зависимость типа Блейка-Шебалина:
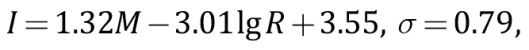 (2)
(2)
– зависимость типа Ковеслигети [Kovesligethy, 1907]:
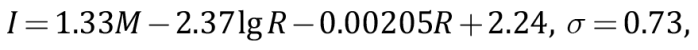 (3)
(3)
– зависимость, в которой коэффициент затухания зависит от глубины очага землетрясения:
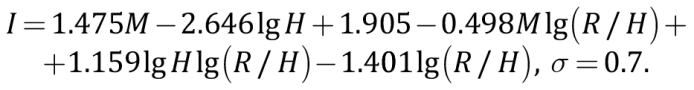 (4)
(4)
К анализу была привлечена также зависимость Д. Бинди [Bindi et al., 2011], полученная несколько ранее по макросейсмическим данным Центрально-Азиатского региона:
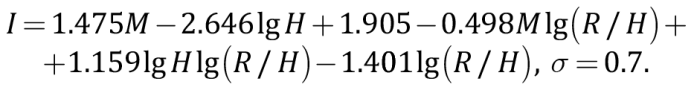 (5)
(5)
Во всех приведенных выше зависимостях в качестве расстояния R используется гипоцентральное расстояние Rhyp, а в качестве магнитуды M – магнитуда MS.
Следует подчеркнуть, что хотя зависимости (5) и (2–4) получены по макросейсмичеким данным практически одних и тех же землетрясений Центральной Азии, исходная информация для их построения была все же несколько различной. В первом случае использовались таблицы «пункты – баллы», во втором – размеры изосейст различной макросейсмической интенсивности при каждом землетрясении.
3. РАНЖИРОВАНИЕ ЗАВИСИМОСТЕЙ ЗАТУХАНИЯ
3.1. Ранжирование зависимостей затухания методом LH
Пусть задан закон затухания интенсивности сейсмических воздействий с расстоянием, определяющий для каждой пары (M, R) (магнитуда – расстояние) значение интенсивности сейсмического воздействия I=I(M, R) со стандартной ошибкой σ.
Пусть Iobs – экспериментальное значение интенсивности, зарегистрированное на расстоянии R от очага землетрясения с магнитудой M, а α – значение интенсивности для той же пары (M, R), предсказанное по выбранному закону затухания I=I(M, R). Предметом анализа является выборка нормированных на величину стандартного отклонения σ значений центрированных разностей между наблюденными и прогнозируемыми значениями сейсмического воздействия:
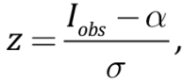 (6)
(6)
которые иногда называют нормализованными невязками. В рамках подхода, использованного в статье [Scherbaum et al., 2004], для исследования степени пригодности той или иной модели, описывающей движение грунта при землетрясениях, к региону, для которого имеется ограниченный набор экспериментальных данных, проводится сравнение частот нормализованных невязок с частотами, которые можно было бы ожидать при условии распределения этих невязок по нормальному закону с нулевым средним значением и единичной дисперсией. Оценивается вероятность того, что абсолютное значение случайной величины из нормализованного распределения попадет в интервал между модулем конкретного наблюдения z0 и ∞.
Для положительного значения z0 это будет
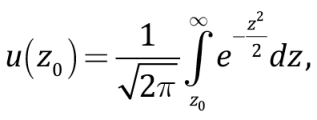 (7)
(7)
u(z0) может быть выражено как
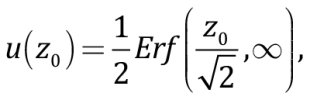 (8)
(8)
где Erf(z) – интеграл ошибок 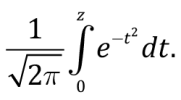
Рассматривая оба хвоста распределения, параметр LH по отношению к наблюдению z0 можно определить как
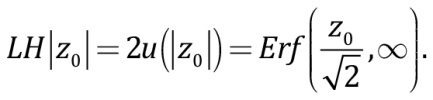 (9)
(9)
В совокупности со статистическими свойствами выборки нормализованных невязок {Z} (среднее, медиана, величина среднеквадратического отклонения) статистические характеристики распределения величины LH позволяют судить о степени соответствия различных моделей движения грунта заданному набору экспериментальных данных [Scherbaum et al., 2004]. Отклонение среднего и медианы нормализованных невязок от нуля, а также отклонение стандартного отклонения от единицы помогают выявить слабые модели. Большие различия между средним значением и медианой нормализованных невязок должны помочь выявить модели, для которых распределение остатков перекошено.
В статье [Scherbaum et al., 2004] проводится следующая классификация моделей уравнений движения грунта (GMPE), по степени применимости к исследуемому региону.
Модель класса A (модель, наилучшим образом соответствующая экспериментальным данным) характеризуется минимальным значением медианы LH=0.4 и абсолютным значением среднего и медианы нормализованных невязок 0.25. Стандартное отклонение выборки нормализованных невязок должно быть менее 1.125.
Модель класса B (приемлемая модель) характеризуется минимальным значением медианы LH=0.3 и абсолютным значением среднего и медианы нормализованных невязок менее 0.5. Стандартное отклонение выборки нормализованных невязок должно быть менее 1.25.
Модель класса C (минимально приемлемая модель) характеризуется минимальным значением медианы LH=0.2 и абсолютным значением среднего и медианы нормализованных невязок менее 0.75. Стандартное отклонение выборки нормализованных невязок должно быть менее 1.5.
Если модель не удовлетворяет ни одному из приведенных выше критериев, то она признается неудовлетворительной – класс D.
На рис. 2 показано распределение нормализованных невязок и величины LH для пяти рассматриваемых законов затухания, а в табл. 1 приведены результаты ранжирования тестируемых моделей.

Рис. 2. Распределение нормализованных невязок Z (левая колонка) и величины LH (правая колонка) для пяти рассматриваемых законов затухания.
Fig. 2. Distribution of the normalized residuals Z (left column) and LH values (right column) for the five attenuation laws considered.
Таблица 1. Ранжирование моделей затухания интенсивности
сейсмических воздействий с расстоянием методом LH
Table 1. Intensity-distance attenuation model ranking by the LH method
Модель затухания | LH (медиана) | Параметры выборки нормализованных невязок {Z} | Ранг модели | ||
Медиана | Среднее | Стандартное отклонение | |||
1 | 0.493 | 0.129 | 0.094 | 1.118 | A |
2 | 0.477 | –0.410 | –0.425 | 1.050 | B |
3 | 0.522 | 0.012 | –0.002 | 1.046 | A |
4 | 0.527 | –0.014 | 0.001 | 1.010 | A |
5 | 0.401 | 0.669 | 0.755 | 1.106 | D |
Как это видно из табл. 1, наиболее приемлемыми для исследуемого региона являются модель Н.В. Шебалина (1) [Shebalin, 1968], модель типа Ковеслигети (3) [Artikov et al., 2020b] и модель (4), в которой коэффициент затухания зависит от глубины происходящих землетрясений [Artikov et al., 2020b]. Зависимость типа Блейка-Шебалина (2) [Artikov et al., 2020b] по классификации Ф. Шербаума [Scherbaum et al., 2004] отнесена к рангу B, что связано, в первую очередь, со смещением влево от нуля значений среднего и медианы нормализованных невязок. Это свидетельствует о систематическом завышении прогнозируемого макросейсмического эффекта. По этой же причине, но уже в связи с систематическим занижением прогнозируемого эффекта, худшие показатели среди тестируемых зависимостей дает зависимость Д. Бинди (5) [Bindi et al., 2011]. По классификации Ф. Шербаума [Scherbaum et al., 2004] эта модель относится к рангу D, и ее использование при оценке сейсмической опасности изучаемой территории не рекомендовано.
3.2. Ранжирование моделей затухания методом LLH
По мнению самих же разработчиков метода LH [Scherbaum et al., 2004], существенным недостатком данного подхода к ранжированию уравнений движения грунта является необходимость использования субъективных критериев, например порога приемлемости. Кроме того, результаты ранжирования уравнений движения грунта методом LH зависят от объема выборки, что также является его недостатком. В статье [Scherbaum et al., 2009] предлагается использовать более общий подход, который свободен от перечисленных недостатков. Суть данного метода в следующем.
Рассматриваются модели затухания g1, g2, g3 … gk, для каждой из которых известны функции плотности вероятности нормального распределения g1(x), g2(x), g3(x) … gk(x). Предполагается, что параметры плотности вероятности истинной модели затухания f неизвестны, но она также характеризуется нормальным распределением, и для нее известна выборочная совокупность наблюдений x={xi}, i=1, … N. В качестве критерия для ранжирования моделей затухания в статье [Scherbaum et al., 2009] предлагается использовать параметр LLH, определяемый для каждого закона затухания g как:
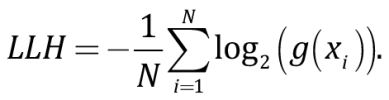 (10)
(10)
Таким образом, параметр LLH представляет собой нормированную на количество наблюдений N и взятую с отрицательным знаком функцию логарифмического правдоподобия функции g(x) относительно выборочной совокупности x={xi}. Чем меньше значения параметра LLH, тем ближе рассматриваемая модель затухания к выборочной совокупности. Считается [Scherbaum et al., 2009], что для хороших моделей затухания значения параметра LLH составляют примерно 1.4–1.6. Величину функционала LLH предлагается [Scherbaum et al., 2009] использовать для ранжирования моделей затухания путем присвоения веса wj различным моделям:
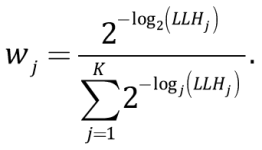 (11)
(11)
В нашем случае при нахождении параметра LLH для каждой модели затухания (1–5) и последующего ранжирования моделей выполнялась следующая процедура. Для каждого наблюденного значения интенсивности Iobs(i), которое зарегистрировано от землетрясения с магнитудой Mi на расстоянии Ri от эпицентра, рассматривалась функция плотности нормального распределения P(µ; σ)(x), в которой величина среднего значения µ равна интенсивности I(Mi, Ri), предсказанной по выбранному закону затухания, а σ – величина среднеквадратического отклонения в этом законе затухания. Определялось значение функции P(µ; σ)(x) в точке xi=Iobs(i). Обозначим его pi. По всей совокупности наблюденных интенсивностей Iobs(i), включающей N значений, параметр LLH для данного закона затухания определялся как:
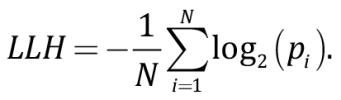 (12)
(12)
В табл. 2 представлены результаты ранжирования тестируемых моделей затухания методом LLH.
Таблица 2. Результаты ранжирования различных моделей затухания методом LLH
Table 2. Results of ranking different attenuation models by the LLH method
Номер зависимости | 1 | 2 | 3 | 4 | 5 |
Значение LLH | 1.7016 | 1.7109 | 1.5956 | 1.5454 | 2.0598 |
Вес к зависимостям | 0.200 | 0.200 | 0.213 | 0.221 | 0.166 |
Как это следует из табл. 2, согласно критерию LLH наиболее приемлемыми для исследуемой территории являются модели затухания (1–4), что в целом соответствует и ранжированию критерием LH.
Для построения обобщенной зависимости затухания модель 5 была отброшена как худшая по результатам ранжирования двумя рассмотренными критериями, и по значениям параметра LLH для первых четырех моделей был переопределен вес к зависимостям (1–4): w1=0.24, w2=0.24, w3=0.26, w4=0.26. С учетом найденных весовых коэффициентов построена обобщенная модель затухания, которая впоследствии используется для получения вероятностных оценок сейсмической опасности территории Узбекистана в показателях макросейсмической интенсивности.
4. МОДЕЛИ СЕЙСМИЧЕСКИХ ИСТОЧНИКОВ И ИХ СЕЙСМОЛОГИЧЕСКАЯ ПАРАМЕТРИЗАЦИЯ
Для вероятностного анализа сейсмической опасности территории Узбекистана были привлечены модели сейсмических источников трех типов: модель активных разломов земной коры, модель сейсмогенных зон и модель площадных источников.
Параметризация моделей сейсмических источников предполагает, наряду с определением геометрических характеристик каждого источника в плане и по глубине, нахождение его сейсмического потенциала, параметров повторяемости землетрясений различного энергетического уровня, кинематического типа подвижек в очагах происходящих в нем землетрясений и т.д. Остановимся на этом несколько подробнее.
Для построения модели источников в виде активных разломов земной коры использовалась база данных активных разломов Евразии (Active Fault Database of Eurasia – AFEAD) [Zelenin et al., 2022] (рис. 3, 4, 5). Для каждого разлома базы данных AFEAD имеются сведения о его морфологии, кинематике с количественными показателями позднечетвертичных смещений (три ранга). Разломы, присутствующие в базе данных, разделены на четыре класса (A, В, С, D) по степени выраженности (достоверности) проявления современной геодинамической активности – атрибут CONF. Таким образом, база данных AFEAD содержит в себе наиболее полные сведения, необходимые для проведения вероятностного анализа сейсмической опасности.
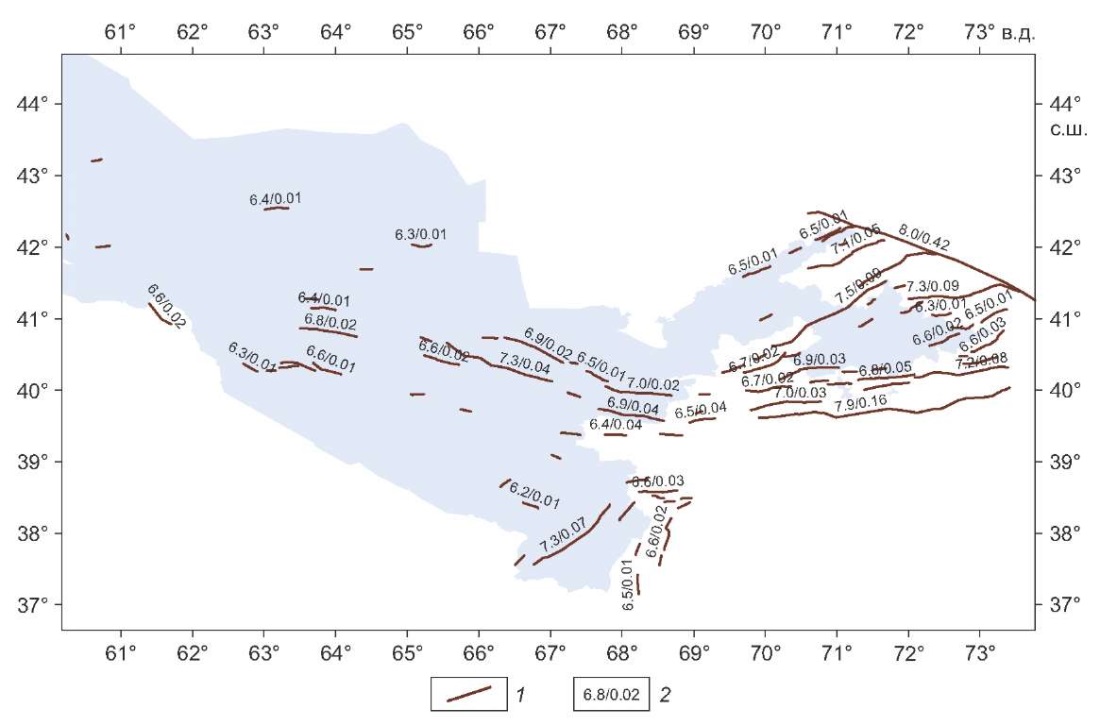
Рис. 3. Модель сейсмических источников в виде активных разломов земной коры с классом достоверности проявления современной геодинамической активности A+B. 1 – геометрия разлома; 2 – сейсмический потенциал (в числителе) и сейсмическая активность, приведенная к магнитуде М=5.0 (в знаменателе).
Fig. 3. A model of Class A and B active faults as seismic sources in accordance with the degree of modern geodynamic activity manifestation. 1 – fault geometry; 2 – seismic potential (in the numerator) and seismic activity reduced to magnitude M=5.0 (in the denominator).
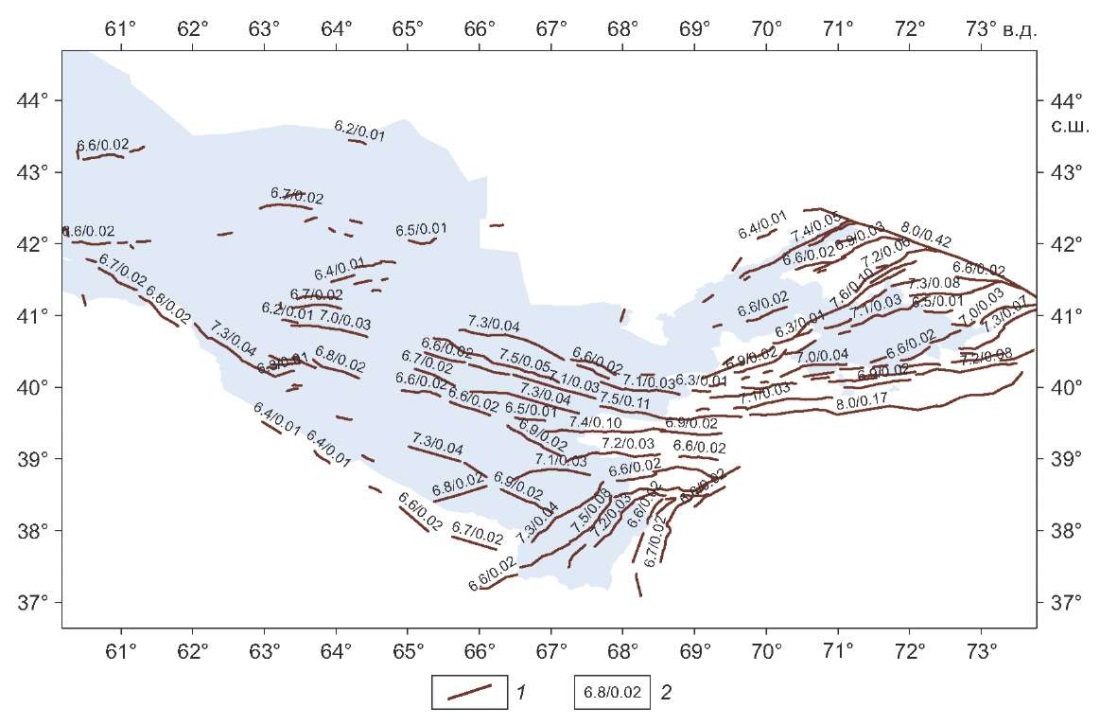
Рис. 4. Модель сейсмических источников в виде активных разломов земной коры с классом достоверности проявления современной геодинамической активности A+B+C. 1 – геометрия разлома; 2 – сейсмический потенциал (в числителе) и сейсмическая активность разлома, приведенная к магнитуде М=5.0 (в знаменателе).
Fig. 4. A model of Class A, B and C active faults as seismic sources in accordance with the degree of modern geodynamic activity manifestation. 1 – fault geometry; 2 – seismic potential (in the numerator) and seismic activity of the fault reduced to magnitude M=5.0 (in the denominator).
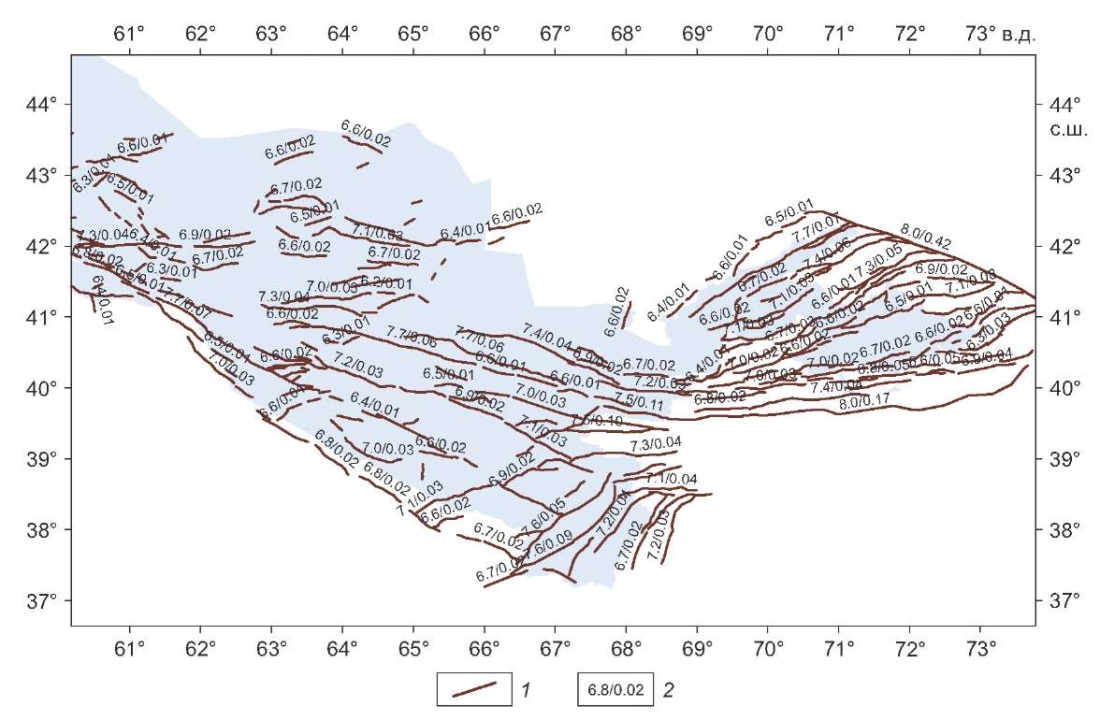
Рис. 5. Модель сейсмических источников в виде активных разломов земной коры с классом достоверности проявления современной геодинамической активности A+B+C+D. 1 – геометрия разлома; 2 – сейсмический потенциал (в числителе) и сейсмическая активность разлома, приведенная к магнитуде М=5.0 (в знаменателе).
Fig. 5. A model of Class A, B, C and D active faults as seismic sources in accordance with the degree of modern geodynamic activity manifestation. 1 – fault geometry; 2 – seismic potential (in the numerator) and seismic activity of the fault reduced to magnitude M=5.0 (in the denominator).
Геометрическая конфигурация модели сейсмогенных зон заимствована авторами работы из [Ibragimov et al., 2002]. Сейсмологическая параметризация данной модели, как и модели площадных источников, проводилась на базе регионального каталога землетрясений, включающего в себя сведения об исторических и инструментальных сейсмических событиях. Сведения о периодах представительности землетрясений различного магнитудного уровня в региональном каталоге, методах его декластеризации, уравнениях связи между различными типами магнитуд, использующиеся при ВАСО территории Узбекистана, можно найти в работах [Artikov et al., 2020a, 2020b; Ibragimov et al., 2022a, 2022b]. Карта эпицентров землетрясений, произошедших за исторический и инструментальный период наблюдений на исследуемой территории, по данным регионального каталога приведена на рис. 6. Врезками на рисунке показаны гистограммы распределения сейсмических событий различной магнитуды по глубине и график повторяемости землетрясений различной магнитуды (зависимость Гутенберга-Рихтера). Как это видно из гистограмм, подавляющая часть землетрясений с магнитудой М≥5.0 произошла в сейсмоактивном слое от 11 до 20 км. С учетом того, что именно этот диапазон магнитуд землетрясений создает наиболее значимые сейсмические воздействия, при расчете сейсмической опасности рассматривались три возможные глубины: H1=10 км, H2=15 км и H3=20 км, которые вошли в логическое дерево с весом w1=0.2, w2=0.6, w3=0.2. Угловой коэффициент графика повторяемости представительных землетрясений регионального каталога (b – параметр в зависимости Гутенберга-Рихтера lgN=a–bM) близок к единице.
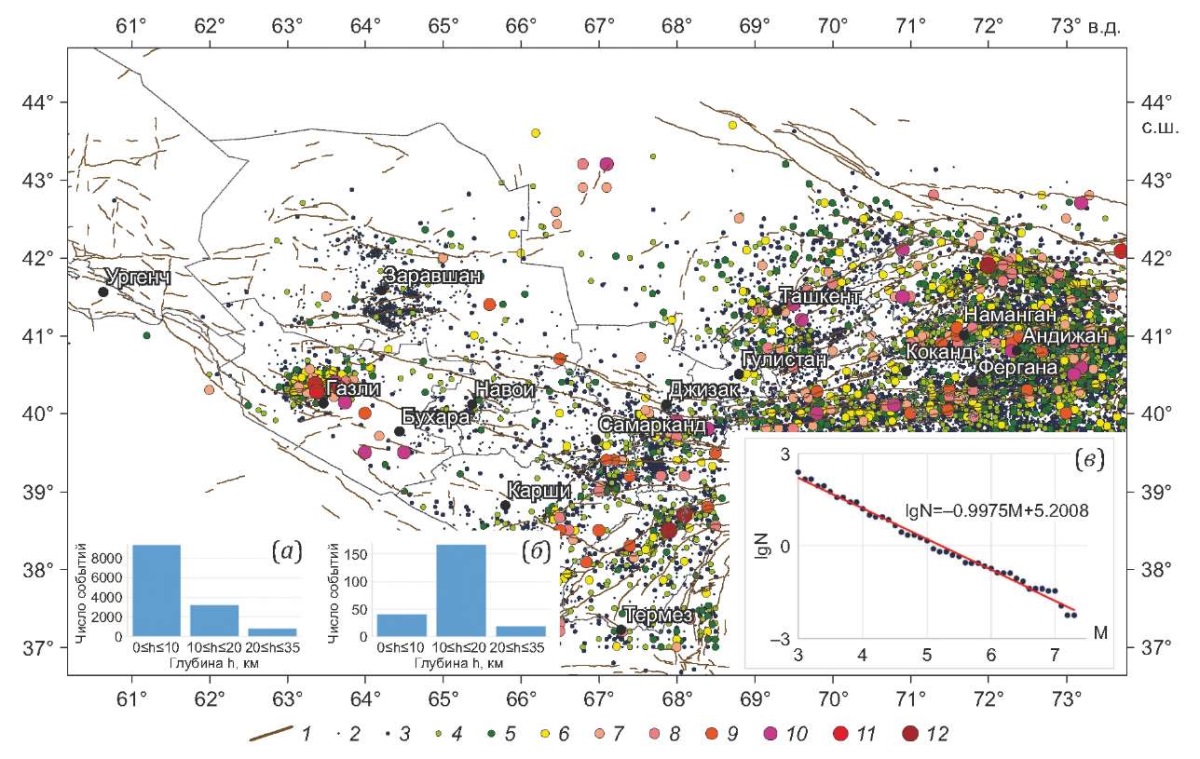
Рис. 6. Карта эпицентров землетрясений изучаемой территории за исторический и инструментальный период наблюдений, построенная по региональному каталогу.
Врезки (а, б) – гистограммы распределения представительных землетрясений каталога по глубине: (а) – землетрясения с магнитудой М<5.0; (б) – М≥5.0. Врезка (в) – график повторяемости землетрясений. 1 – активные разломы земной коры; 2–12 – землетрясения различной магнитуды: 2 – М<2.5, 3 – М=3.0, 4 – М=3.5, 5 – М=4.0, 6 – М=4.5, 7 – М=5.0, 8 – М=5.5, 9 – М=6.0, 10 – М=6.5, 11 – М=7.0, 12 – М>7.0.
Fig. 6. A map of earthquake epicenters in the study area for the historical and instrumental periods of observations, compiled from the regional catalog.
Insets (а, б) shows histograms of depth distribution of representative earthquakes from the catalog: (а) – earthquakes with magnitude M<5.0; (б) – M≥5.0. The inset (в) is a graph of earthquakes recurrence. 1 – active faults of Earth’s crust; 2–12 – earthquakes of different magnitudes: 2 – M<2.5, 3 – M=3.0, 4 – M=3.5, 5 – M=4.0, 6 – M=4.5, 7 – M=5.0, 8 – M=5.5, 9 – M=6.0, 10 – M=6.5, 11 – M=7.0, 12 – M>7.0.
4.1. Параметризация модели источников в виде активных разломов земной коры
Для оценки сейсмического потенциала активных разломов, как правило, используются соотношения, основанные на корреляции величины Мmax с геометрическими характеристиками тектонического нарушения (длина разлома L, длина максимального возможного на данном разломе поверхностного разрыва l, отвечающая этой длине ширина разрыва W, площадь максимального поверхностного разрыва A=l·W). В данном исследовании расчетное значение величины Мmax для каждого активного разлома земной коры определялось путем усреднения с равным весом оценок сейсмического потенциала по пяти различным зависимостям, полученным в работах [Hanks, Bakun, 2008; Leonard, 2010, 2014; Wells, Coppersmith, 1994], в которых величина Мmax выражается через длину разрыва l и его площадь A. При этом полагалось, что ширина разрыва W составляет половину от его длины W=l/2. Поскольку преобладающим кинематическим типом подвижки в очагах землетрясений территории Узбекистана является взброс [Ibragimova et al., 2021; Rebetsky et al., 2020], оценки величины Мmax по зависимостям [Hanks, Bakun, 2008; Leonard, 2010, 2014; Wells, Coppersmith, 1994] проводились для данного типа подвижки в очаге.
Следует сказать, что длина разрыва l, который может образоваться в случае возникновения землетрясения с максимальной магнитудой Мmax, составляет лишь определенный процент от всей протяженности разлома L. Исследование отношения l/L можно найти в ряде работ [Shteinberg, Ponomareva, 1987; Nowroozi, 1985; и др.]. В нашем исследовании это отношение было принято таким же, как в [Nowroozi, 1985].
Для оценки среднегодовой повторяемости землетрясений различной магнитуды N(M) в модели активных разломов земной коры применялись четыре соотношения, полученные в исследованиях [Anderson, Luco, 1983; Youngs, Coppersmith, 1985], и их программная реализация, описанная в [Bungum, 2007]. Зависимости [Anderson, Luco, 1983; Youngs, Coppersmith, 1985] для оценки повторяемости землетрясений различаются между собой характером высвобождения сейсмического момента, логарифм которого связан с магнитудой землетрясений линейной зависимостью. Значение сейсмической активности N(M), приведенное к магнитуде M=5.0, при расчете сейсмической опасности исследуемой территории находилось как среднее арифметическое по соотношениям, предложенным в работах [Anderson, Luco, 1983; Youngs, Coppersmith, 1985].
С учетом классов достоверности проявления современной геодинамической активности (атрибут CONF в базе данных AFEAD) было рассмотрено три варианта моделей сейсмических источников в виде активных разломов. В первом варианте рассматривались разломы с классами достоверности А и В. Во втором варианте учитывались разломы классов А, В и С. Наконец, в третьем, наиболее консервативном, варианте рассматривались разломы с классами достоверности А, В, С и D. На рис. 3, 4, 5 показана конфигурация трех рассмотренных выше моделей активных разломов земной коры на исследуемой территории. Там же в виде простой дроби для каждого разлома приведено значение сейсмического потенциала Мmax (в числителе) и среднегодовая частота возникновения землетрясений с магнитудой M≥5 (в знаменателе). Для каждой из трех рассмотренных моделей активных разломов в качестве параметра b (угловой коэффициент графика повторяемости землетрясений) принималось его региональное значение по каталогу землетрясений.
Модель разломов сама по себе недостаточно полна, чтобы охарактеризовать площадное распределение сейсмической активности в области малых магнитуд. Чтобы дополнить возможные отсутствующие события, в модель разломов добавлен фоновый слой источников, лимитированный максимальной магнитудой М=5.5. При этом полагалось, что землетрясения большой магнитуды приурочены к зонам активных разломов, которые должны фигурировать в базе данных активных разломов.
4.2. Модель источников в виде сейсмогенных зон
Сейсмогенная зона – это область активного динамического влияния крупного разлома или системы близко расположенных и одинаково направленных разрывов земной коры, которые на стадии тектонической активизации региона генерируют сильные землетрясения [Ibragimov et al., 2002]. На основе сейсмотектонических и сейсмологических данных [Ibragimov et al., 2002] на территории Узбекистана выделено порядка 30 сейсмогенерирующих зон с сейсмическим потенциалом Мmax≥5.5 (рис. 7).
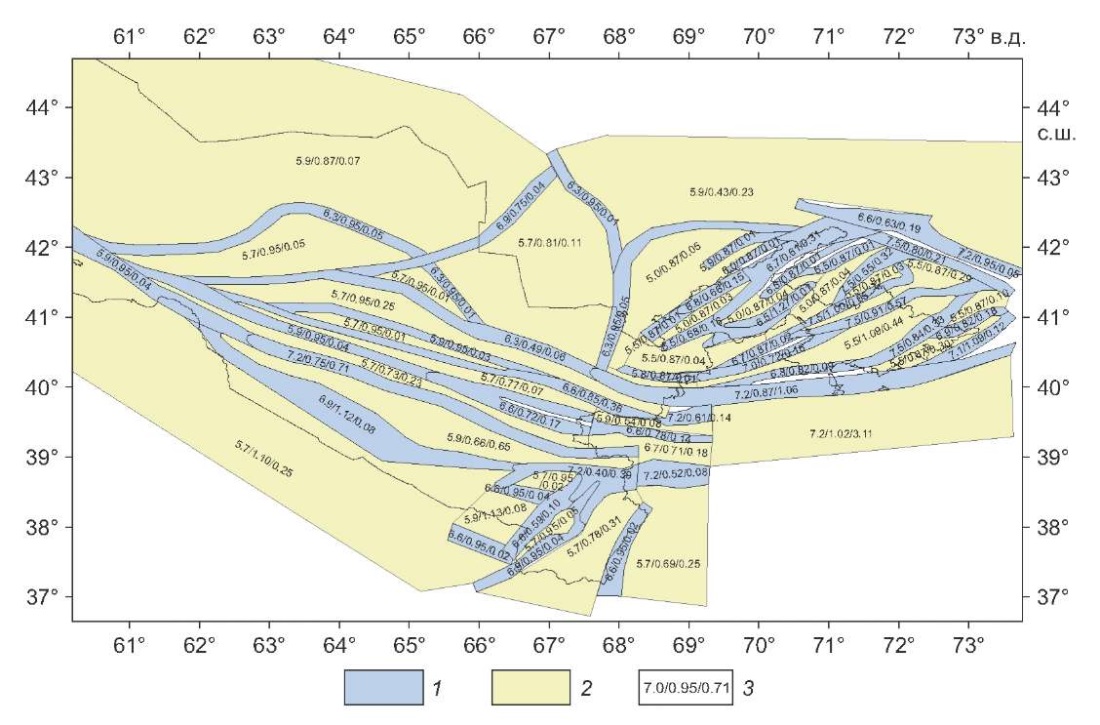
Рис. 7. Модель сейсмических источников в виде сейсмогенных зон для территории Узбекистана.
1 – сейсмогенные зоны; 2 – источники, расположенные вне сейсмогенных зон; 3 – оценки сейсмического потенциала Мmax, параметра b и сейсмической активности, приведенной к магнитуде М=4.0.
Fig. 7. A model of seismogenic zones as seismic sources for the territory of Uzbekistan.
1 – seismogenic zones; 2 – sources located beyond seismogenic zones; 3 – estimates of seismic potential Мmax, parameter b and seismic activity reduced to magnitude M=4.0.
Оценки величины максимального возможного землетрясения сейсмогенных зон были получены на основе сейсмологических и сейсмотектонических методов определения величины Мmax, детально описанных в работах [Ibragimov et al., 2002; Artikov et al., 2020a]. Расчет сейсмической опасности проводился при наибольшем значении величины Мmax в сейсмогенной зоне при сейсмологическом и сейсмотектоническом его определении. Для сейсмических источников, расположенных вне сейсмогенных зон, величина сейсмического потенциала получалась путем добавления к магнитуде максимального наблюденного землетрясения в этом источнике половины магнитудной единицы.
Определение параметров повторяемости для модели источников в виде сейсмогенных зон проводилось следующим образом. Для источников, в пределы которых попадало достаточное количество сейсмических событий для надежного построения графика повторяемости, сейсмическая активность, отнесенная к магнитуде M=4.0, и угловой коэффициент прямой (параметр b) снимались непосредственно с этого графика. Для сейсмогенерирующих зон с малым числом сейсмических событий принималось региональное значение параметра b, а сейсмическая активность при данном значении угла наклона графика повторяемости рассчитывалась по выборке землетрясений, попадающих непосредственно в пределы сейсмического источника. При этом использовались традиционные методы распределения и суммирования [Gorbunova, 1964; Riznichenko, 1985] определения сейсмической активности. Значения сейсмического потенциала и параметров повторяемости землетрясений для каждого сейсмического источника в модели сейсмогенных зон приведены на рис. 7.
4.3. Модель площадных источников
Контуры модели площадных источников были сформированы нами при разработке карт общего сейсмического районирования территории Узбекистана ОСР-2017 [Artikov et al., 2020a]. В целом, данная модель достаточно отчетливо отражает блоковое строение земной коры и особенности распределения сейсмичности в пределах орогенической и платформенной части исследуемой территории, разграниченных Западно-Тянь-Шаньским линеаментом. В Восточном Узбекистане были выделены три мегазоны: Приташкентская, Таласо-Ферганская, Ферганская впадина и ее горное обрамление. В Южном Узбекистане авторы рассматривали Южно-Узбекистанскую мегазону, включающую юго-западные отроги Гисcара. На территории Западного Узбекистана выделены Западная и Северо-Западная мегазоны. Отдельно, ввиду особых сейсмологических условий, рассматривался район Газли. В свою очередь, сами мегазоны также были поделены на подзоны – участки с различной сейсмической активностью. Для адекватной оценки сейсмической опасности приграничных районов в рассмотрение были включены дополнительные площадные зоны, расположенные частично или полностью на территории соседних государств.
В качестве оценки сейсмического потенциала площадных источников использовалось значение, полученное добавлением к магнитуде максимального наблюденного землетрясения в этом источнике 0.3–0.5М магнитудных единиц. Правило нахождения параметров повторяемости для модели источников в виде площадных зон было такое же, как и для модели сейсмогенных зон. Конфигурация модели площадных источников с указанием их сейсмического потенциала и параметров повторяемости приведена на рис. 8.
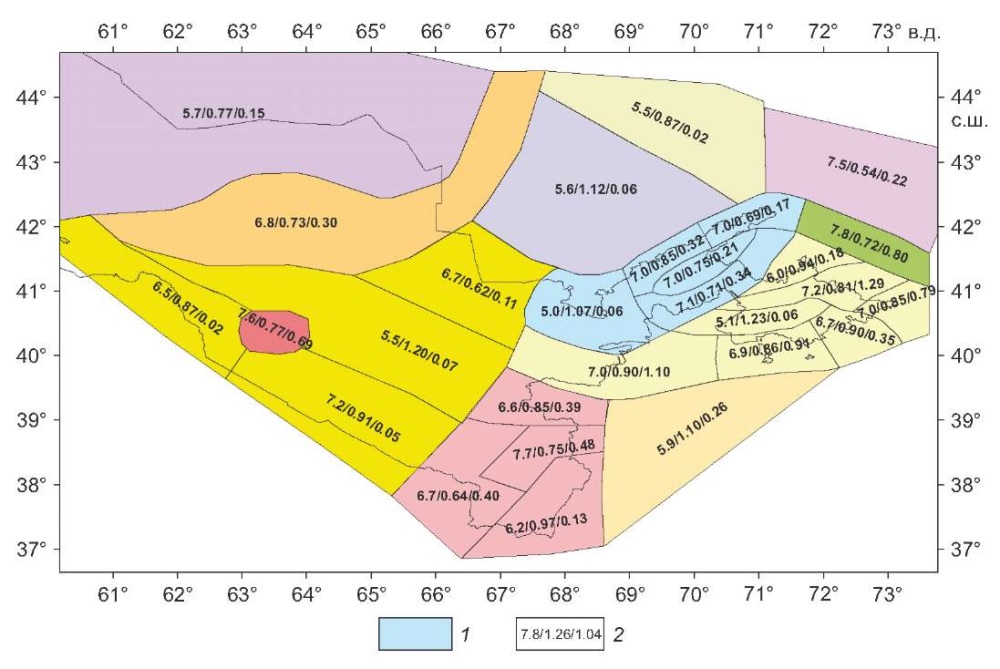
Рис. 8. Модель площадных источников. 1 – контуры источника; 2 – оценки сейсмического потенциала Мmax, параметра b и сейсмической активности, приведенной к магнитуде М=4.0.
Fig. 8. Model of area sources. 1 – source contours; 2 – estimates of seismic potential Мmax, b-value parameter and seismic activity reduced to magnitude M=4.0.
5. КАРТЫ СЕЙСМИЧЕСКОЙ ОПАСНОСТИ ТЕРРИТОРИИ УЗБЕКИСТАНА В ПОКАЗАТЕЛЯХ МАКРОСЕЙСМИЧЕСКОЙ ИНТЕНСИВНОСТИ
Расчеты сейсмической опасности проводились программным комплексом CRISIS [Ordaz et al., 2007], который широко используется в мире для вероятностного анализа сейсмической опасности. Шаг сетки, по которой производился расчет, составлял 0.2×0.2°.
Учет эпистемических неопределенностей в выборе сейсмических источников проводился путем построения логического дерева. При этом каждой из рассмотренных моделей был придан определенный вес (w):
- модель площадных источников – w=1/3;
- модель сейсмогенных зон – w=1/3;
- модель активных разломов с классом достоверности А и В – w=1/12;
- модель активных разломов с классом достоверности А, В и С – w=1/6;
- модель активных разломов с классом достоверности А, В, С и D – w=1/12.
Таким образом, суммарный вес всех пяти моделей сейсмических источников равнялся wΣ=1. При этом общий вес моделей активных разломов земной коры с различной группой достоверности составил wfault=1/3, т.е. являлся таким же, как и для моделей площадных источников и сейсмогенных зон. Центральной модели активных разломов (с классом достоверности А, В и С) был придан больший вес, нежели двум другим, как в меру консервативной.
На рис. 9 приведены карты сейсмического районирования территории Узбекистана в баллах макросейсмической шкалы для вероятностей Р=0.90 и Р=0.98 непревышения уровня сейсмических воздействий в течение 50 лет. Поскольку законы затухания интенсивности сейсмических воздействий с расстоянием разрабатываются для средних грунтовых условий, каковыми для территории Узбекистана являются грунты II категории по сейсмическим свойствам, построенные карты относятся именно к этой грунтовой категории.
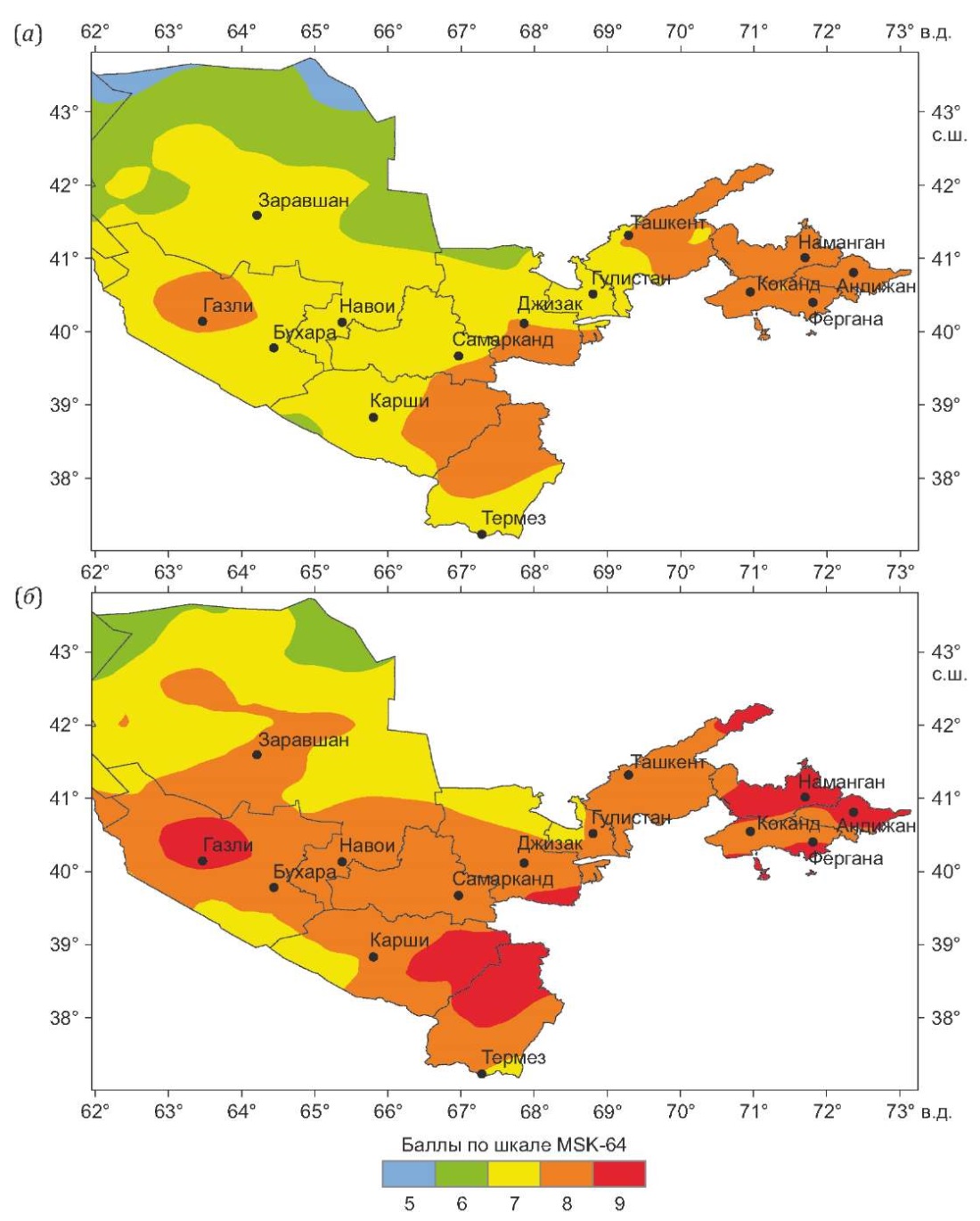
Рис. 9. Карта сейсмического районирования территории Узбекистана в баллах макросейсмической шкалы MSK-64 для различных вероятностей Р непревышения уровня сейсмических воздействий в течение 50 лет. (а) – Р=0.90; (б) – Р=0.98.
Fig. 9. A seismic zoning map of Uzbekistan in points of the MSK-64 scale for different probabilities P of occurrence of non-exceedance level earthquakes in the next 50 years. (a) – P=0.90; (б) – P=0.98.
На рис. 10 показаны кривые опасности для некоторых крупных городов Узбекистана. По оси абсцисс отложена величина сейсмического воздействия в баллах MSK-64, а по оси ординат – вероятность его превышения в течение 50 лет. Горизонтальными линиями на рисунке показаны периоды повторения сейсмических воздействий, отвечающие различным вероятностям превышения уровня воздействий.
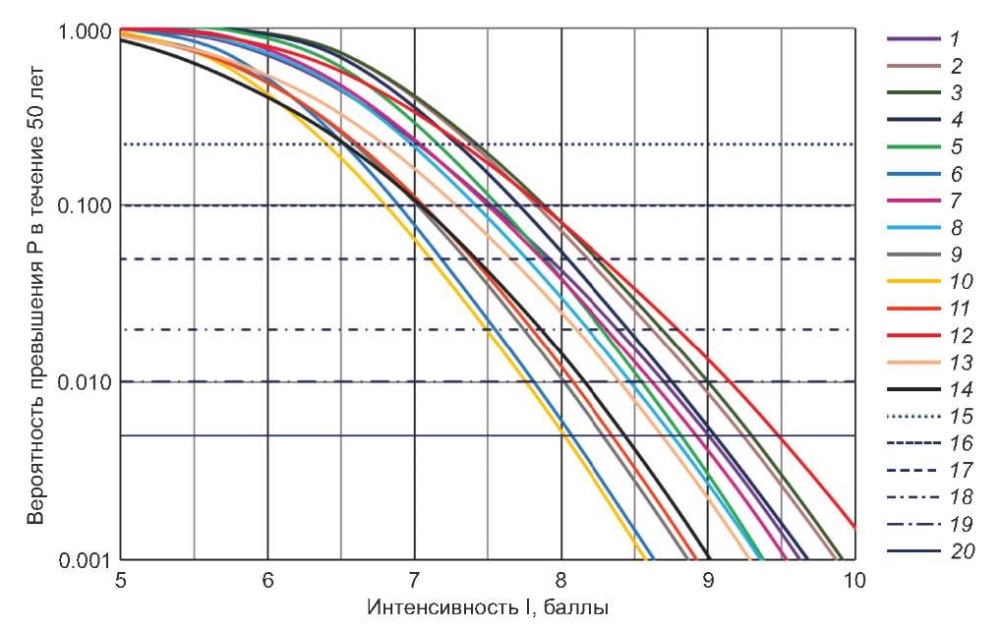
Рис. 10. Кривые опасности некоторых крупных городов Узбекистана.
1–14 –кривые опасности городов: 1 – Ташкент, 2 – Андижан, 3 – Наманган, 4 – Фергана, 5 – Коканд, 6 – Гулистан, 7 – Джизак, 8 – Самарканд, 9 – Карши, 10 – Термез, 11 – Бухара, 12 – Газли, 13 – Навои, 14 – 3арафшан; 15–20 – линии, отвечающие различным периодам (Т) повторения сотрясений: 15 – Т=200 лет, 16 – Т=475 лет, 17 – Т=975 лет, 18 – Т=2475 лет, 19 – Т=4975 лет, 20 – Т=9975 лет.
Fig. 10. Hazard curves of some major cities in Uzbekistan.
1–14 – hazard curves of: 1 – Tashkent, 2 – Andijan, 3 – Namangan, 4 – Fergana, 5 – Kokand, 6 – Gulistan, 7 – Jizzakh, 8 – Samarkand, 9 – Karshi, 10 – Termez, 11 – Bukhara, 12 – Gazli, 13 – Navoi, 14 – Zarafshan; 15–20 – lines corresponding to different earthquake recurrence periods (T): 15 – T=200 years, 16 – T=475 years, 17 – T=975 years, 18 – T=2475 years, 19 – T=4975 years, 20 – T=9975 years.
6. ЗАКЛЮЧЕНИЕ
На основе выполненных исследований проведено ранжирование законов затухания интенсивности сейсмических воздействий с расстоянием, разработанных для Центрально-Азиатского региона, двумя различными методами (LH и LLH). В результате проведенной процедуры ранжирования построена обобщенная модель затухания интенсивности сейсмических воздействий с расстоянием для землетрясений различного энергетического уровня.
Для оценки сейсмической опасности территории Узбекистана рассмотрено пять альтернативных моделей сейсмических источников: модель площадных источников, модель сейсмогенных зон и три модели активных разломов земной коры с различной степенью достоверности проявления современной геодинамической активности в новейший и современный период времени. Проведена сейсмологическая параметризация построенных моделей сейсмических источников, включающая определение сейсмического потенциала, параметров повторяемости землетрясений различных магнитуд, преобладающего кинематического типа подвижки в очагах для каждого источника.
С использованием построенных моделей сейсмических источников и модели сейсмического эффекта получены вероятностные характеристики сейсмической опасности в значениях макросейсмической интенсивности для территории Узбекистана. Для различных вероятностей непревышения уровня сейсмических воздействий в течение 50 лет составлены карты сейсмического районирования. Для ряда крупных городов республики построены кривые опасности.
7. ЗАЯВЛЕННЫЙ ВКЛАД АВТОРОВ / CONTRIBUTION OF THE AUTHORS
Все авторы внесли эквивалентный вклад в подготовку рукописи, прочли и одобрили финальную версию перед публикацией.
All authors made an equivalent contribution to this article, read and approved the final manuscript.
8. РАСКРЫТИЕ ИНФОРМАЦИИ / DISCLOSURE
Авторы заявляют об отсутствии конфликта интересов, связанного с этой рукописью.
The authors declare that they have no conflicts of interest relevant to this manuscript.
Список литературы
1. Anderson J.G., Luco J.E., 1983. Consequences of Slip Rate Constants on Earthquake Occurrence Relations. Bulletin of the Seismological Society of America 73 (2), 471–496. DOI:10.1785/BSSA0730020471.
2. Artikov T.U., Ibragimov R.S., Ibragimova T.L., Mirzaev M.A., 2016. Study of Modern Seismic Zoning Maps’ Accuracy (Case for Eastern Uzbekistan). Geodesy and Geodynamics 7 (6), 416–424. https://doi.org/10.1016/j.geog.2016.04.015.
3. Artikov T.U., Ibragimov R.S., Ibragimova T.L., Mirzaev M.A., 2018. Methodology of Developing the New Complex of General Seismic Zoning Maps of Uzbekistan Territory OSR-2017. Georisk 12 (2), 6–24 (in Russian) [Артиков Т.У., Ибрагимов Р.С., Ибрагимова Т.Л., Мирзаев М.А. Методология построения нового комплекса карт общего сейсмического районирования территории Узбекистана ОСР-2017 // Геориск. 2018. Т. 12. № 2. С. 6–24].
4. Artikov T.U., Ibragimov R.S., Ibragimova T.L., Mirzaev M.A., 2020a. Complex of General Seismic Zoning Maps OSR-2017 of Uzbekistan. Geodesy and Geodynamics 11 (4), 273–292. https://doi.org/10.1016/j.geog.2020.03.004.
5. Artikov T.U., Ibragimov R.S., Ibragimova T.L., Mirzaev M.A., 2020b. Models of the Macroseismic Field Earthquakes and Their Influence on Seismic Hazard Assessment Values for Central Asia. Geodynamics & Tectonophysics 11 (3), 606–623 (in Russian) [Артиков Т.У., Ибрагимов Р.С., Ибрагимова Т.Л., Мирзаев М.A. Модели макросейсмического поля землетрясений Центральной Азии и их влияние на результирующие оценки сейсмической опасности // Геодинамика и тектонофизика. 2020. Т. 11. № 3. С. 606–623]. https://doi.org/10.5800/GT-2020-11-3-0494.
6. Bindi D., Parolai S., Oth A., Abdrahmatov K., Muraliev A., Zschau J., 2011. Intensity Prediction Equations for Central Asia. Geophysical Journal International 187 (1), 327–337. https://doi.org/10.1111/j.1365-246X.2011.05142.x.
7. Bungum H., 2007. Numerical Modelling of Fault Activities. Computers & Geophysics 33 (6), 808–820. https://doi.org/10.1016/j.cageo.2006.10.011.
8. Bykova V.V., Tatevosyan R.E., 2015. Basic Principles of Probabilistic of Seismic Hazard Analysis by the Example of the Main Gas Pipeline Section. In: Problems of Integrated Geophysical Monitoring in the Russian Far East. Proceedings of the Fifth Scientific and Technical Conference (September 27 – October 3, 2015). KB FRC GS RAS, Petropavlovsk-Kamchatsky, p. 134–138 (in Russian) [Быкова В.В., Татевосян Р.Э. Об основных принципах вероятностного анализа сейсмической опасности на примере участка магистрального газопровода // Проблемы комплексного геофизического мониторинга Дальнего Востока России: Труды Пятой научно-технической конференции (27 сентября – 3 октября 2015 г.). Петропавловск-Камчатский: КФ ФИЦ ЕГС РАН, 2015. С. 134–138].
9. Chernov Yu.K., 1989. Strong Ground Motions and Quantitative Assessment of Seismic Hazard for the Areas. Fan, Tashkent, 296 p. (in Russian) [Чернов Ю.К. Сильные движения грунта и количественная оценка сейсмической опасности территорий. Ташкент: Фан, 1989. 296 с.].
10. Cornell C.A., 1968. Engineering Seismic Risk Analysis. Bulletin of the Seismological Society of America 58 (5), 1583–1606. https://doi.org/10.1785/BSSA0580051583.
11. Gorbunova I.V., 1964. Constant Accuracy in Mapping. In: Experimental Seismics. Publishing House of the USSR Academy of Sciences, Moscow, p. 138–147 (in Russian) [Горбунова И.В. Построение карт активности с постоянной точностью // Экспериментальная сейсмика. М.: Изд-во АН СССР, 1964. С. 138–147].
12. Hanks T.C., Bakun W.H., 2008. M-logA Observations for Recent Large Earthquakes. Bulletin of the Seismological Society of America 98 (1), 490–494. https://doi.org/10.1785/0120070174.
13. Ibragimov R.N., Nurmatov U.O., Ibragimov O.R., 2002. Seismotectonic Method for Assessing Seismic Hazard and Issues of Seismic Zoning. In: Seismic Zoning and Earthquake Forecasting in Uzbekistan. Hydroingeo, Tashkent, p. 59–74 (in Russian) [Ибрагимов Р.Н., Нурматов У.О., Ибрагимов О.Р. Сейсмотектонический метод оценки сейсмической опасности и вопросы сейсмического районирования // Сейсмическое районирование и прогноз землетрясений в Узбекистане. Ташкент: Гидроингео, 2002. С. 59–74].
14. Ibragimov R.S., Ibragimova T.L., Mirzaev M.A., Ashurov S.H., 2022a. Comparison of Seismic Hazard Assessments Obtained with the Probabilistic and Probabilistic-Deterministic Approaches for the Territory of Uzbekistan. Seismic Instruments 58, S14–S24. https://doi.org/10.3103/S0747923922070040.
15. Ibragimov R.S., Ibragimova T.L., Mirzaev M.A., Ashurov S.H., 2022b. Comparison of Seismic Hazard Assessments Obtained within the Probabilistic and Probabilistic-Deterministic Approaches for the Territory of Uzbekistan. Questions of Engineering Seismology 49 (4), 21–35 (in Russian) [Ибрагимов Р.С., Ибрагимова Т.Л., Мирзаев М.А., Ашуров С.Х. Сопоставление оценок сейсмической опасности, получаемых в рамках вероятностного и вероятностно-детерминистического подходов, для территории Узбекистана // Вопросы инженерной сейсмологии. 2022. Т. 49. № 4. С. 21–35]. https://doi.org/10.21455/VIS2022.4-2.
16. Ibragimova T.L., Ibragimov R.S., Mirzaev M.A., Rebetsky Yu.L., 2021. The Current Stress of Earth’s Crust in the Territory of Uzbekistan According to Focal Earthquake Mechanisms. Geodynamics & Tectonophysics 12 (3), 435–454 (in Russian) [Ибрагимова Т.Л., Ибрагимов Р.С., Мирзаев М.А., Ребецкий Ю.Л. Современное напряженное состояние земной коры территории Узбекистана по данным сборного каталога механизмов очагов землетрясений // Геодинамика и тектонофизика. 2021. Т. 12. № 3. С. 435–454]. https://doi.org/10.5800/GT-2021-12-3-0532.
17. Kovesligethy R., 1907. Seismischer Starkegral und Intensität der Beben. Gerlands Beiträge zur Geophysik 8, 22–29.
18. Leonard M., 2010. Earthquake Fault Scaling: Self-Consistent Relating of Rupture Length, Width, Average Displacement, and Moment Release. Bulletin of the Seismological Society of America 100 (5A), 1971–1988. https://doi.org/10.1785/0120090189.
19. Leonard M., 2014. Self-Consistent Earthquake Fault-Scaling Relations: Update and Extension to Stable Continental Strike-Slip Faults. Bulletin of the Seismological Society of America 104 (6), 2953–2965. https://doi.org/10.1785/0120140087.
20. McGuire R.K., 2004. Seismic Hazard and Risk Analysis. Earthquake Engineering Research Institute, Oakland, California, 240 p.
21. Nowroozi A.А., 1985. Empirical Relations between Magnitude and Fault Parameters for Earthquake in Iran. Bulletin of Seismological Society of America 75 (5), 1327–1338. DOI:10.1785/BSSA0750051327.
22. Ordaz M., Aguilar A., Arboleda J., 2007. CRISIS2007. Program for Computing Seismic Hazard. Available from: https://ecapra.org/topics/crisis-2007 (Last Accessed March 31, 2016).
23. Rebetsky Yu.L., Ibragimova T.L., Ibragimov R.S., Mirzaev M.A., 2020. Stress State of Uzbekistan’s Seismically Active Areas. Seismic Instruments 56, 679–700, https://doi.org/10.3103/S0747923920060079.
24. Riznichenko Yu.V., 1985. Problems of Seismology. Nauka, Moscow, 408 p. (in Russian) [Ризниченко Ю.В. Проблемы сейсмологии. М.: Наука, 1985. 408 с.].
25. Riznichenko Yu.V., Seiduzova S.S., 1984. Spectral-Temporal Characteristics of Seismic Hazard. Nauka, Moscow, 182 p. (in Russian) [Ризниченко Ю.В., Сейдузова С.С. Спектрально-временная характеристика сейсмической опасности. М.: Наука, 1984. 182 с.].
26. Scherbaum F., Cotton F., Smit P., 2004. On the Use of Response Spectral-Reference Data for the Selection of Ground-Motion Models for Seismic Hazard Analysis: The Case of Rock Motion. Bulletin of the Seismological Society of America 94 (6), 2164–2185. https://doi.org/10.1785/0120030147.
27. Scherbaum F., Delavaud E., Riggelsen C., 2009. Model Selection in Seismic Hazard Analysis: An Information-Theoretic Perspective. Bulletin of the Seismological Society of America 99, 3234–3247. https://doi.org/10.1785/0120080347.
28. Shebalin N.V., 1968. Methods to Use Engineering and Seismological Data for Seismic Zoning. In: Seismic Zoning of the USSR. Nauka, Moscow, p. 95–111 (in Russian) [Шебалин Н.В. Методы использования инженерно-сейсмологических данных при сейсмическом районировании // Сейсмическое районирование СССР. М.: Наука, 1968. С. 95–111].
29. Shebalin N.V., 1972. Macroseismic Data as Information on Source Parameters of Large Earthquakes. Physics of the Earth and Planetary Interiors 6 (4), 316–323. https://doi.org/10.1016/0031-9201(72)90016-7.
30. Shteinberg V.V., Ponomareva O.N., 1987. Large Earthquake Source Dimensions. Problems of Engineering Seismology 28, 63–72 (in Russian) [Штейнберг В.В., Пономарева О.Н. О размерах очагов сильных землетрясений // Вопросы инженерной сейсмологии. 1987. Вып. 28. C. 63–72].
31. Wells D.L., Coppersmith K.J., 1994. New Empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area and Surface Displacement. Bulletin of the Seismological Society of America 84 (4), 974–1002. https://doi.org/10.1785/BSSA0840040974.
32. Youngs R.R., Coppersmith K.J., 1985. Implications of Fault Slip Rates and Earthquake Recurrence Models to Probabilistic Seismic Hazard Estimates. Bulletin of the Seismological Society of America 75 (4), 939–964. DOI:10.1785/BSSA0750040939.
33. Zelenin E., Bachmanov D., Garipova S., Trifonov V., Kozhurin A., 2022. The Active Faults of Eurasia Database (AFEAD): The Ontology and Design behind the Continental-Scale Dataset. Earth System Science Data 14 (10), 4489–4503. https://doi.org/10.5194/essd-14-4489-2022.
Об авторах
Р. С. ИбрагимовУзбекистан
100128, Ташкент, ул. Зульфияхонима, 3
Т. Л. Ибрагимова
Узбекистан
100128, Ташкент, ул. Зульфияхонима, 3
М. А. Мирзаев
Узбекистан
100128, Ташкент, ул. Зульфияхонима, 3
С. Х. Ашуров
Узбекистан
100128, Ташкент, ул. Зульфияхонима, 3
Рецензия
Для цитирования:
Ибрагимов Р.С., Ибрагимова Т.Л., Мирзаев М.А., Ашуров С.Х. РАНЖИРОВАНИЕ ЗАКОНОВ ЗАТУХАНИЯ ИНТЕНСИВНОСТИ СЕЙСМИЧЕСКИХ ВОЗДЕЙСТВИЙ И ПОСТРОЕНИЕ МОДЕЛЕЙ СЕЙСМИЧЕСКИХ ИСТОЧНИКОВ ПРИ ОЦЕНКЕ СЕЙСМИЧЕСКОЙ ОПАСНОСТИ ТЕРРИТОРИИ УЗБЕКИСТАНА. Геодинамика и тектонофизика. 2024;15(4):0770. https://doi.org/10.5800/GT-2024-15-4-0770. EDN: PEIYOD
For citation:
Ibragimov R.S., Ibragimova T.L., Mirzaev M.A., Ashurov S.H. RANKING OF SEISMIC INTENSITY ATTENUATION LAWS AND MODELING OF SEISMIC SOURCES FOR SEISMIC HAZARD ASSESSMENT IN UZBEKISTAN. Geodynamics & Tectonophysics. 2024;15(4):0770. https://doi.org/10.5800/GT-2024-15-4-0770. EDN: PEIYOD



















































