Перейти к:
ОСОБЕННОСТИ ПОЛУЧЕНИЯ ГЕОЭЛЕКТРИЧЕСКИХ ХАРАКТЕРИСТИК СРЕДЫ В ЭКСПЕРИМЕНТАЛЬНОМ ЭЛЕКТРОРАЗВЕДОЧНОМ КОМПЛЕКСЕ С ШУМОПОДОБНЫМИ СИГНАЛАМИ
https://doi.org/10.5800/GT-2025-16-2-0820
EDN: NUFKJW
Аннотация
Рассматривается методика получения геоэлектрических характеристик среды для экспериментального электроразведочного комплекса с шумоподобными сигналами, предназначенного для изучения современных геодинамических процессов, происходящих в литосфере Северного Тянь-Шаня, с учетом особенностей его аппаратурно-программной реализации. Рассмотрено влияние нестабильности амплитуды зондирующих импульсов тока на кривую становления поля при питании зондирующей установки от аккумуляторных батарей. Предлагается методика учета изменения тока в зондирующей рамке, позволившая дополнительно улучшить соотношение сигнал – помеха в получаемых кривых зондирования. На основе работ В.А. Сидорова и М.С. Жданова показаны варианты приближенного решения обратной задачи методом зондирования становлением поля в ближней зоне (ЗСБ), реализованные в программном обеспечении электроразведочного комплекса. Рассмотрен способ улучшения метода решения обратной задачи ЗСБ в рамках модели с проводящей S плоскостью, позволяющий повысить достоверность получаемых результатов.
Ключевые слова
Для цитирования:
Бобровский В.В., Ильичев П.В. ОСОБЕННОСТИ ПОЛУЧЕНИЯ ГЕОЭЛЕКТРИЧЕСКИХ ХАРАКТЕРИСТИК СРЕДЫ В ЭКСПЕРИМЕНТАЛЬНОМ ЭЛЕКТРОРАЗВЕДОЧНОМ КОМПЛЕКСЕ С ШУМОПОДОБНЫМИ СИГНАЛАМИ. Геодинамика и тектонофизика. 2025;16(2):0820. https://doi.org/10.5800/GT-2025-16-2-0820. EDN: NUFKJW
For citation:
Bobrovsky V.V., Ilyichev P.V. FEATURES OF OBTAINING GEOELECTRIC CHARACTERISTICS OF THE ENVIRONMENT IN AN EXPERIMENTAL ELECTRICAL PROSPECTING COMPLEX WITH PSEUDONOISE SIGNALS. Geodynamics & Tectonophysics. 2025;16(2):0820. (In Russ.) https://doi.org/10.5800/GT-2025-16-2-0820. EDN: NUFKJW
1. ВВЕДЕНИЕ
Одним из главных достоинств метода становления поля при изучении современных геодинамических процессов в земной коре является его высокая чувствительность к изменениям геоэлектрического разреза [Svetov, 1992]. На Научной станции Российской академии наук в г. Бишкеке (НС РАН) уже больше 30 лет непрерывно действует система электромагнитного мониторинга земной коры, осуществляемая методом становления поля в дальней зоне (ЗСД) [Bobrovsky et al., 2023b]. Одним из главных направлений развития этой системы является расширение ее возможностей за счет использования других методов активной электроразведки.
Для более детального изучения изменений электрических свойств геологического разреза для территории Северного Тянь-Шаня в НС РАН проводятся исследования, направленные на создание экспериментального электроразведочного измерительного комплекса, в основу которого положен метод зондирования становлением поля в ближней зоне (ЗСБ). Для повышения точности измерения электрических параметров земной коры (кажущееся сопротивление) появилась идея применения для электромагнитного зондирования земной коры шумоподобных зондирующих сигналов, обладающих уникальными статистическими свойствами, и в первую очередь так называемой большой «информационной избыточностью» [Gantmakher at al., 2005; Zepernick, Finger, 2005; Varakin, 1985]. Применению шумоподобных сигналов (ШПС) в активной электроразведке посвящен ряд работ зарубежных [Duncan at al., 1980] и отечественных [Svetov et al., 2012; Ilyichev, Bobrovsky, 2015; Velikin A.B., Velikin A.A., 2016; Goncharov et al., 2022] авторов. Применение ШПС с последующей корреляционной обработкой регистрируемых сигналов позволяет получить значительное преимущество в соотношении сигнал – шум по сравнению с традиционными системами, использующими для зондирования биполярные импульсные последовательности с постоянной длительностью импульсов [Ilyichev, Bobrovsky, 2015].
Основной задачей разрабатываемой аппаратуры является ее использование в системе активного электромагнитного мониторинга геодинамических процессов в сейсмоактивных зонах Северного Тянь-Шаня. Ввиду локальности и детальности метода ЗСБ особый интерес представляет его применение при проведении комплексных полевых экспериментов (совместно с системой сейсмического и магнитного мониторинга) в области активных разломов с целью исследования необратимых процессов в области разрушения горной породы с учетом влияния лунно-солнечных приливов и магнитных аномалий. Такое применение накладывает повышенные требования к стабильности и чувствительности измерительной аппаратуры, используемой при проведении исследований. Данная статья продолжает тематику, начатую в работе [Bobrovsky et al., 2023a] и освещающую особенности получения геоэлектрических характеристик среды для экспериментального электроразведочного комплекса с шумоподобными сигналами (ЭРК ШПС) [Bobrovsky et al., 2021] с учетом особенностей его аппаратурно-программной реализации.
В данной работе рассмотрена методика обработки сигналов, регистрируемых ЭРК ШПС в сеансах зондирования земной коры с учетом изменения тока в зондирующей рамке, позволяющая улучшить соотношение сигнал – помеха в получаемых кривых зондирования. Результаты применения данной методики позволят улучшить качество и стабильность временных рядов кажущегося сопротивления, использующегося в качестве основного параметра для электромагнитных исследований современных геодинамических процессов в литосфере Северного Тянь-Шаня.
На основании анализа решения прямой задачи ЗСБ [Sidorov, 1985] подробно описан способ улучшения метода решения обратной задачи ЗСБ в рамках модели с проводящей S плоскостью.
2. МЕТОДЫ И МАТЕРИАЛЫ
Все результаты, приведенные в данной работе, получены в процессе отработки экспериментального измерительного комплекса ЭРК ШПС. Детальные характеристики аппаратуры и описание программного обеспечения ЭРК ШПС приведены в работе [Bobrovsky et al., 2021]. В качестве источников силового питания генераторных устройств в активной электроразведке могут применяться аккумуляторные батареи постоянного напряжения, бензогенераторы и другие источники одно- или трехфазного переменного тока частотой 50 Гц. В ЭРК ШПС в качестве источника силового питания используется аккумуляторная батарея напряжением 200 В, составленная из 18 автомобильных аккумуляторов емкостью 60 А·ч. Такой выбор обусловлен тем, что бензогенераторы являются источником сильных помех, которые находятся в полосе пропускания измерительного канала. Поскольку, в отличие от классического режима работы, в методе ЗСБ с применением шумоподобных сигналов измерения проводятся не в режиме снятия тока, а в режиме его переключения, необходимо обеспечить не только стабильность значения тока, но и стабильность его формы. Так как аккумуляторные батареи не являются идеальным источником тока, в момент нагрузки, под воздействием электрохимических процессов, амплитуда тока меняется сложным образом, что приводит к искажению кривой становления поля при дальнейшей корреляционной обработке. Разработка стабилизатора тока для таких систем представляет собой довольно сложную задачу, поскольку, в отличие от классических систем, где необходимо обеспечить стабильность тока к концу импульса, в системах с ШПС необходимо обеспечить стабильность тока как минимум с момента окончания фронта его нарастания. Авторами предложено решение, основанное на регистрации модуля тока в зондирующей рамке на протяжении всего измерительного сеанса и вычислении специальной нормировочной функции, для учета нестабильности амплитуды зондирующих импульсов тока в регистрируемых сигналах становления поля.
Основным контролируемым параметром при изучении современных геодинамических процессов в литосфере, получаемым в результате обработки, является график изменения кажущегося удельного электрического сопротивления ρτ(t) во времени. Однако при выполнении мониторинга необходимо иметь хотя бы приблизительное представление о свойствах геоэлектрического разреза в точке проведения измерений. Обычно для различных методов электромагнитного зондирования интерпретация полевых измерений осуществляется методом подбора, который основан на минимизации функционала, описывающего расхождение измеренной и теоретической кривой становления поля. Как правило, берутся теоретические кривые, рассчитанные для модели горизонтально-слоистой среды. Подобная интерпретация данных требует определенной квалификации исследователя и значительной вычислительной мощности, что делает ее малоэффективной в полевых условиях. Непосредственные результаты полевых измерений не отражают особенности геоэлектрического разреза. «В ближней зоне источника и при импульсном возбуждении поля форма кривых связана с особенностями разреза наиболее сложным образом» [Tikshaev, 1984, с. 142]. Для качественной (а иногда и количественной) оценки геоэлектрического разреза в геоэлектроразведке применяются различные трансформации измеренных кривых, которые легко осуществить в полевых условиях. В данной статье рассмотрим методику расчета кажущейся продольной проводимости Sτ и глубины погружения пленки hτ в рамках модели проводящей горизонтальной плоскости в непроводящей среде [Tikshaev, 1984; Sidorov, 1985] применительно к ЭРК ШПС. Данные параметры необходимы для дальнейшей реализации в программном обеспечении ЭРК ШПС трансформации, предложенной В.А. Сидоровым и В.В. Тикшаевым. Трансформация заключается в расчете и построении кривой кажущейся продольной проводимости разреза Sτ(hτ).
3. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ОБСУЖДЕНИЕ
3.1. Учет нестабильности амплитуды зондирующих импульсов тока при расчете кривой становления поля в системах с шумоподобными сигналами
В отличие от традиционных способов зондирования становлением поля, в ЭРК ШПС используются шумоподобные зондирующие сигналы. В этом случае корреляционная обработка регистрируемых на приемной стороне сигналов на фоне значительных шумов и помех различного происхождения, обеспечивает многократное повышение соотношения сигнал – шум. Отличием предлагаемого метода зондирования от типового является то, что при применении шумоподобных зондирующих сигналов с широким спектром и измерении ЭДС – e(t) в приемной рамке, как в традиционном методе, после корреляционной обработки зарегистрированных сигналов мы будем получать сигнал, пропорциональный скорости изменения ЭДС или второй производной от магнитного потока Ф"(t)=e'(t), так как корреляционная обработка шумоподобных сигналов с широким спектром приводит к дифференцированию сигнала, поэтому в ЭРК ШПС используется датчик интегрирующего типа, который обеспечивает на своем выходе сигнал, пропорциональный магнитному потоку Ф(t) [Bobrovsky et al., 2023a]. В этом случае дальнейшая корреляционная обработка регистрируемого на приемной стороне сигнала позволяет получить кривую, которая со времени, равного длительности минимального импульса зондирующей M-последовательности (МП), будет приближаться к ЭДС. Корреляционная обработка заключается в вычислении взаимной корреляционной функции (ВКФ) между одиночной идеальной М-последовательностью единичной амплитуды с параметрами (кроме амплитуды), аналогичными параметрам реальной зондирующей последовательности, и регистрируемым откликом среды на зондирующее воздействие S(t) (рис. 1).
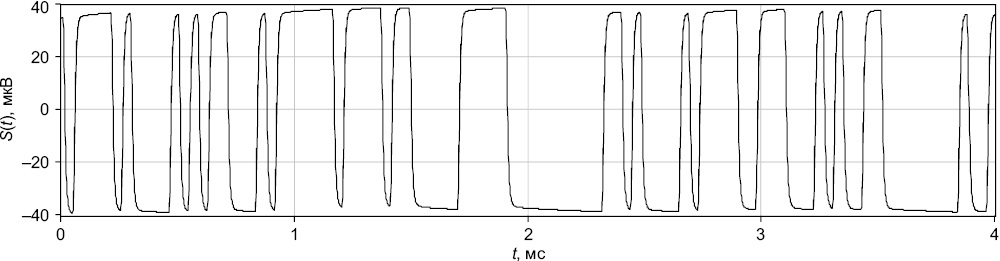
Рис. 1. Фрагмент зарегистрированного сигнала отклика среды на зондирующее воздействие.
Fig. 1. A fragment of the recorded signal of the environment’s response to the probing effect.
После корреляционной обработки выполняется дальнейшее накопление периодических сигналов ВКФ за исключением сигналов от первой и последней МП, что обеспечивает дополнительное улучшение соотношения сигнал – шум. Фактически к достоинствам обычного накопления детерминированных сигналов добавляются существенные преимущества, получаемые за счет применения корреляционной обработки ШПС. Подробно весь процесс корреляционной обработки описан в работе [Ilyichev, Bobrovsky, 2015].
Второй отличительной особенностью применения ШПС в электроразведке является необходимость работы измерительной системы в режиме переключения тока, поскольку любое нарушение последовательности зондирующих импульсов (к примеру введение пауз) приводит к значительным искажениям кривой становления поля, получаемой в результате корреляционной обработки регистрируемых сигналов. В свою очередь, такой режим работы предполагает повышенные требования к стабильности амплитуды и формы зондирующего тока.
Для обеспечения контроля амплитуды импульсов тока в индукционной зондирующей рамке в состав ЭРК ШПС был введен датчик измерения модуля тока. Для исследования поведения аккумуляторной батареи в процессе проведения измерительных сеансов использовались данные, полученные при проведении серии полевых экспериментов по зондированию земной коры в двух точках на местности («МГД» и «Чункурчак»). В каждой точке на местности было проведено одиннадцать сеансов зондирования земной коры. Зондирование выполнялось квадратной зондирующей рамкой размером 50×50 м при амплитуде импульсов тока 8 А. Основные параметры регистрации приведены в табл. 1.
Таблица 1. Основные параметры регистрации сигналов отклика среды
Table 1. Basic parameters for recording environmental response signals
Тип зондирующей последовательности | Длительность одиночной МП, с | Количество МП в изм. сеансе | Частота дискретизации, кГц | Суммарный коэффициент усиления изм. канала |
Биполярная бинарная МП | 6.57 | 41 | 224.438 | 18764.43 |
Для контроля стабильности параметров измерительного канала в начале каждой измерительной сессии перед тремя первыми сеансами и в конце всей сессии проводились градуировки измерительного канала с индукционным датчиком. В сеансах зондирования земной коры синхронно регистрировались сигналы измерительного канала приемного индукционного датчика и канала измерения модуля тока в зондирующей рамке. Для построения графиков изменения тока во время каждого сеанса зондирования регистрируемые каналом измерения тока сигналы подвергались предварительной обработке с помощью медианного фильтра Дирихле первого порядка [Gutnikov, 1990], с окном, длительность которого была выбрана равной длительности одиночной шумоподобной МП. Предполагалось, что это обеспечит практически полное подавление в зарегистрированных сигналах всех спектральных составляющих зондирующих импульсов, т.е. должна была получиться огибающая зарегистрированных сигналов. В спектре получаемых при этом сигналов оставались составляющие с частотой, кратной примерно 1 Гц. Для удаления оставшихся помех после фильтра Дирихле первого порядка с длительностью окна, равной 6.57 с, был дополнительно применен еще один фильтр Дирихле третьего порядка с окном, длительность которого определялась частотой оставшихся тональных помех (≈1.0 с). В результате такой обработки вычислялась огибающая зондирующих импульсов тока I(t). На рис. 2 приведены графики огибающей зондирующих импульсов тока для одного полевого эксперимента, выполнявшегося на измерительной точке «Чункурчак».
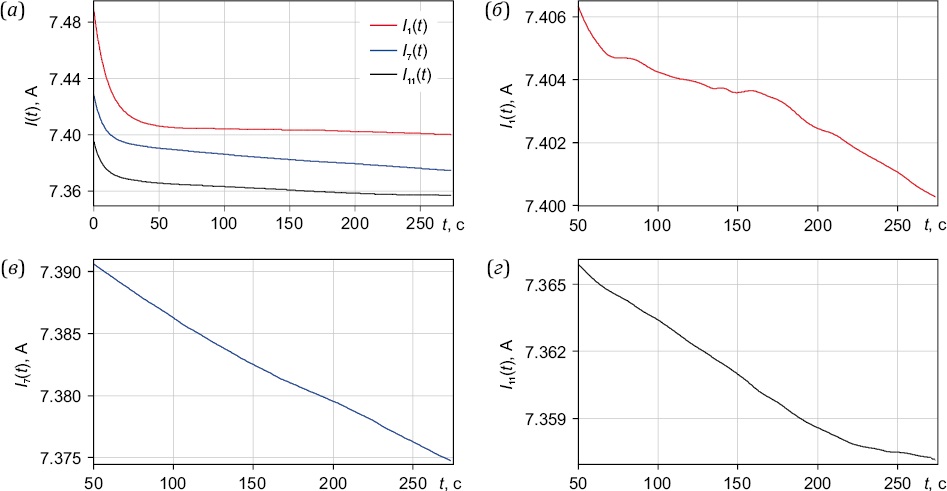
Рис. 2. Графики огибающей зондирующих импульсов тока за все время сеанса зондирования (а) и на более пологом участке для начального I1(t) (б), среднего I7(t) (в) и последнего I11(t) (г) по времени сеансов зондирования.
Fig. 2. Envelope graphs of probing current pulses for the entire duration of the probing session (a) and on a flatter section for the initial I1(t) (б), average I7(t) (в) and the last I11(t) (г) over the duration of the probing sessions.
Согласно рис. 2, а, в измерительных сеансах за время зондирования (длительность сеансов 5 мин) наблюдался достаточно ощутимый (от 1.5 до 3.0 %) спад амплитуды зондирующих импульсов тока в индукционной зондирующей рамке (ИЗР) к концу каждого сеанса. В начале измерительных сеансов амплитуда зондирующих импульсов уменьшается гораздо быстрее, чем в их конце. Такое поведение тока в ИЗР можно объяснить разрядом аккумуляторной батареи и происходящими при этом в каждом отдельно взятом аккумуляторе химическими процессами, а также изменением сопротивления ИЗР и подводящих проводов в процессе их нагрева при подаче тока. Амплитуда формируемых генератором зондирующих сигналов импульсов тока определяется напряжением на зажимах АБ (около 200 В), которое снижается по мере разряда батареи во время сеансов зондирования. Нестационарность амплитуды импульсов тока в ИЗР отражается на регистрируемых измерительными каналами сигналах, так как величина ЭДС, индуцируемая в измерительных катушках датчиков сигналов при проведении сеансов зондирования, прямо пропорциональна амплитуде импульсов тока, подаваемых в ИЗР. Спадающий характер изменения амплитуды зондирующих импульсов тока не меняется от сеанса к сеансу, меняется только скорость и величина спада в зависимости от степени разряда аккумуляторной батареи. На временах t≥50 c (рис. 2, б, г) наблюдается немонотонный характер изменения во времени функции модуля тока I(t). Меняется знак производной dI(t)/dt. Наиболее вероятной причиной такого поведения функции I(t) может быть нестабильность химических процессов, происходящих в силовой аккумуляторной батарее при ее разряде, во время проведения сеансов зондирования земной коры. В традиционном методе работы на выключении тока при вычислении кривой становления поля учитывается одно значение амплитуды тока перед его выключением. При работе в режиме переключения тока изменение его амплитуды (поскольку ток не отключается) влияет на каждый отсчет регистрируемого на приемной стороне сигнала становления поля. Таким образом, возникает острая необходимость в учете изменений амплитуды зондирующих импульсов тока при обработке регистрируемых измерительным комплексом сигналов с целью снижения влияния нестабильности тока в ИЗР на получаемые кривые зондирования.
Предлагаемый метод учета нестабильности амплитуды зондирующих импульсов тока заключается в вычислении корректирующей функции К(t), определяемой как
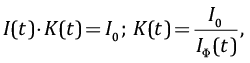
где I(t) – огибающая импульсов тока в ИЗР, получаемая в результате обработки зарегистрированных каналом измерения тока сигналов; I0 – постоянная величина (амплитуда импульсов тока в ИЗР, к которой приводятся сигналы, зарегистрированные измерительными каналами с индукционными датчиками). За I0 было принято максимальное значение амплитуды импульсов тока в ИЗР, зарегистрированных в измерительных сессиях. Пример графика огибающей импульсов тока в ИЗР и рассчитанной с ее помощью корректирующей функции приведен на рис. 3.
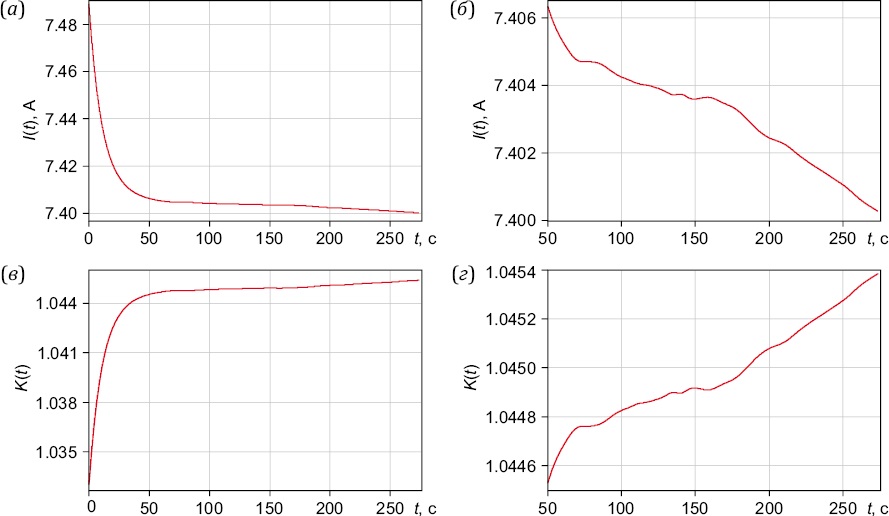
Рис. 3. Расчет корректирующей функции для учета тока в ИЗР: I(t) – огибающая импульсов тока в ИЗР (а, б), K(t) – корректирующая функция (в, г).
Fig. 3. Calculation of the correction function for taking into account the current in the IPL: I(t) is the envelope of the current pulses in the IPL (а, б), K(t) is the correction function (в, г).
В процессе корректировки сигналы, регистрируемые измерительными каналами с индукционными датчиками, умножались на получаемую корректирующую функцию К(t). На рис. 4 приведены фрагменты кривой становления поля без применения корректирующей функции и после ее применения.
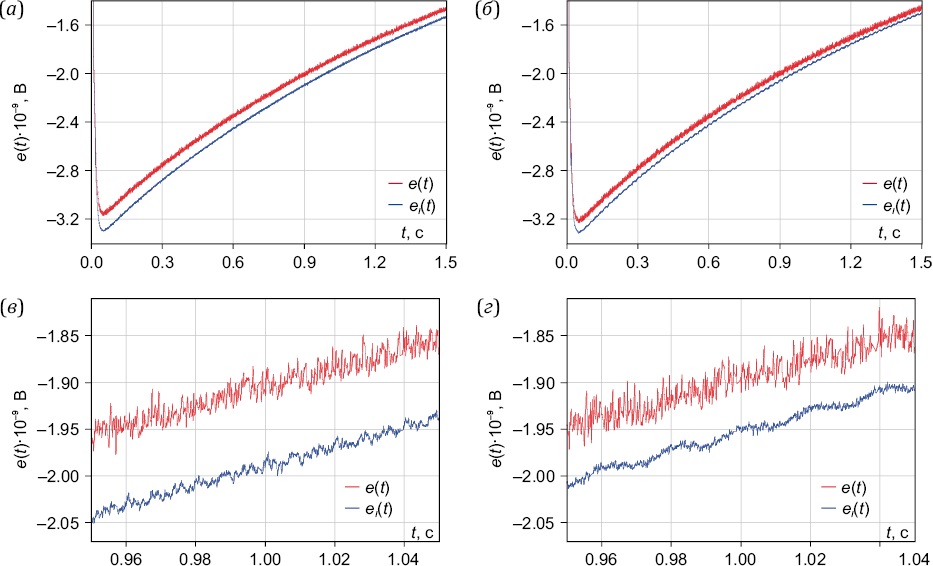
Рис. 4. Фрагменты кривой зондирования до (e(t)) и после (eI(t)) применения корректирующей функции, полученные на измерительных пунктах «МГД» (а, б) и «Чункурчак» (в, г).
Fig. 4. Fragments of the sounding curve before (e(t)) and after (eI(t)) application of the correction function obtained at the measuring points "MGD" (а, б) and "Chunkurchak" (в, г).
Согласно рис. 4, б, г, на кривых зондирования е(t), полученных при обработке сигналов без учета тока в ИЗР, наблюдаются большие остаточные широкополосные помехи по сравнению с кривыми еI(t), полученными с учетом тока в ИЗР. Уровень таких помех на кривых е(t) превышает в несколько раз уровень помех, наблюдаемых на кривых еI(t). Причиной появления такого рода помех может быть особенность (свойство) корреляционной обработки сигналов как сугубо линейной операции с сигналами, заключающаяся в том, что нестационарность зондирующих сигналов и, как следствие, связанная с этим нестационарность принимаемых и регистрируемых измерительными каналами сигналов могут быть эквивалентны внесению в регистрируемые сигналы дополнительных нелинейных искажений. В этом случае, как уже ранее было доказано [Bobrovsky, Ilyichev, 2018; Bobrovsky, 2022], может повышаться уровень так называемых «структурных помех», возникающих при корреляционной обработке сигналов.
Для численной оценки уровня остаточных шумов вычислялись среднеквадратичные значения высокочастотных шумов, наблюдаемых на кривых становления поля, полученных при обработке зарегистрированных в измерительных сеансах сигналов без учета нестабильности тока в зондирующей рамке σ и с учетом нестабильности тока в зондирующей рамке σI (рис. 5). Высокочастотные шумы были получены после удаления из кривых становления поля помех от промышленной силовой сети частотой 50 Гц и низкочастотных составляющих сигналов становления поля. Выделение высокочастотной (шумовой) составляющей сигнала становления поля получается вычитанием из кривой становления поля ее медленно меняющейся (низкочастотной) составляющей и помех от промышленной силовой сети частотой 50 Гц. Низкочастотная составляющая вычисляется с помощью методов полиноминальной аппроксимации высоких порядков (17-й порядок для результатов, приведенных на рис. 5). Большой интерес представляет модификация этих методов, позволяющая повысить точность аппроксимации, которая изложена в работах [Dikusar, 2016; Rababah, 2019; Bénéteau, Centner, 2021]. Такой способ аппроксимации дает хороший результат для больших времен становления поля с медленно меняющейся составляющей. На малых временах, где наблюдается высокая скорость изменения сигнала становления поля, выделение высокочастотной составляющей не представляет интереса, поскольку ее вклад в амплитуду сигнала крайне мал. Помеха 50 Гц получается путем фильтрации сигнала становления поля с удаленной низкочастотной составляющей медианным фильтром Дирихле первого порядка [Gutnikov, 1990], с окном длительностью 1.25 мс.
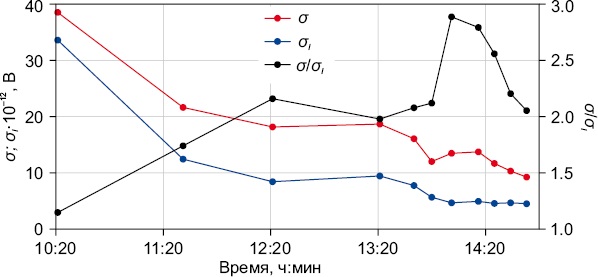
Рис. 5. Среднеквадратичные значения высокочастотных шумов, наблюдаемых на кривых становления поля, полученных при обработке зарегистрированных в измерительных сеансах сигналов без учета нестабильности тока в зондирующей рамке σ и с учетом нестабильности тока в зондирующей рамке σI и их отношения σ/σI (точкой на графиках выделены времена начала сеансов зондирования).
Fig. 5. RMS values of high-frequency noise observed on the field formation curves obtained during processing of signals recorded in measurement sessions without taking into account the instability of the current in the probing frame σ and taking into account the instability of the current in the probing frame σI and their ratio σ/σI (the dot on the graphs indicates the start times of the probing sessions).
Из рис. 5 видно, что при выполнении операции учета нестабильности тока зондирующих импульсов уровень высокочастотных шумов уменьшается, а следовательно, повышается соотношение сигнал – помеха в получаемых кривых зондирования, особенно на больших временах становления поля. Косвенно применение описанных выше процедур позволяет контролировать состояние применяемых аккумуляторов, поскольку со временем аккумуляторы изнашиваются и это может отражаться на получаемых результатах.
3.2. Улучшение методики получения геоэлектрических характеристик среды в рамках модели с проводящей S плоскостью
Для первичной оценки геоэлектрического разреза в условиях полевого эксперимента можно воспользоваться кривыми Sτ(hτ), как описано в работе [Khmelevsky at al., 2005]. Графики зависимостей кажущейся удельной проводимости Sτ и кажущейся глубины погружения проводящей пленки hτ получаются путем решения обратной задачи ЗСБ в рамках модели с проводящей S плоскостью. «Проводящая горизонтальная плоскость в непроводящей среде – единственный вид разреза, для которого удается выразить становление поля через элементарные функции…» [Sidorov, 1985, с. 27]. Как следствие, для данной модели среды возможно приближенное решение обратной задачи ЗСБ без решения прямой задачи. Авторами были рассмотрены методики расчета кажущейся проводимости и кажущейся глубины погружения проводящей пленки на основе работ [Sidorov, 1985; Zhdanov, 1986].
Формула расчета ЭДС индукции в приемной горизонтальной петле, приведенная в работе [Zhdanov, 1986], выводится из закона электромагнитной индукции Фарадея 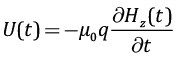 и расчета скорости
и расчета скорости  изменения вертикальной компоненты вектора Hz напряженности магнитного поля, в условиях ближней зоны. В результате модуль ЭДС вычисляется по формуле:
изменения вертикальной компоненты вектора Hz напряженности магнитного поля, в условиях ближней зоны. В результате модуль ЭДС вычисляется по формуле:
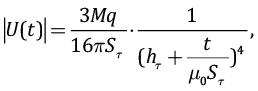
где M=I∙Q – момент тока в генераторной петле; I – амплитуда тока, Q – эквивалентная площадь генераторной петли; q – эквивалентная площадь приемной петли; Sτ – кажущаяся продольная проводимость пленки; hτ – глубина погружения пленки; t – время, в течение которого рассматривается процесс становления поля; μ0 – абсолютная магнитная проницаемость среды, принятая в отсутствие ферромагнетиков равной магнитной проницаемости вакуума 4π⋅10⁻⁷ Гн/м.
При двух неизвестных Sτ(t) и hτ(t) недостаточно одного уравнения, поэтому дифференцированием U(t) по времени t получим второе уравнение для 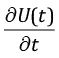 :
:
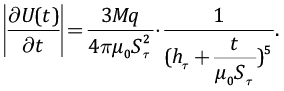
Решая систему из двух уравнений с двумя неизвестными, получим:
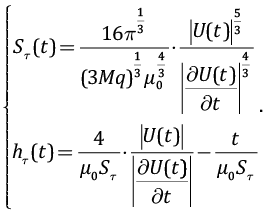
В работе [Sidorov, 1985] формула расчета ЭДС индукции в приемной круговой петле радиуса r представлена в следующем виде:

где
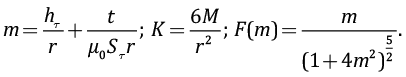
Очень важную роль в дальнейших рассуждениях играет параметр m, имеющий размерность длины. Выполнив ряд преобразований, получим следующее уравнение:
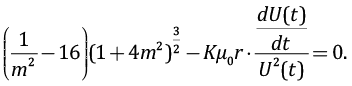
Численно решая его относительно m, получим для каждого момента времени t значение m(t). Зная m(t), находим:
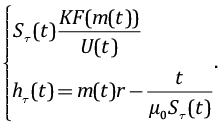
Для дальнейшего анализа обе методики были реализованы в программном обеспечении ЭРК ШПС. Примеры расчета проводимости Sτ(t) и глубины hτ(t), выполненного при помощи реализованных алгоритмов, приведены на рис. 6.
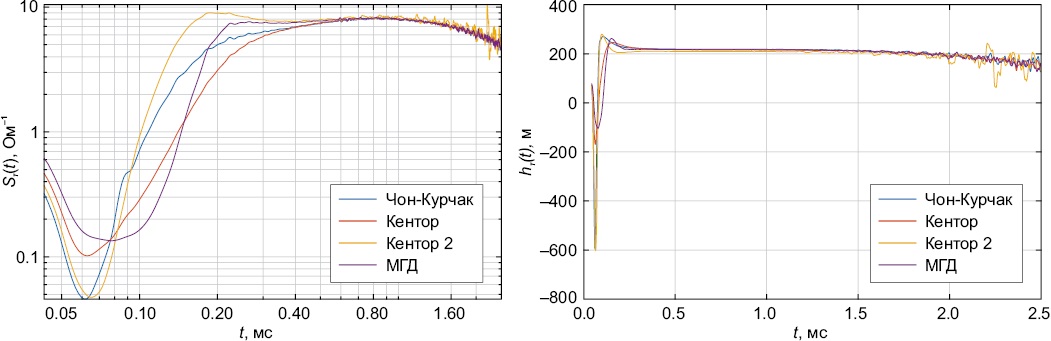
Рис. 6. Расчеты проводимости Sτ(t) и глубины hτ(t) для исходных данных U(t), полученных на четырех измерительных точках, расположенных на территории Бишкекского геодинамического полигона.
Fig. 6. Calculations of conductivity Sτ(t) and depth hτ(t) for the initial data U(t), obtained at four measuring points located on the territory of the Bishkek geodynamic test site.
Результаты расчетов для полевых данных показали, что относительное отклонение величин Sτ(t) и hτ(t), рассчитанных по методике М.С. Жданова, от величин, рассчитанных по методике В.А. Сидорова, составляет меньше 1 %.
Для проверки и тестирования данных методик на основе работы [Sidorov, 1985] был разработан и реализован в программном обеспечении ЭРК ШПС алгоритм решения прямой задачи ЗСБ.
Для решения прямой задачи электроразведки задают ряд значений глубины исследования Hi. Разрез от земной поверхности до глубины Hi заменяют более простой моделью – эквивалентной плоскостью, считая остальную часть разреза изолятором. Для такой модели рассчитывают кривую становления. Получив семейство кривых при разных значениях Hi, по огибающей семейства находят окончательную кривую становления поля.
Для произвольного слоистого разреза задается глубина залегания эквивалентной плоскости h как средневзвешенная из глубин элементарных тонких слоев, слагающих разрез:

где σ(z) – удельная проводимость разреза как функция глубины z, заданная кусочно-постоянной функцией (нормальная модель) или гладкой функцией (градиентная модель); S – интегральная продольная проводимость слоистого разреза; H – мощность слоистого разреза; ɡ – параметр, определяющий относительный вес верхних и нижних горизонтов при подсчете h (ɡ>0). При задании глубины h таким образом выполняется неравенство 0≤h≤H, причем h тяготеет к значению глубины центра проводимости разреза. Заметим, что если члены наперед заданной последовательности глубин Hi задаются линейным образом, т.е. Hi+1=Hi+dH, то график значений параметра m=m(i) от i при ɡ, близком к 1, приближается к прямой, а при ɡ=1 целиком ложится на нее (рис. 7).
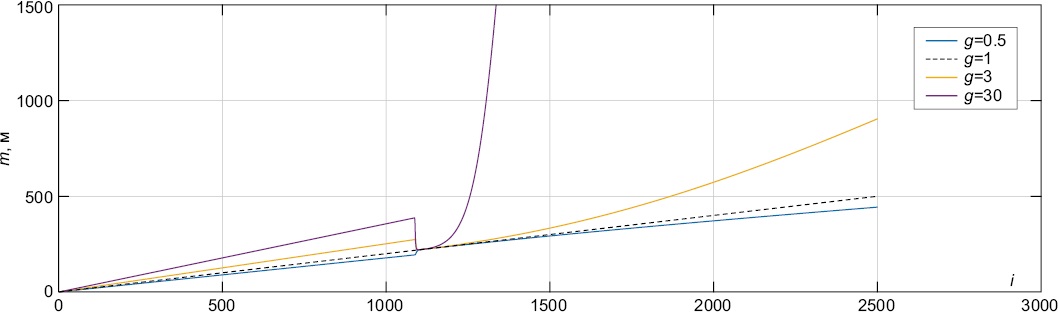
Рис. 7. График зависимости m от i при решении прямой задачи для различных ɡ.
Fig. 7. Graph of the dependence of m on i when solving the direct problem for different ɡ.
Решения прямой задачи Eφ(t), Bz(t), U(t) при ɡ, близком к 1 (ɡ≈1), лучше всего описывают поведение реальной кривой становления поля (ɡ(1)=0.5; ɡ(2)=1; ɡ(3)=3; ɡ(4)=30) (рис. 8).
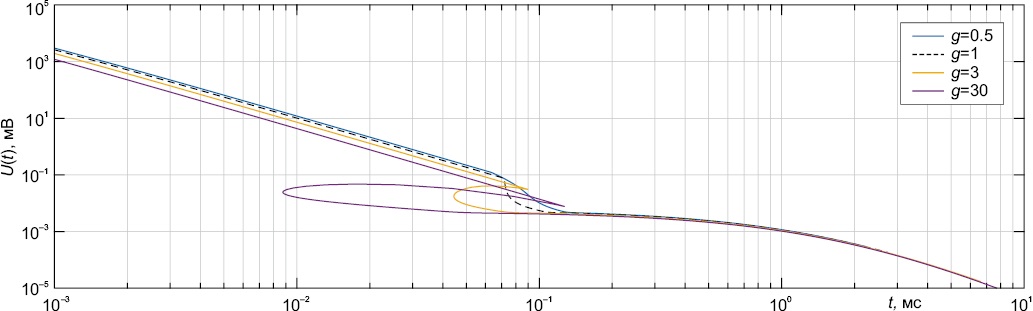
Рис. 8. Сравнение графиков становления поля, полученных при решении прямой задачи при различных значениях ɡ.
Fig. 8. Comparison of field formation graphs obtained by solving the direct problem for different values of ɡ.
Таким образом, как при решении прямой задачи, так и при решении обратной задачи методом подбора оправдан выбор параметра ɡ, близкого к 1 (ɡ≈1). Тогда зависимость параметра m=m(i) от i близка к линейной, а сам параметр m отражает глубину исследования, т.е. H≈m.
Сравним поведение параметра m при решении прямой задачи с поведением m при решении обратной задачи. Для этого для произвольного разреза, например для разреза, заданного распределением:

решим прямую задачу при ɡ≈1 и примем это решение в качестве эталона (рис. 9).
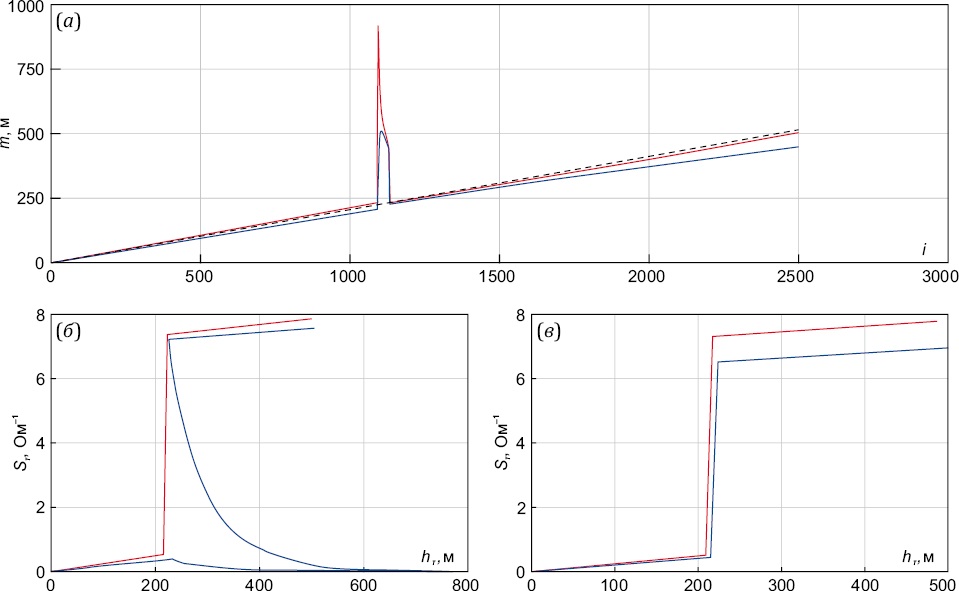
Рис. 9. Сравнение эталонной зависимости Sτ(hτ) (красный цвет) с зависимостью Sτ(hτ) при решении обратной задачи (синий цвет) до (б) и после (в) сглаживания параметра m (а).
Fig. 9. Comparison of the reference dependence Sτ(hτ) (red) with the dependence Sτ(hτ) when solving the inverse problem (blue) before (б) and after (в) smoothing the parameter m (a).
Теперь найденное решение прямой задачи U(t) возьмем в качестве исходных данных для решения обратной задачи. График параметра m при решении обратной задачи для указанных значений ɡ приведен на рис. 9, а. Решение обратной задачи по данной методике дает сбои при резком скачке кажущейся удельной проводимости. Это проявляется в форме скачков производной становления поля или скачков параметра m (рис. 9, а). При этом в результате решения обратной задачи для эталонного разреза (полученного при решении прямой задачи) наблюдается странное поведение графика зависимости Sτ(hτ) (рис. 9, б).
Таким образом, улучшение методики может состоять либо в сглаживании производной от функции становления поля,  , либо в сглаживании параметра m. Сглаживание производной
, либо в сглаживании параметра m. Сглаживание производной 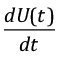 представляет собой сложную задачу, поскольку сложно предсказать аппроксимирующую ее функцию. Для сглаживания же функции m=m(x) можно выбрать, например, аппроксимирующую функцию в форме
представляет собой сложную задачу, поскольку сложно предсказать аппроксимирующую ее функцию. Для сглаживания же функции m=m(x) можно выбрать, например, аппроксимирующую функцию в форме 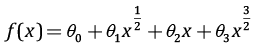 , которая при некотором наборе коэффициентов {θi} может быть линейной функцией (на рис. 9, а, показана штриховой линией). По-разному сглаживая параметр m, можно добиться разной степени приближения полученной зависимости Sτ(hτ) к эталонной (рис. 9, в). При этом нужно помнить, что решения прямой и обратной задачи являются асимптотическими и имеют погрешности в приближении ближней зоны. Следует отметить, что такой вариант улучшения применим только к варианту решения обратной задачи ЗСБ, предложенному В.А. Сидоровым, поэтому данный вариант решения принят в программном обеспечении ЭРК ШПС в качестве основного.
, которая при некотором наборе коэффициентов {θi} может быть линейной функцией (на рис. 9, а, показана штриховой линией). По-разному сглаживая параметр m, можно добиться разной степени приближения полученной зависимости Sτ(hτ) к эталонной (рис. 9, в). При этом нужно помнить, что решения прямой и обратной задачи являются асимптотическими и имеют погрешности в приближении ближней зоны. Следует отметить, что такой вариант улучшения применим только к варианту решения обратной задачи ЗСБ, предложенному В.А. Сидоровым, поэтому данный вариант решения принят в программном обеспечении ЭРК ШПС в качестве основного.
4. ЗАКЛЮЧЕНИЕ
Регистрация амплитуды зондирующих импульсов тока в ИЗР и учет ее при корреляционной обработке зарегистрированных ЭРК ШПС сигналов, помимо нормировки получаемых кривых зондирования (приведение их к заданному значению амплитуды зондирующих сигналов), обеспечивает значительное, в несколько раз, повышение соотношения сигнал – помеха в получаемых кривых зондирования, особенно на больших временах становления поля.
Разработанные и реализованные в программном обеспечении ЭРК ШПС алгоритмы решения обратной и прямой задачи ЗСБ позволят в дальнейшем перейти к реализации более сложных алгоритмов интерпретации данных полевых экспериментов с ЭРК ШПС с целью получения геоэлектрического разреза.
Предложен способ улучшения метода решения обратной задачи ЗСБ, в рамках модели с проводящей S плоскостью, позволяющий повысить достоверность получаемых результатов. Способ основан на сглаживании модельного параметра m=hτ+t/µSτ, имеющего размерность длины, где hτ и Sτ – соответственно кажущаяся глубина и кажущаяся продольная проводимость плоскости. Первичное решение обратной задачи с предложенным улучшением позволяет оценить интервалы значений параметров геоэлектрического разреза (мощность слоев и их удельная проводимость) для дальнейшего, более точного, решения обратной задачи методом подбора в установленных интервалах значений параметров геоэлектрического разреза.
5. БЛАГОДАРНОСТИ
Авторы выражают благодарность Д.М. Авдюхову и Е.В. Вихрову за помощь в разработке алгоритмов решения прямой и обратной задачи ЗСБ.
6. ЗАЯВЛЕННЫЙ ВКЛАД АВТОРОВ / CONTRIBUTION OF THE AUTHORS
Авторы внесли эквивалентный вклад в подготовку рукописи, прочли и одобрили финальную версию перед публикацией.
Both authors made an equivalent contribution to this article, read and approved the final manuscript.
7. РАСКРЫТИЕ ИНФОРМАЦИИ / DISCLOSURE
Авторы заявляют об отсутствии конфликта интересов, связанного с этой рукописью.
Both authors declare that they have no conflicts of interest relevant to this manuscript.
Список литературы
1. Bénéteau C., Centner R., 2021. A Survey of Optimal Polynomial Approximants, Applications to Digital Filter Design, and Related Open Problems. Complex Analysis and Its Synergies 7, 16. https://doi.org/10.1007/s40627-021-00068-x.
2. Бобровский В.В. Особенности корреляционной обработки шумоподобных сигналов в электроразведочной аппаратуре // Геофизические исследования. 2022. T. 23. № 2. С. 39–54]. https://doi.org/10.21455/gr2022.2-3.
3. Бобровский В.В., Ильичев П.В. Математическое моделирование предполагаемых источников (причин) «структурных помех» в геоэлектроразведчной аппаратуре с шумоподобными зондирующими сигналами // Проблемы геодинамики и геоэкологии внутриконтинентальных орогенов: Материалы докладов VII Международного симпозиума (19–24 июня 2017 г.). Бишкек: НС РАН, 2018. C. 360–370].
4. Бобровский В.В., Ильичёв П.В., Александров П.Н. Методика получения геоэлектрических характеристик среды в экспериментальном электроразведочном комплексе с шумоподобными сигналами // Приборы и системы разведочной геофизики. 2023. Т. 78. № 3. С. 93–100].
5. Bobrovsky V.V., Ilyichev P.V., Lashin O.A., 2021. Broadband Measuring Complex with Pseudonoise Signals for Electromagnetic Monitoring of Modern Geodynamic Processes in Seismically Active Zones. Seismic Instruments 57, 384–396. https://doi.org/10.3103/S0747923921040034.
6. Бобровский В.В., Ильичев П.В., Лашин О.А., Лисимов М.О. Технология активного электромагнитного мониторинга геодинамических процессов в сейсмоактивных зонах Северного Тянь-Шаня // Наука и технологические разработки. Т. 102. № 2/3. С. 40–62]. https://doi.org/10.21455/std2023.2-3-2.
7. Dikusar N.D., 2016. Higher-Order Polynomial Approximation. Mathematical Models and Computer Simulations 8, 183–200. https://doi.org/10.1134/S2070048216020058.
8. Duncan P.M., Hwang A., Edwards R.N., Bailey R.C., Garland G.D., 1980. The Development and Applications of a Wide Band Electromagnetic Sounding System Using Pseudo-Noise Source. Geophysics 45 (8), 1276–1296. https://doi.org/10.1190/1.1441124.
9. Гантмахер В.Е., Быстров Н.Е., Чеботарев Д.В. Шумоподобные сигналы. Анализ, синтез, обработка. СПб.: Наука и техника, 2005. 396 с.].
10. Goncharov А.А., Alekseev D.А., Koshurnikov А.V., Gunar A.Yu., Semiletov I.P., Pushkarev P.Yu., 2022. Using Pseudo-Random Code Sequences for Improving the Efficiency of Near-Field Transient Electromagnetic Sounding on the Arctic Shelf. Izvestiya, Physics of the Solid Earth 58, 744–754. https://doi.org/10.1134/S1069351322050020.
11. Гутников В.С. Фильтрация измерительных сигналов. Л.: Энергоатомиздат, 1990. 193 с.].
12. Ilyichev P.V., Bobrovsky V.V., 2015. Application of Pseudonoise Signals in Systems of Active Geoelectric Exploration (Results of Mathematical Simulation and Field Experiments). Seismic Instruments 51, 53–64. https://doi.org/10.3103/S0747923915010089.
13. Электроразведка: Пособие по электроразведочной практике для студентов геофизических специальностей / Ред. В.К. Хмелевский, И.Н. Модин, А.Г. Яковлев. М.: ГЕРС, 2005. 311 с.].
14. Rababah A., 2019. High Order Approximation of Degree Nine and Order Eighteen. Journal of Inequalities and Applications 2019, 115. https://doi.org/10.1186/s13660-019-2103-x.
15. Сидоров В.А. Импульсная индуктивная электроразведка. М.: Недра, 1985. 192 c.].
16. Светов Б.С. Электромагнитный мониторинг сейсмотектонических процессов // Известия вузов. Геология и разведка. 1992. № 2. С. 99–116].
17. Светов Б.С., Алексеев Д.А., Агеев В.В., Каринский С.Д., Яковлев А.Г. Применение шумоподобных сигналов в зондированиях становлением поля // Геофизика. 2012. № 1. С. 52–60].
18. Тикшаев В.В. Высокоразрешающая электроразведка становлением поля с пространственным накоплением для поисково-разведочных работ на нефть и газ: Дис. … докт. тех. наук. М., 1984. 446 с.].
19. Варакин Л.Е. Системы связи с шумоподобными сигналами. М.: Радио и связь, 1985. 384 с.].
20. Великин А.Б., Великин А.A. Новый корреляционный метод импульсной электроразведки с шумоподобными сигналами СТЕМ для электромагнитного зондирования недр при поисках углеводородного сырья // Вопросы естествознания. 2016. Т. 1. № 19. C. 103–115].
21. Zepernick H.-J., Finger A., 2005. Pseudo Random Signal Processing. Theory and Application. John Wiley & Sons, 432 p. DOI:10.1002/9780470866597.
22. Жданов М.С. Электроразведка. М.: Недра, 1986. 316 с.].
Об авторах
В. В. БобровскийКыргызстан
720049, Бишкек
П. В. Ильичев
Кыргызстан
720049, Бишкек
Дополнительные файлы
Рецензия
Для цитирования:
Бобровский В.В., Ильичев П.В. ОСОБЕННОСТИ ПОЛУЧЕНИЯ ГЕОЭЛЕКТРИЧЕСКИХ ХАРАКТЕРИСТИК СРЕДЫ В ЭКСПЕРИМЕНТАЛЬНОМ ЭЛЕКТРОРАЗВЕДОЧНОМ КОМПЛЕКСЕ С ШУМОПОДОБНЫМИ СИГНАЛАМИ. Геодинамика и тектонофизика. 2025;16(2):0820. https://doi.org/10.5800/GT-2025-16-2-0820. EDN: NUFKJW
For citation:
Bobrovsky V.V., Ilyichev P.V. FEATURES OF OBTAINING GEOELECTRIC CHARACTERISTICS OF THE ENVIRONMENT IN AN EXPERIMENTAL ELECTRICAL PROSPECTING COMPLEX WITH PSEUDONOISE SIGNALS. Geodynamics & Tectonophysics. 2025;16(2):0820. (In Russ.) https://doi.org/10.5800/GT-2025-16-2-0820. EDN: NUFKJW




















































