Перейти к:
О ВОЗМОЖНОМ МЕХАНИЗМЕ ОБРАЗОВАНИЯ ОТКРЫТОЙ ТРЕЩИНОВАТОСТИ В ОСАДОЧНЫХ БАССЕЙНАХ
https://doi.org/10.5800/GT-2024-15-2-0754
EDN: GJZCIS
Аннотация
В работе показано, что формирование ортогональных систем открытых макротрещин (отрывы) осадочных бассейнов может происходить на стадии диагенеза за время в первые сотни лет для небольшого диапазона глубин шельфа (до 100 м) в процессе осадконакопления. В этот период идет вязкое изотропное уплотнение осадков и медленное отжатие излишков воды, определяющее уменьшение упругого коэффициента Пуассона от значений, близких к 0.5, до значений 0.3–0.2. Из-за этого в осадках, напряженное состояние которых практически полностью определяется только силой тяжести вышележащих пород, происходит снижение на 50 % и более уровня напряжений горизонтального сжатия от начального литостатического уровня давления. С другой стороны, в случае достижения предела псевдопластического течения в породе происходит вертикальное уплотнение, сопровождающееся ростом горизонтального сжатия. Эти два конкурирующих процесса вместе с фактором флюидного давления в трещинах и порах определяют возможность формирования хрупких трещин отрыва. Показано, что в породах, имеющих низкий уровень предела текучести (глины), уплотнение на стадии псевдопластического течения приводит к повышению уровня напряжений горизонтального сжатия, из-за чего хрупкое разрушение в них на стадии диагенеза становится невозможным. В породах, обладающих высоким уровнем сдвиговой прочности (песчаник, известняк), хрупкое разрушение из-за превышения давления воды в субвертикальных микротрещинах начинается раньше, чем достижение предела текучести.
Для цитирования:
Ребецкий Ю.Л. О ВОЗМОЖНОМ МЕХАНИЗМЕ ОБРАЗОВАНИЯ ОТКРЫТОЙ ТРЕЩИНОВАТОСТИ В ОСАДОЧНЫХ БАССЕЙНАХ. Геодинамика и тектонофизика. 2024;15(2):0754. https://doi.org/10.5800/GT-2024-15-2-0754. EDN: GJZCIS
For citation:
Rebetsky Yu.L. ON THE POSSIBLE FORMATION MECHANISM OF THE OPEN FRACTURING IN SEDIMENTARY BASINS. Geodynamics & Tectonophysics. 2024;15(2):0754. (In Russ.) https://doi.org/10.5800/GT-2024-15-2-0754. EDN: GJZCIS
1. ВВЕДЕНИЕ
В поисковой нефтегазовой геологии при прогнозе коллекторов – участков повышенной трещинной пористости пород – существует проблема объяснения механизма возникновения систем трещин, формирующих закономерную блоковую структуру в компетентных слоях осадочных бассейнов (рис. 1, а). Данная проблема актуальна прежде всего как прикладная задача геодинамики и поисковой геологии. Но она также может рассматриваться как фундаментальная проблема геомеханики и тектонофизики.
В известняках и доломитах эти трещины, являясь отрывными, перпендикулярны к слоистости; в песчаниках, наряду с такими трещинами, наблюдаются также и наклонные (рис. 1, б). В мергелях, глинах и опоках наиболее характерными являются трещины, ограничивающие скорлуповатые и оскольчатые отдельности. Замечено, что вертикальные трещины встречаются в более прочных осадочных породах и поэтому в известняке и особенно в песчанике их проявление зависит от существующих в них примесей. Наличие примесей глин уменьшает вероятность возникновения таких трещин. Густота трещин зависит также от мощности пласта. Среднее расстояние между трещинами отрыва внутри одного слоя примерно равно удвоенной мощности слоя. Характерной особенностью таких трещин является то, что они обычно развиты в каждом слое отдельно. Первоначально они могут быть скрытыми, но если порода попадает в зону выветривания, трещины раскрываются и разделяют породу на хорошо выраженные блоки отдельностей – геометрически правильных штуфов горной породы (прямоугольная, кубическая, параллелепидальная, призматическая) [Twiss, Moores, 1992; Mandl, 2005; Frolov, 1992, 1993, 1995; Epifantsev, Pletenchuk, 2008].
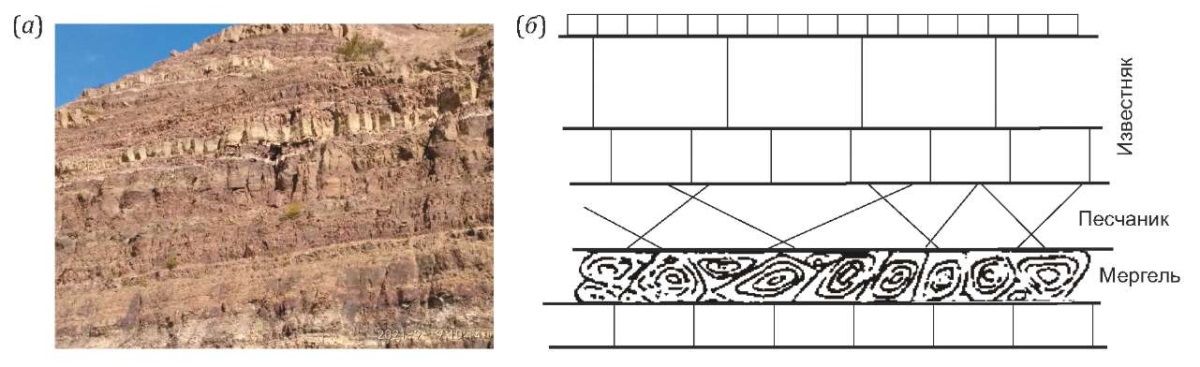
Рис. 1. Примеры систем ортогональных вертикальных трещин отрыва (о. Сахалин) (а) и обобщение расположения литогенетических систем трещин в смежных слоях осадочных пород разного типа (рисунок из работы [Epifantsev, Pletenchuk, 2008]) (б).
Fig. 1. Examples of orthogonal vertical fracture systems (Sakhalin Island) (a) and generalization of the location of lithogynetic fracture systems in adjacent layers of sedimentary rocks of different types (figure from [Epifantsev, Pletnechuk, 2008]) (б).
Период формирования рассматриваемого типа трещин часто связывают с процессом диагенеза – диагенетические или литогенетические трещины [Epifantsev, Pletenchuk, 2008; Strikha, 2012]. В рамках такого подхода эти трещины именуются первичными и относятся к нетектоническим. Их образование обусловлено изменениями внутренних свойств пород под влиянием сил, проявляющихся при экзогенных процессах на поверхности Земли или вблизи нее. В геологии осадочных пород считается, что формирование первичных диагенетических трещин происходит за счет сокращения объема осадков. Иногда даже говорят о генезисе первичных трещин как трещин усыхания. В некоторых монографиях имеется уточнение, что уменьшение объема осадка в связи с потерей воды вызывает проявление растягивающих усилий, в результате которых и образуются трещины [Olkhovatenko et al., 2015].
Если согласиться с этой гипотезой и полагать, что механизмом формирования систем трещин отрыва в осадочной породе является ее усыхание, то тогда можно использовать хорошо известные выводы по механизму возникновения трещин в высыхающих влажных илистых отложениях. В усыхающих илах растягивающие напряжения возникают прежде всего на поверхности отложений и сразу под ними, потому что потеря объема там наибольшая (практически полное обезвоживание), в то время как материал ниже высыхает и сжимается медленнее. Из-за этого в приповерхностной части слоя могут возникнуть дополнительные горизонтальные растягивающие напряжения. Когда эти дополнительные напряжения превысят напряжения сжатия от действия массовых сил (для влажных осадков напряженное состояние приблизительно изотропное), на поверхности осадка развиваются трещины отрыва, образуя полигональную сеть. Усадочные трещины возникают также в магматических породах. Но в них развитие таких трещин происходит за счет объемной усадки, вызванной охлаждением.
Следует заметить, что при приложении такого механизма формирования трещин к породам осадочных бассейнов сразу возникает противоречие. Породы, обладающие коллекторскими свойствами в виде изучаемых систем трещин отрыва, часто наблюдаются в шельфовой зоне, которая не была на поверхности, т.е. осадочные породы с такими системами трещин не могли проходить стадию усыхания за счет практически полного удаления воды. Насыщенность водой в таких осадках уменьшается, но она остается в них в достаточно большом объеме. Также необходимо отметить, что процесс литификации осадков в условиях шельфа предполагает достаточно интенсивное их пластическое уплотнение, вызываемое весом вышележащего слоя воды (десятки – первые сотни метров, чему соответствует вертикальное давление от первых бар до десятков бар). В таком случае изменение объема полутвердой фазы осадков не будет приводить к латеральному укорочению и появлению дополнительных растягивающих напряжений, как это имеет место в высыхающих илах в приповерхностных условиях.
В работах [Mikhailov, 1956; Seminsky, 2003] возможность возникновения в приповерхностных условиях парагенезиса вертикальных систем трещин с ориентацией, близкой к ортогональной, связывалась с горизонтальным удлинением, создающим истинное растяжение в породе. Такой механизм объяснялся региональным деформационным процессом (например, растяжением фундамента осадочного бассейна). Однако он требует достаточно специфических условий регионального деформирования, при которых разница в латеральных напряжениях была бы достаточно небольшой и напряжения сжатия от массовых сил не превышали бы уровень напряжений растяжения тектонического генезиса. Предполагается, что в этом случае системы трещин отрывов возникают не одновременно, а последовательно, что приводит к переиндексации напряжений и возможности возникновения истинного растяжения в другом, ортогональном первому, направлении. Такой механизм, вероятно, может иметь место, но им трудно объяснить столь распространенное явление, как первичная трещиноватость.
Во второй половине ХХ в. изучение обсуждаемых систем трещин становится чрезвычайно актуальным в нефтяной и газовой добыче из-за их роли в поведении коллектора [Pollard, Aydin, 1988]. Расшифровка генезиса систем трещин отрыва и прогноз мест их расположения помогли бы в безаварийной проходке и завершении бурения скважин, а также при прогнозе объемов месторождений.
В работах [Hubbert, Willis, 1957; Handin et al., 1963; Secor, 1965] было высказано предположение, что механизм образования таких трещин может быть связан с давлением воды в порах и микротрещинах, превышающим уровень напряжений сжатия, нормальных к развивающейся макротрещине. Механизм формирования подобных условий связывали с действием массовых сил тяжести без приложения внешних граничных сил [Engelder, 1985; Engelder, Lacazette, 1990; Lacazette, Engelder, 1992; Cosgrove, 2001; Aydin, 2014; Fall et al., 2015], а возможность достижения аномального повышенного давления поровой жидкости в коллекторах из песчаника объясняли термокаталитической генерацией газа в прослоях богатых органикой сланцев и углей и сопутствующей миграцией газа в соседние залежи песчаника [Spencer, 1987; Lorenz, Finley, 1991; Cumella, Scheevel, 2008; Yurewicz et al., 2003]. Такой процесс образования трещины за счет естественного увеличения давления поровой жидкости до аномально высоких значений ранее назывался естественным гидравлическим разрывом пласта [Engelder, 1985].
Следует заметить, что в российских университетских курсах по структурной геологии отсутствуют положения этой теории формирования систем отрывных трещин, а есть только упоминание о трещинах усыхания. С другой стороны, существуют также работы, например [Chemenda, 2019; Guo et al., 2017], в которых формирование систем отрывных трещин в осадочных бассейнах связывают с процессами деформирования пород, происходящими после диагенеза.
В работах А.И. Шеменды [Chemenda, 2019; Chemenda et al., 2021] формирование таких трещинных структур является результатом горизонтального растяжения, возникающего в процессе вертикального расплющивания компетентного слоя (задавались вертикальные скорости деформаций), зажатого в пачке между двумя некомпетентными слоями. Эффективные горизонтальные напряжения на торцах пачки слоев предполагаются равными нулю, что интерпретируется как наличие здесь трещин отрыва. При этом внутри компетентного слоя за счет действия касательных напряжений на границе контакта с некомпетентными слоями формируются сжимающие напряжения, превосходящие заданное флюидное давление. Считается, что в процессе горизонтального растяжения в породе достигается предельное состояние пластического деформирования и хрупкого разрушения (локализованное растяжение). Результаты численного геомеханического расчета показали, что в слое возникает вертикальная система трещин с шагом, зависящим от мощности компетентного слоя, и эта зависимость существенно нелинейная. Принятые значения компетентного слоя (известняка) отвечали породе, завершившей процесс литификации (прочность на отрыв σt=7 МПа, прочность на сжатие σc=60 МПа, модуль упругости 20 ГПа, коэффициент Пуассона 0.25). Вертикальные напряжения имели порядок литостатического давления на глубине 700 м.
Такой подход к процессу трещинообразования прямо определяет, что внешние условия нагружения приводят к появлению в компетентном слое растягивающих напряжений именно в твердом каркасе пород. Следует отметить, что прямая взаимосвязь возникновения трещин отрыва в компетентном слое с действием касательных напряжений вдоль границ с некомпетентными слоями отвергает возможность возникновения ортогональной системы отрывов (блочность). По этим же причинам такой механизм не может объяснить смещенные по латерали системы отрывов для контактирующих компетентных слоев.
Поскольку множество геологических данных, обобщенных в курсах по структурной геологии [Epifantsev, Pletenchuk, 2008; Strikha, 2012; Olkhovatenko et al., 2015], говорит о ранней стадии формирования систем трещин отрывов (первичная трещиноватость), задачей представляемых исследований являлось обоснование механизма их формирования в компетентном слое многослойной пачки в рамках концепции о естественном гидроразрыве породы, происходящем в процессе диагенеза. При этом ключевым моментом этого обоснования является установление причин отсутствия субвертикальных трещин отрыва в сопряженных некомпетентных слоях.
2. НАЧАЛЬНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ ПРИ ДИАГЕНЕЗЕ
Рассмотрим поведение модели под нагрузкой, вызванной только действием собственного веса, осадочного слоя в приповерхностных условиях (глубина не более 10–50 м), который находится в начальной стадии диагенеза (катагенеза). В начале процесса литификации параметры прочности породы соответствуют очень слабым породам (менее 0.1 МПа), а коэффициент Пуассона близок к υ≈0.5 из-за высокой влагонасыщенности. Считается, что в процессе литификации его прочность может возрасти на порядок, а в результате вязкого всестороннего уплотнения, приводящего к уменьшению объема пор и выдавливанию из породы воды, коэффициент Пуассона может понизиться до значений υ=0.2–0.3.
Поскольку при υ≈0.5, начальное напряженное состояние близко к изотропному (вертикальные и горизонтальные напряжения равны), поведение слоя подобно упругой несжимаемой жидкости. По мере того как значение коэффициента Пуассона будет снижаться, уровень напряжений горизонтального сжатия, вызванного только действием массовых сил тяжести, также будет уменьшаться. Таким образом, исследуемой стадии процесса будет отвечать режим напряженного состояния горизонтального растяжения, при котором уровень горизонтального сжатия меньше уровня вертикальных сжимающих напряжений. Следует отметить, что термин «горизонтальное растяжение» относится к характеристике напряженного состояния и не означает, что в латеральном направлении имеют место деформации удлинения. При формировании осадков на субгоризонтальном океаническом дне в первом приближении общие (упругие и пластические) латеральные деформации слоя близки к нулю.
Таким образом, можно полагать, что в слое имеет место плоская деформация, при которой в двух ортогональных латеральных направлениях отсутствуют деформации в масштабе слоя (нет его общего удлинения или укорочения). Далее напряжения и деформации, отвечающие этому положению, будут именоваться макроскопическими. Вертикальные напряжения равны весу вышележащего столба горной породы (с учетом водонасыщенности):
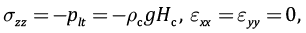 (1)
(1)
где ρc g – произведение средней плотности вышележащих пород на ускорение свободного падения, глубина Hc – срединная линия слоя от морского дна. Здесь и далее отрицательный знак нормальных напряжений отвечает напряжениям сжатия, а положительный – напряжениям растяжения. Можно считать, что толщина водного слоя над морским дном мала (первые десятки метров), и его давлением пока будем пренебрегать.
На начальной стадии диагенеза, когда разница между вертикальными и горизонтальными напряжениями невелика, имеет место упругое состояние, поэтому горизонтальные напряжения определяются согласно [Dinnik, 1926; Jager, 1962; Price, Cosgrove, 1990] из условия горизонтального стеснения (второе выражение в (1)) и закона Гука в виде выражений:
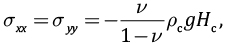 (2)
(2)
где υ – коэффициент Пуассона, ρc – плотность пород исследуемого слоя, которая близка к плотности вышележащих пород ( g – ускорение свободного падения).
Мощность самого слоя hc (порядка метра или менее) мала в сравнении с глубиной его расположения Hc (в расчетах авторов глубина меняется в диапазоне 20–300 м), и поэтому изменением напряжений в слое по его толщине можно пренебречь. Касательные напряжения в принятой системе координат отсутствуют:
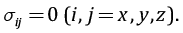
На основе выражений (2) можно оценить изменение напряжений горизонтального сжатия при уменьшении значений коэффициента Пуассона от 0.5 до 0.2, которое составит 75 % (от –ρc gHc до –0.25 ρc gHc).
3. УСЛОВИЯ ХРУПКОГО РАЗРУШЕНИЯ В СЛОИСТОЙ ПАЧКЕ
В осадочных бассейнах, формирующихся в водной среде в микротрещинах породы, всегда присутствует вода (ρfl – плотность), создающая на стенках трещин давление
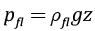 , (3)
, (3)
которое уменьшает боковое обжатие в микротрещинах и порах, вызываемое горизонтальными сжимающими напряжениями σxx, σyy, что может способствовать развитию макроскопически видимых трещин.
Разница между боковым давлением в твердом каркасе породы и внутренним давлением жидкости на стенках вертикальных трещин, которое в геомеханике именуется эффективным напряжением, определит состояние трещин:
 (4)
(4)
Положительные значения эффективных напряжений определяют возможность формирования хрупких трещин отрыва даже в том случае, когда в твердом каркасе породы действуют сжимающие напряжения. Обратим внимание, что из выражения (4) при υ=0.25 и λ=0.385 (гидростатический закон для флюидного давления) следует, что
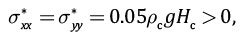 (5)
(5)
т.е. в породе эффективные нормальные напряжения, которые характеризуют состояние в порах и трещинах, являются растягивающими при сжимающих напряжениях в твердом каркасе пород 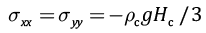 согласно (2).
согласно (2).
Трещины отрыва возникнут в породе, если давление жидкости в трещинах будет больше, чем боковое обжимающее давление в твердом каркасе породы, на величину прочности на отрыв (σt ). В частности, для принятых выше значений флюидного давления (λ=0.385) достижение эффективным горизонтальным напряжением (5) предела прочности на отрыв 7 МПа возникнет при Hc=5400 м. При давлении флюида, приближающемся к литостатическому (λ=0.95), возникновение вертикальных отрывов произойдет на глубине 500–600 м. Большее давление будет приводить к возникновению не только субвертикальных, но и субгоризонтальных трещин отрыва.
4. УСЛОВИЯ ХРУПКОГО РАЗРУШЕНИЯ НА СТАДИИ ДИАГЕНЕЗА
Будем исследовать эволюцию эффективных горизонтальных напряжений в слое осадков как функцию от значения коэффициента Пуассона согласно выражению (4) при постоянном значении всех остальных параметров. На самом деле уменьшение значений этого коэффициента от 0.5, отвечающего высокому насыщению осадков водой, происходит во времени, при этом плотность осадков возрастает (может меняться соотношение λ) и слой постепенно засыпается сверху новыми осадками, что создает дополнительную вертикальную нагрузку.
Поскольку снижение значений коэффициента Пуассона относительно его начального значения, отвечающего высокой водонасыщенности породы, в большей степени связано с физико-химическими процессами, чем с глубиной, на которой находится порода, будем в дальнейшем использовать υ как параметр, определяющий время процесса. Процесс начальной цементации породы происходит достаточно быстро и определяется первыми десятилетиями [Friedman, 1998; Eberli et al., 2003]. За это время порода даже при высокой скорости процесса накопления осадков (например, 1 см/год) в морских отложениях изменяет свою глубину нахождения от морского дна не более чем на 1 м. Это соответствует увеличению вертикальной нагрузки на величину порядка 0.2 кг/см³, поэтому на первом этапе исследований будем пренебрегать влиянием изменения глубины нахождения осадков в процессе начальной стадии диагенеза. Также не будем учитывать изменение соотношения λ в процессе литогенеза.
Как это видно из рис. 2, а, при значении коэффициента Пуассона, близком к 0.36, эффективные горизонтальные напряжения для всего рассмотренного диапазона глубин близки к нулю, а при дальнейшем его уменьшении становятся растягивающими.
Таким образом, без создания деформаций дополнительного горизонтального удлинения из-за наличия флюидного давления в трещинно-поровом пространстве породы и снижения уровня коэффициента Пуассона в процессе диагенеза в слое могут возникнуть условия для формирования хрупких трещин отрыва.
В приведенном выше анализе давление воды в порах считалось подчиняющимся закону гидростатики. Он, скорее всего, действует только на начальной стадии диагенеза, когда υ≈0.5. На этой стадии порода ведет себя как упругая несжимаемая жидкость и поэтому упругие деформации в ней нулевые в любом направлении, εzz=0 (см. также (2)). При снижении уровня значений коэффициента Пуассона в вертикальном направлении появляются упругие деформации укорочения:
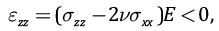 (6)
(6)
где E – модуль упругости Юнга.
Поскольку в процессе начавшегося диагенеза порода будет испытывать упругое уплотнение, сопровождающееся выдавливанием воды из пор, уровень давления воды может превысить гидростатические значения. В связи с этим представленные на рис. 2, а, кривые сместятся вверх, что приведет к появлению положительных значений эффективных горизонтальных напряжений при большем значении коэффициента Пуассона. В частности, если считать, что давление воды в порах превысит гидростатические значения в 1.2–1.5 раза (рис. 3 [Dubinya et al., 2022]), то оно станет больше модуля напряжений горизонтального сжатия в твердом каркасе породы при υ≈0.4 и υ≈0.46 соответственно.
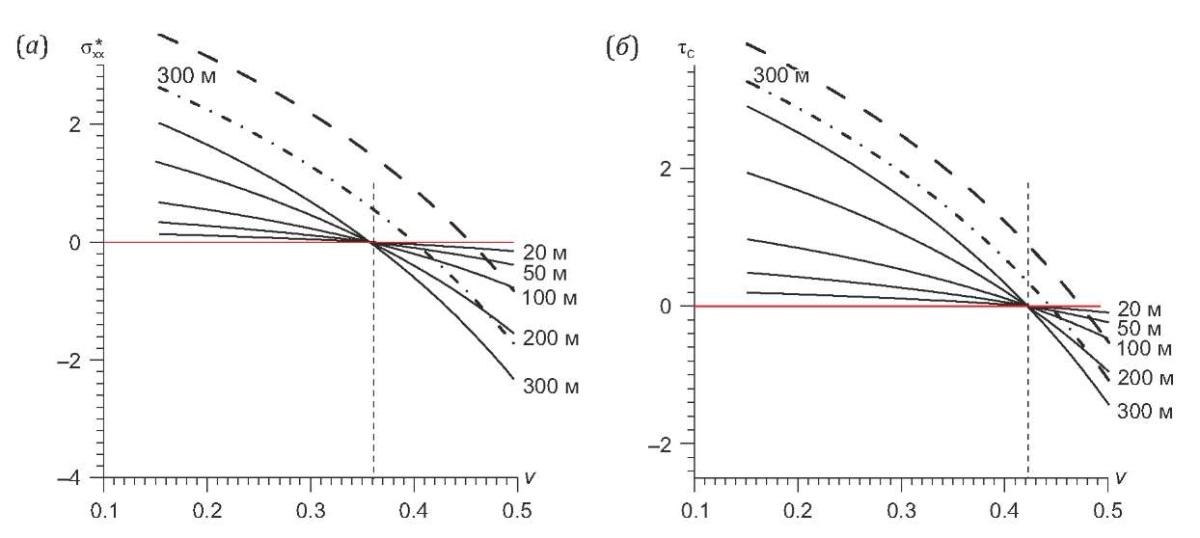
Рис. 2. Зависимость эффективных горизонтальных напряжений (а) и кулоновых напряжений (б) от коэффициента Пуассона для разных глубин расположения слоя (напряжения в МПа), получаемых из выражений (4) и (7) соответственно.
Глубина Hc расположения слоя от морского дна показана рядом с линиями, определяющими значения напряжений. Сплошные линии отвечают λ=0.56, пунктирная и штрихпунктирная линии соответствуют глубине слоя 300 м и λ=0.67 и λ=0.83.
Fig. 2. The change in effective horizontal stresses (a) and Coulomb stresses (б) from the Poisson’s ratio for different depths of the layer arrangement (stresses in MPa) obtained from expressions (4) and (7), respectively.
The depth of the layer from the seabed is shown next to the lines defining the stress values. The solid lines correspond to λ=0.56, and the dotted and dashed lines correspond to the depth of the layer 300 m and λ=0.67 and λ=0.83.
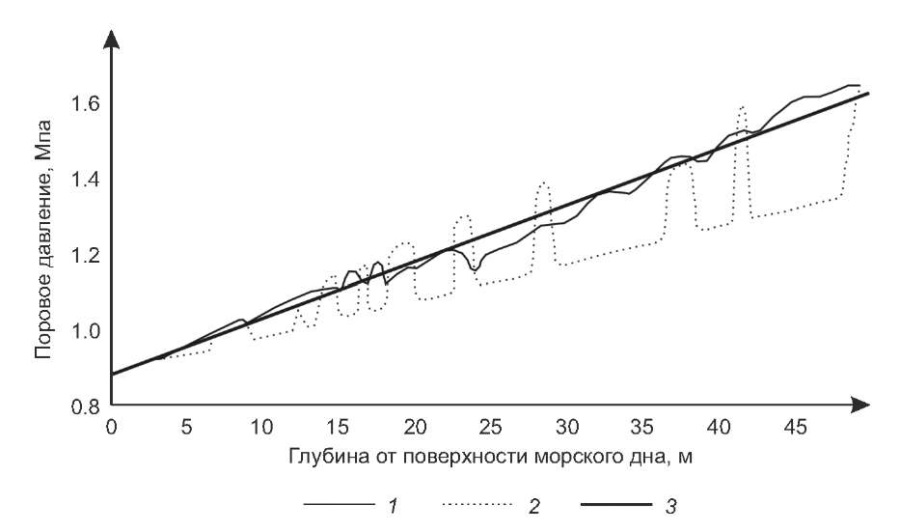
Рис. 3. Изменение давления воды в трещинно-поровом пространстве слабоконосолидированных пород для диапазона глубин Hc 0–50 м, оцененное двумя методами (рисунок из работы [Dubinya et al., 2022], с изменениями).
1 – консолидационный анализ; 2 – моделирование «рок физика»; 3 – прямая линия отвечает флюидному давлению pfl , принятому при расчетах в этой работе.
Fig. 3. Changes of water pressure in the fractured-pore space of weakly consolidated rocks for the depth range Hc from 0–50 m, estimated by two methods (figure from [Dubinya et al., 2022], with changes).
1 – consolidation analysis; 2 – "rock physics" modeling; 3 – straight line corresponds to the fluid pressure pfl used in the calculations in this work.
5. УСЛОВИЯ ПСЕВДОПЛАСТИЧЕСКОГО ТЕЧЕНИЯ И УПЛОТНЕНИЯ ПОРОДЫ
Считаем, что под действием массовых сил из-за изменения механических свойств породы в ней могут развиваться неупругие деформации: псевдопластические (геомеханические) или катакластические (тектонофизические), возникающие за счет микросдвигов, микроотрывов и микросодвигов, и хрупкие за счет объединения микроотрывов в макроотрыв. Поскольку по мере снижения коэффициента Пуассона относительно начального значения (υ=0.5) увеличивается разница между вертикальным и горизонтальным напряжением, это может привести к достижению предела упругости и началу псевдопластического – катакластического течения (ductile flow) породы.
Для анализа возможности псевдопластического течения используем критерий Друккер – Прагера:
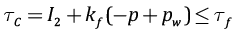 (7)
(7)
при 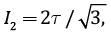
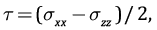
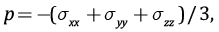
где τC – предельные напряжения, которые далее будем именовать «кулоновыми» напряжениями, I2 – второй инвариант девиатора напряжений, в котором учтено, что σxx=σyy , τf – прочность сцепления (cohesion), kf – коэффициент внутреннего трения (для консолидированных пород он изменяется в диапазоне 0.4–0.8).
Будем так же, как это было сделано в предыдущем разделе, исследовать эволюцию кулоновых напряжений в слое осадков как функцию от значения коэффициента Пуассона согласно выражениям (4) и (7) при постоянном значении всех остальных параметров. Как это видно из рис. 2, б, при значении коэффициента Пуассона, большем 0.42, кулоновы напряжения для всего рассмотренного диапазона глубин отрицательные. Это означает, что для этой стадии процесса диагенеза предел упругости не достигается. При расчетах принималось kf =0.6.
При значении коэффициента Пуассона, меньшем 0.42, порода достигает предела текучести и в ней формируются необратимые псевдопластические деформации за счет смещений по микротрещинам и закрытия пор. Если допустить, что давление воды в порах выше гидростатического, то все линии на графике сместятся вверх и точка достижения предельного состояния сместится вправо, т.е. в область больших значений коэффициента Пуассона.
После достижения предельного состояния в слое активизируются мелкие дефекты прочности в виде микротрещин сдвига, что приводит к интенсификации уплотнения уже за счет необратимых деформаций и более быстрому выдавливанию воды из пор. При этом возникающие на микроуровне необратимые деформации в вертикальном направлении представляют собой укорочение (вертикальное уплотнение породы), а горизонтальные необратимые деформации – удлинение. Боковое стеснение приводит к компенсационному росту упругих деформаций укорочения, что повышает уровень напряжений горизонтального сжатия [Rebetsky, 2008].
Следует отметить, что в выполненных расчетах считалось, что на стадии псевдопластического течения не происходит неупругого изменения объема. Такие изменения могут возникать как за счет формирования новой открытой трещиноватости (дилатансия), так и за счет закрытия пор и ранее существовавшей открытой трещиноватости (компакция) [Stefanov, 2005; Stefanov, Tierselen, 2007]. Также в расчетах не учитывалось увеличение во времени (от коэффициента Пуассона) параметров прочности.
6. НАПРЯЖЕНИЯ В СЛОЕ ПОСЛЕ ДОСТИЖЕНИЯ ПРЕДЕЛЬНОГО СОСТОЯНИЯ
Как это было отмечено в предыдущем разделе, после перехода в закритическое состояние и в начале псевдопластического течения в осадках появляется дополнительное горизонтальное сжатие, которое приводит к изменению закона зависимости полных напряжений горизонтального сжатия от коэффициента Пуассона, показанного на рис. 2, а. Из данных рис. 2, б, видно, что возрастание кулоновых напряжений по мере уменьшения коэффициента Пуассона идет быстрее, чем падение уровня горизонтального сжатия. Это означает, что начало псевдопластического течения (7) слабоцементированных пород (τf ≈0) опережает процесс смены знака эффективных горизонтальных напряжений, следующих из выражения (4), на значение dv≈0.06. Таким образом, по шкале времени (v) начальный этап снижения уровня напряжений горизонтального сжатия из-за уменьшения уровня v, действовавший на стадии упругого состояния, должен смениться этапом повышения горизонтального сжатия – стадия псевдопластического течения. Вопрос состоит в том, в какой момент времени это произойдет. На рис. 4 показаны результаты расчета изменений эффективных напряжений горизонтального сжатия и кулоновых напряжений как функций от коэффициента Пуассона.
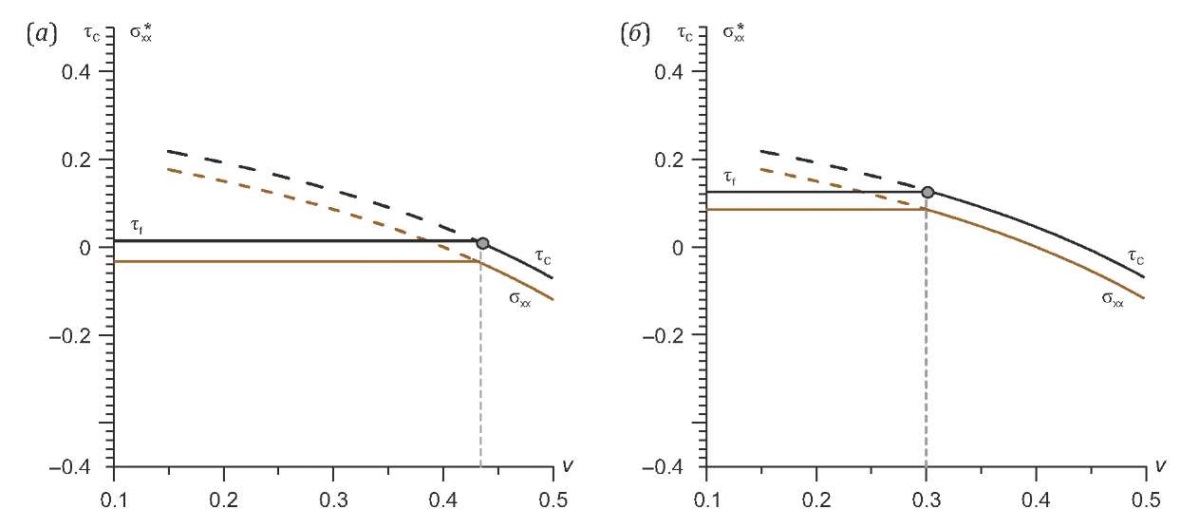
Рис. 4. Схемы, иллюстрирующие изменение уровня эффективных напряжений горизонтального сжатия (линия коричневого цвета) после начала псевдопластического течения в осадочной породе (черная прямая линия – предел сдвиговой прочности породы), для двух разных значений прочности сцепления τf для (а) – пониженная прочность сцепления, для (б) – повышенная прочность сцепления. Кривая линия черного цвета – кулоновы напряжения. Напряжения в МПа. Пунктирные линии – соответствующие напряжения без учета достижения предельного состояния (7). Кружок серого цвета – достижение предельного состояния хрупкой прочности. Расчетные параметры отвечают глубине Hc=20 м.
Fig. 4. Scheme illustrating the change in the level of effective horizontal compression stresses (brown line) after the onset of pseudoplastic flow in a sedimentary rock (black line rock strength limit of shear), for two different values of cohesion strength τf for (a) – reduced adhesion strength, for (б) – increased adhesion strength. The curved line of black color is the Сoulomb stress. Stresses in MPa.Dotted lines are the corresponding stresses without taking into account the achievement of the limit state (7). A gray circle is the achievement of the limit state of brittle strength. The calculated parameters correspond to the depth of Hc=20 m.
Анализ определяющих процесс соотношений (4) и (7) показывает, что в зависимости от уровня прочности сцепления τf начало псевдопластического течения может попадать на стадию, когда эффективные горизонтальные напряжения являются сжимающими или растягивающими (рис. 4). Согласно результатам расчетов после достижения критического состояния (7) уровень горизонтальных напряжений перестает изменяться при уменьшении значения коэффициента Пуассона. Это означает, что дополнительные упругие деформации горизонтального укорочения, возникающие на стадии псевдопластического уплотнения породы, компенсируют дополнительные упругие деформации удлинения, возникающие за счет уменьшения значений коэффициента Пуассона.
Результаты выполненного анализа также показывают, что при низком уровне прочности сцепления на стадии псевдопластического течения (значения коэффициента Пуассона, меньшие 0.43, – левее кружка серого цвета на рис. 4, а) эффективные горизонтальные напряжения отрицательные. Т.е. уровень напряжений горизонтального сжатия в твердом скелете породы больше уровня давления флюида в трещинах. При высоком уровне прочности сцепления на стадии псевдопластического течения (значения коэффициента Пуассона, меньшие 0.3, – левее кружка серого цвета на рис. 4, б) эффективные горизонтальные напряжения положительные. Т.е. уровень напряжений горизонтального сжатия в твердом скелете породы меньше уровня давления флюида в трещинах. Таким образом, в осадочной породе, обладающей меньшей прочностью на скалывание, за счет упругопластического уплотнения возникает более высокий уровень горизонтального сжатия, чем в более прочных породах.
Следует отметить, что при построении схемы рис. 5 не учитывается изменение параметров прочности осадков, которые возрастают во времени. Также не учитывается изменение плотности осадков и уровень водного слоя над морским дном.
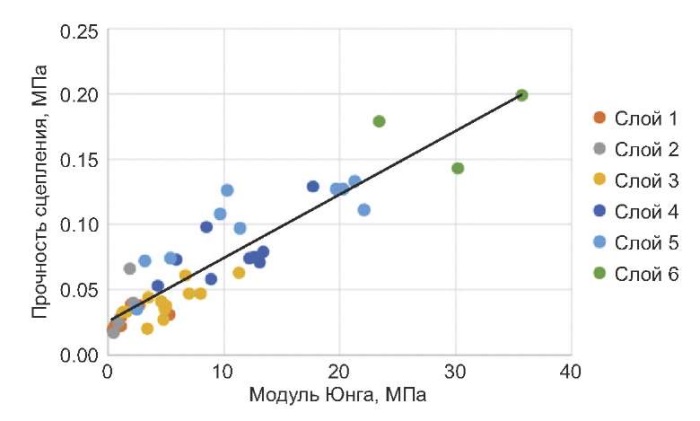
Рис. 5. Прочность сцепления в приповерхностных слоях осадочного бассейна как функция от величины модуля Юнги (МПа) (рисунок из работы [Dubinya et al., 2022]). Черная линия – градиент флюидного давления, принятый в этой работе при расчетах.
Fig. 5. Cohesion strength in the near-surface layers of the sedimentary basin as a function of the value of Young’s modulus (MPa) (a drawing from [Dubinya et al., 2022]). The black line is the fluid pressure gradient used in this work for calculations.
7. МЕХАНИЧЕСКИЕ И ПРОЧНОСТНЫЕ СВОЙСТВА СЛАБОЛИТИФИЦИРОВАННЫХ ОСАДОЧНЫХ ПОРОД
Существуют работы, в которых выполнялась оценка механических и прочностных свойств осадочных слоев на начальной стадии диагенеза. В работе [Dubinya et al., 2022] для осадочных пород на основе сейсмических данных о скорости P- и S-волн, акустического импеданса и плотности в диапазоне глубин от морского дна до 60 м рассчитывались динамические и статические модули упругости, включая объемный модуль и модуль сдвига, модуль Юнга и коэффициент Пуассона. По специальным методикам были также оценены прочность сцепления и коэффициент внутреннего трения (рис. 5).
Средние значения перечисленных выше параметров осадочных слоев представлены в табл. 1.
Таблица 1. Механические свойства и прочностные параметры
в глинистых слоях для глубин до 60 м
Table 1. Mechanical properties and strength parameters
in clay layers for depths up to 60 m
|
Слои |
Описание |
Ht |
Hc |
v |
ρc |
E |
τf |
pfl |
|
EGE 1 |
Мергель |
0.9 |
1.0 |
1.54 |
10 |
0.03 |
0.9 |
|
|
EGE 2 |
Глина |
5.0 |
7.0 |
0.43 |
1.87 |
30 |
0.04 |
1.0 |
|
EGE 3 |
Глина |
6.0 |
7.0 |
0.46 |
1.86 |
60 |
0.04 |
1.0 |
|
EGE 4 |
15.0 |
19.5 |
0.40 |
1.81 |
40 |
0.08 |
1.16 |
|
|
EGE 5 |
19.5 |
33.5 |
0.28 |
1.85 |
70 |
0.10 |
1.35 |
|
|
EGE 6 |
41.0 |
49.5 |
0.31 |
1.90 |
90 |
0.18 |
1.46 |
Примечание. Данные взяты из работы [Dubinya et al., 2022]. Ht – глубина от поверхности морского дна кровли слоя, Hc – средняя глубина от поверхности морского дна кровли слоя, ρc – плотность (г/см³), E – модуль Юнга (МПа), τf – прочность сцепления (МПа), pfl – давление флюида в трещинах (МПа).
Note. The data taken from [Dubinya et al., 2022]. Ht – depth from the seabed surface of the roof layer, Hc – average depth from the seabed surface of the roof layer, ρc – density (g/cm³), E – Young’s modulus (МPа), τf – cohesion strength (МPа), pfl – fluid pressure in fractures (МPа).
Согласно описанию, слои EGE 4–6 отвечают состоянию осадочных пород, прошедших начальную стадию цементации. Будем использовать для этих слоев рассчитанные в работе [Dubinya et al., 2022] параметры, подобрав для них линейную зависимость от глубины (табл. 2):
Y=A+B·Hс. (8)
Таблица 2. Коэффициенты (8) для механических и прочностных параметров
Table 2. Coefficients (8) for mechanical and strength parameters
|
Hс |
ρc (г/см³) |
pfl (МПа) |
v |
τf (МПа) |
kf |
|
B |
0.00288 |
0.012 |
–0.00281 |
0.00337 |
0.00167 |
|
A |
1.75 |
0 |
0.451 |
0.0476 |
0.216 |
Используя данные табл. 2, можно рассчитать изменение напряжений (4) с глубиной без учета достижения критического состояния (7). При расчетах полагаем:
τf =0.0476+0.0337Hc , kf =0.216+0.00167Hc ,
v=0.451–0.00281Hc , ρc=1.75+0.00288Hc , pfl=0.012Hc . (9)
В соотношениях (9) глубина Hc в метрах. Для флюидного давления в сравнении с работой [Dubinya et al., 2022] не учитывается влияние давления морской воды (глубина 90 м).
Из графиков рис. 6 видно, что на глубине около 20 м эффективные горизонтальные напряжения становятся положительными, т.е. давление флюида в трещинах и порах превышает горизонтальное сжатие в твердом скелете породы. Обратим также внимание, что среднее эффективное напряжение (эффективное изотропное давление с обратным знаком) в диапазоне глубин до 40 м сжимающее, но имеет тенденцию на больших глубинах стать растягивающим. Данные прочности на сдвиг осадков в табл. 2 и соотношениях (9) для глубины 40–50 м соответствуют прочности обычных глин.
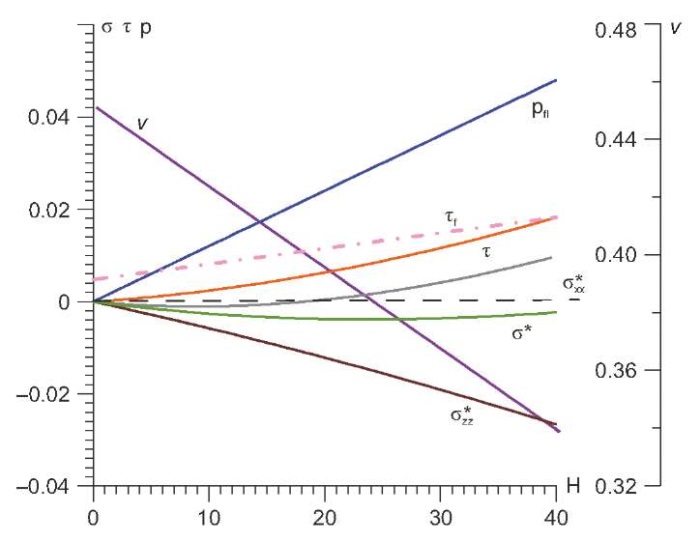
Рис. 6. Эффективные напряжения 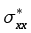 и
и 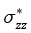 ,
,
максимальное касательное напряжение 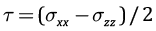 ,
,
эффективное среднее напряжение, 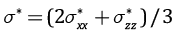 ,
,
давление флюида pfl и прочность сцепления τf (МПа). По горизонтали глубина в метрах.
Fig. 6. Effective stresses 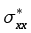 and
and 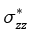 ,
,
maximum shear stress 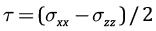 ,
,
effective mean stress 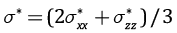 ,
,
fluid pressure pfl and cohesion τf (MPa). Horizontal depth in meters.
Выполним расчеты кулоновых напряжений (7) и эффективных горизонтальных напряжений (4), используя данные (9) для слоев, условно идентифицированных как более прочные породы, например песчаники (рис. 7, а). Другой расчет выполним для некоего слоя, который условно рассматриваем как чисто глиняный (будущие аргиллиты), понизив упругие свойства и плотность относительно данных табл. 2 на 5–10 %. Прочность была понижена на 50 % (рис. 7, б). На рис. 7 также показаны линии предела хрупкой прочности (горизонтальный красный пунктир), возрастающие с глубиной (условные значения). Прочность на отрыв меньше прочности на сдвиг.
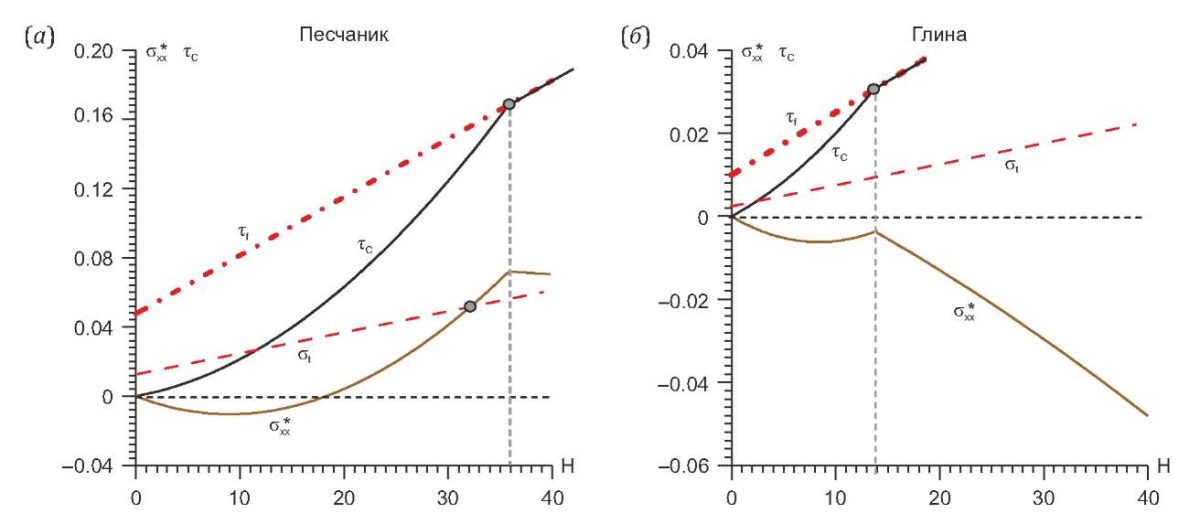
Рис. 7. Схемы, иллюстрирующие зависимость уровня эффективных горизонтальных напряжений и кулоновых напряжений от глубины для двух слоев осадков с разной прочностью сцепления, линейно возрастающей с глубиной. (а) – песчаник; (б) – глины.
Fig. 7. Scheme illustrating the change in the level of effective horizontal stresses and coulomb stresses from depth for two layers of sediments with different adhesion strength, linearly increasing with depth. (a) – sandstone, (б) – shale.
Как это видно из рис. 7, б, для менее прочного слоя (глины) достижение предела прочности на сдвиг (7) произошло на глубине около 14 м при значении коэффициента Пуассона около 0.42 (см. рис. 6). На этой глубине в глине эффективные горизонтальные напряжения были сжимающими. На больших глубинах уплотнение пород начинает происходить более быстро, что повышает уровень эффективных напряжений горизонтального сжатия в сравнении с чисто упругим их поведением (см. рис. 2).
Для более прочного слоя (песчаник) достижение предела прочности на сдвиг (7) произойдет на глубине около 36 м при значении коэффициента Пуассона около 0.355. Эффективные горизонтальные напряжения в этот момент стали уже растягивающими. Если при этом напряжения достигнут уровня предела хрупкой прочности на отрыв σt (на рис. 7, а, это произойдет на глубине около 32.5 м при v=0.36), то в песчанике возникнет две системы взаимно ортогональных субвертикальных отрывов. На рис. 8 показан случай более высокой прочности песчаника. Здесь системы хрупких отрывов не возникает, т.к. на глубине 38 м породы достигают предела упругости и начинается псевдопластическое уплотнение.
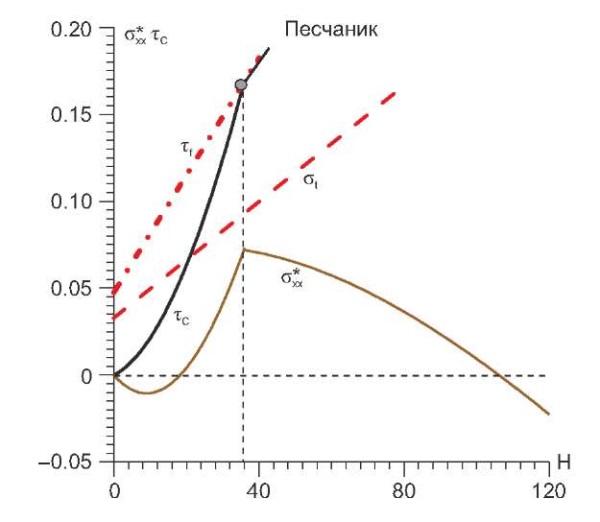
Рис. 8. Схема, иллюстрирующая зависимость уровня эффективных горизонтальных напряжений сжатия и кулоновых напряжений от глубины для песчаника в случае высокой прочности на отрыв.
Fig. 8. Scheme illustrating the change in the level of effective horizontal stresses and coulomb stresses from depth for sandstone in the case of high tensile strength.
После образования отрывов горизонтальные напряжения, действующие в твердом скелете горных пород, станут равными флюидному давлению с обратным знаком 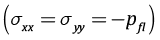 , а эффективное напряжение станет равным нулю.
, а эффективное напряжение станет равным нулю.
Если бы прочность на отрыв в песчанике была больше и растягивающие эффективные горизонтальные напряжения не могли бы достигнуть их значений (рис. 8), то после глубины 36 м растягивающие значения этих напряжений начнут уменьшаться (влияние упругопластического вертикального уплотнения). На глубине около 100 м эффективные горизонтальные напряжения станут сжимающими.
Следует специально заметить, что определяющие соотношения (4) и (7) позволяют реализовать одновременно системы вертикальных отрывов в двух ортогональных направлениях – это самый чистый случай естественного гидроразрыва на стадии литогенеза. Наличие в природном объекте только одной системы субвертикальных отрывов говорит о том, что в осадочных породах кроме напряжений, связанных с действием массовых сил, существовали напряжения локального, регионального или глобального генезиса. Иными словами, в осадочном бассейне в направлении простирания отрывов имело место дополнительное горизонтальное поджатие пласта, либо в направлении, нормальном к отрывам, было дополнительное растяжение пласта. Примером такого дополнительного напряженного состояния является осадконакопление на полого наклоненном склоне – локальные напряжения; напряжения, создаваемые малыми тангенциальными массовыми силами, связанными с неравновесным состоянием формы Земли в поле силы тяжести, – глобальное напряженное состояние [Rebetsky, Myagkov, 2020].
8. ОБСУЖДЕНИЕ
Полученные результаты, с одной стороны, подтверждают гипотезу, высказанную в работах [Hubbert, Willis, 1957; Handin et al., 1963; Secor, 1965], о генезисе систем трещин отрыва как естественном гидроразрыве хрупких пород. С другой стороны, они показывают, что этот гидроразрыв не требует аномально большого флюидного давления и может происходить на малых глубинах в первые десятки метров, а не на глубинах в сотни метров [Chemenda et al., 2021]. Это важно, поскольку показывает, на какой глубине может происходить формирование углеводородного месторождения на начальном этапе.
Исследования автора подкрепляются результатами, представленными в работе [Lavenu, Lamarche, 2018], выполненной по материалам геологических исследований карбонатных отложений Прованс (Юго-Восточная Франция) и Апулийская платформа (Юго-Восточная Италия). В ней было показано, что в обоих районах наблюдалась ранняя стадия трещиноватости, состоящая из субвертикальных трещин отрыва и стилолитов, параллельных залеганию. Эти трещины развивались синхронно на первых этапах захоронения и до крупных тектонических событий. Возникновение и распределение трещин в карбонатах платформенной формы не связано ни с крупномасштабной деформацией, ни с региональной тектоникой.
Проведенные в работе [Lavenu, Lamarche, 2018] исследования позволили установить, что раннее приобретение хрупкости в начале тектогенеза приводит к появлению трещин отрывного типа, развивающихся в плосколежащих породах вдали от складок и разломов. Постепенное упрочнение породы на малых глубинах (0–500 м) делает возможным разрушение при небольших величинах напряжений в очень молодой вмещающей породе (от нескольких лет до нескольких миллионов лет).
Таким образом, теоретические результаты находят свое подтверждение в новых геологических данных о геоморфологии и особенностях развития систем отрывных трещин осадочных бассейнов.
Поскольку процессы литогенеза развиваются достаточно быстро [Friedman, 1998; Eberli et al., 2003] и значимое снижение коэффициента Пуассона и повышение прочности могут происходить за первые сотни лет, региональные тектонические процессы, имеющие, как правило, скорость деформирования 10–7–10–9 1/год (деформация 10–5 за 100 лет), не могут оказать существенное влияние на формирование первичных систем трещин отрыва. В отличие от них, локальные оползневые процессы, происходящие на склоне шельфа, могут играть существенно бóльшую роль в структурировании систем трещин отрыва.
9. ЗАКЛЮЧЕНИЕ
В настоящей работе показано, что формирование ортогональных систем открытых макротрещин (отрывы) осадочных бассейнов может происходить в диапазоне до 100 м глубин шельфа в процессе осадконакопления и цементации. Это явление определяется изменением механических свойств породы в процессе литогенеза. На глубинах в первые десятки метров происходит уплотнение осадков и медленное отжатие излишков воды, определяющее уменьшение коэффициента Пуассона от значений, близких к 0.5, до значений 0.3–0.2. Из-за этого в осадках, напряженное состояние которых практически полностью определяется только силой тяжести вышележащих пород, происходит снижение на 50 % и более уровня напряжений горизонтального сжатия от начального литостатического уровня давления.
На стадии литогенеза в формирующейся породе могут идти два конкурирующих процесса: 1) уменьшение уровня горизонтального сжатия из-за уменьшения значений коэффициента Пуассона; 2) увеличение уровня горизонтального сжатия, обусловленное псевдопластическим течением. Эти два процесса вместе с фактором наличия в трещинах и порах флюидного давления могут приводить к хрупкому разрушению и возникновению систем вертикальных трещин отрыва. Для пород, имеющих низкий уровень предела текучести (глины), упругопластическое уплотнение приводит к повышению уровня напряжений горизонтального сжатия, компенсируя растяжение из-за изменения коэффициента Пуассона. В результате для таких пород хрупкое разрушение становится невозможным. В породах, обладающих высоким уровнем прочности (песчаник, известняк), хрупкое разрушение из-за превышения давления воды в субвертикальных микротрещинах начинается раньше, чем достижение предела сдвиговой текучести.
Таким образом, формирование субвертикальных систем открытых трещин (отрывы) действительно может происходить на стадии диагенеза, при этом их механизм связан не с горизонтальным растяжением осадочной слоистой пачки, а с естественным гидроразрывом пласта, обусловленным превышением разности между напряжением горизонтального сжатия и флюидным давлением в микротрещинах и порах уровня предельных напряжений на отрыв.
Выполненные расчеты показали, что для принятых параметров формирование открытых макроскопически видимых трещин в породах, условно именуемых песчаником, начинает происходить на глубине в 36 м (см. рис. 7, а) и продолжается до глубины около 100 м. Таким образом, весь диапазон глубин развития открытой трещиноватости занимает около 20 м, что при стандартной скорости осадконакопления (0.1–0.3 см/год) соответствует периоду времени около 1000 лет.
Проведенные исследования представляют теоретические основы алгоритма прогноза диапазона глубин развития открытой трещиноватости, а также определяют требуемый набор исходных данных, которые можно использовать для конкретных районов с конкретной структурой осадочных пород.
10. РАСКРЫТИЕ ИНФОРМАЦИИ / DISCLOSURE
Автор заявляет об отсутствии какого-либо конфликта интересов. Автор прочел и одобрил финальную версию перед публикацией.
The author has no conflicts of interest to declare. The author read and approved the final manuscript.
Список литературы
1. Aydin A., 2014. Failure Modes of Shales and Their Implications for Natural and Manmade Fracture Assemblages. AAPG Bulletin 98 (11), 2391–2409. https://doi.org/10.1306/07311413112.
2. Chemenda A.I., 2019. Origin of Regular Networks of Joints: Experimental Constraints, Theoretical Background, and Numerical Modeling. Journal of Geophysical Research: Solid Earth 124 (8), 9164–9181. https://doi.org/10.1029/2019JB017454.
3. Chemenda A.I., Lamarche J., Matonti C., Bazalgette L., Richard P., 2021. Origin of Strong Nonlinear Dependence of Fracture (Joint) Spacing on Bed Thickness in Layered Rocks: Mechanical Analysis and Modeling. Journal of Geophysical Research: Solid Earth 126 (3), e2020JB020656. https://doi.org/10.1029/2020JB020656.
4. Cosgrove J.W., 2001. Hydraulic Fracturing during the Formation and Deformation of a Basin: A Factor in the Dewatering of Low-Permeability Sediments. AAPG Bulletin 85 (4), 737–748. https://doi.org/10.1306/8626C997-173B-11D7-8645000102C1865D.
5. Cumella S.P., Scheevel J., 2008. The Influence of Stratigraphy and Rock Mechanics on Mesaverde Gas Distribution Piceance Basin, Colorado. In: S.P. Cumella, K.W. Shanley, W.K. Camp (Eds), Understanding, Exploring, and Developing Tight-Gas Sands. Proceedings of the Vail Hedberg Conference. AAPG Hedberg Series 3, p. 137–155. https://doi.org/10.1306/13131054H33104.
6. Dinnik A.N., 1926. On Rock Pressure and Calculation of Round Shaft Support. An Engineering Worker 3, 1–12 (in Russian) [Динник А.Н. О давлении горных пород и расчете крепи круглой шахты // Инженерный работник. 1926. № 3. С. 1–12].
7. Dubinya N., Bayuk I., Hortov A., Myatchin K., Pirogova A., Shchuplov P., 2022. Prediction of Overpressure Zones in Marine Sediments Using Rock-Physics and Other Approaches. Journal of Marine Science and Engineering 10 (8), 1127. https://doi.org/10.3390/jmse10081127.
8. Eberli G.P., Baechle G.T., Anselmetti F.S., Incze M.L., 2003. Factors Controlling Elastic Properties in Carbonate Sediments and Rocks. The Leading Edge 22 (7), 654–660. https://doi.org/10.1190/1.1599691.
9. Engelder T., 1985. Loading Paths to Joint Propagation during a Tectonic Cycle: An Example from the Appalachian Plateau, U.S.A. Journal of Structural Geology 7 (3–4), 459–476. https://doi.org/10.1016/0191-8141(85)90049-5.
10. Engelder T., Lacazette A., 1990. Natural Hydraulic Fracturing. In: N. Barton, O. Stephansson (Eds), Rock Joints. A.A. Balkema, Rotterdam, p. 35–43.
11. Epifantsev O.G., Pletenchuk N.S., 2008. Fracturing of Rocks. Fundamentals of Theory and Methods of Study. Siberian State Industrial University, Novokuznetsk, 41 p. (in Russian) [Епифанцев О.Г., Плетенчук Н.С. Трещиноватость горных пород. Основы теории и методы изучения. Новокузнецк: СибГИУ, 2008. 41 с.].
12. Fall A., Eichhubl P., Bodnar R.J., Laubach S.E., Davis J.S., 2015. Natural Hydraulic Fracturing of Tight-Gas Sandstone Reservoirs, Piceance Basin, Colorado. GSA Bulletin 127 (1–2), 61–75. https://doi.org/10.1130/B31021.1.
13. Friedman G.M., 1998. Rapidity of Marine Carbonate Cementation – Implications for Carbonate Diagenesis and Sequence Stratigraphy: Perspective. Sedimentary Geology 119 (1–2), 1–4. https://doi.org/10.1016/S0037-0738(98)00075-X.
14. Frolov V.T., 1992. Lithology. Textbook. Book 1. MSU Publishing House, Moscow, 336 p. (in Russian) [Фролов В.Т. Литология: учебное пособие. М.: Изд-во МГУ, 1992. Кн. 1. 336 с.].
15. Frolov V.T., 1993. Lithology. Textbook. Book 2. MSU Publishing House, Moscow, 432 p. (in Russian) [Фролов В.Т. Литология: учебное пособие. М.: Изд-во МГУ, 1993. Кн. 2. 432 с.].
16. Frolov V.T., 1995. Lithology. Textbook. Book 3. MSU Publishing House, Moscow, 352 p. (in Russian) [Фролов В.Т. Литология: учебное пособие. М.: Изд-во МГУ, 1995. Кн. 3. 352 с.].
17. Guo L., Latham J.-P., Xiang J., 2017. A Numerical Study of Fracture Spacing and Through-Going Fracture Formation in Layered Rocks. International Journal of Solids and Structures 110–111, 44–57. https://doi.org/10.1016/j.ijsolstr.2017.02.004.
18. Handin J., Hager R.V., Friedman M., Feather J.N., 1963. Experimental Deformation of Sedimentary Rocks under Confi Ning Pressure: Pore Pressure Tests. AAPG Bulletin 47 (5), 717–755. https://doi.org/10.1306/BC743A87-16BE-11D7-8645000102C1865D.
19. Hubbert M.K., Willis D.G., 1957. Mechanics of Hydraulic Fracturing. Transactions of the American Institute of Mechanical Engineers 210, 153–168. https://doi.org/10.2118/686-G.
20. Jager J.C., 1962. Elasticity, Fracture and Flow. Springer, Dordrecht, 268 p. https://doi.org/10.1007/978-94-011-6024-7.
21. Lacazette A., Engelder T., 1992. Fluid-Driven Cyclic Propagation of a Joint in the Ithaca Siltstone, Appalachian Basin, New York. International Geophysics 51, 297–324. https://doi.org/10.1016/S0074-6142(08)62827-2.
22. Lavenu A.P.C., Lamarche J., 2018. What Controls Diffuse Fractures in Platform Carbonates? Insights from Provence (France) and Apulia (Italy). Journal of Structural Geology 108, 94–107. https://doi.org/10.1016/j.jsg.2017.05.011.
23. Lorenz J.C., Finley S.J., 1991. Regional Fractures II: Fracturing of Mesaverde Reservoirs in the Piceance Basin, Colorado. AAPG Bulletin 75 (11), 1738–1757. https://doi.org/10.1306/0C9B29ED-1710-11D7-8645000102C1865D.
24. Mandl G., 2005. Rock Joints. The Mechanical Genesis. Springer, Berlin, Heidelberg, 222 p. https://doi.org/10.1007/b137623.
25. Mikhailov A.E., 1956. Field Methods for Studying Cracks in Rocks. Gosgeoltehizdat, Moscow, 132 p. (in Russian) [Михайлов А.Е. Полевые методы изучения трещин в горных породах. М.: Госгеолтехиздат, 1956. 132 c.].
26. Olkhovatenko V.E., Trofimova G.I., Ozhogina T.V., 2015. Methods of Studying Rock Fracturing. Teaching Manual for Independent Work on the Course "Engineering Geology". TSUAB, Tomsk, 80 p. (in Russian) [Ольховатенко В.Е., Трофимова Г.И., Ожогина Т.В. Методы изучения трещиноватости горных пород: Учебно-методическое пособие для самостоятельной работы по курсу «Инженерная геология». Томск: Изд-во ТГАСУ, 2015. 80 с.].
27. Pollard D.D., Aydin A., 1988. Progress in Understanding Jointing over the Past Century. Geological Society of America Bulletin 100 (8), 1181–1204. https://doi.org/10.1130/0016-7606(1988)100%3C1181:PIUJOT%3E2.3.CO;2.
28. Rebetsky Yu.L., 2008. The Mechanism of Generation of Residual Stresses and Large Horizontal Compressive Stresses in the Earth’s Crust of Intraplate Orogens. In: Problems of Tectonophysics. To the 40th Anniversary of M.V. Gzovsky Laboratory of Tectonophysics, IPE RAS. IPE RAS, Moscow, p. 431–466 (in Russian) [Ребецкий Ю.Л. Механизм генерации остаточных напряжений и больших горизонтальных сжимающих напряжений в земной коре внутриплитовых орогенов // Проблемы тектонофизики: К сорокалетию создания М.В. Гзовским лаборатории тектонофизики в ИФЗ РАН. М.: ИФЗ РАН, 2008. С. 431–466].
29. Rebetsky Yu.L., Myagkov D.S., 2020. The Genesis of Tangential Mass Forces in Lithospheric Plates, and Their Role in Geodynamics. Bulletin of Kamchatka Regional Association "Educational-Scientific Center". Earth Sciences 47 (3), 86–97 (in Russian) [Ребецкий Ю.Л., Мягков Д.С. Генезис тангенциальных массовых сил в литосферных плитах и их роль в геодинамике // Вестник КРАУНЦ. Серия: Науки о Земле. 2020. Вып. 47. № 3. С. 86–97]. https://doi.org/10.31431/1816-5524-2020-47-3-86-97.
30. Secor D.T., 1965. Role of Fluid Pressure in Jointing. American Journal of Science 263 (8), 633–646. https://doi.org/10.2475/ajs.263.8.633.
31. Seminsky K.Zh., 2003. Internal Structure of Continental Fault Zones. Tectonophysical Aspect. GEO, Novosibirsk, 244 p. (in Russian) [Семинский К.Ж. Внутренняя структура континентальных разломных зон. Тектонофизический аспект. Новосибирск: Гео, 2003. 244 с.].
32. Spencer C.W., 1987. Hydrocarbon Generation as a Mechanism for Overpressuring in Rocky Mountain Region. AAPG Bulletin 71 (4), 368–388. https://doi.org/10.1306/94886EB6-1704-11D7-8645000102C1865D.
33. Stefanov Yu.P., 2005. Some Features of Numerical Modeling of the Behavior of Elastic-Brittle Plastic Materials. Physical Mesomechanics 8 (3), 129–142 (in Russian) [Стефанов Ю.П. Некоторые особенности численного моделирования поведения упруго-хрупкопластичных материалов // Физическая мезомеханика. 2005. Т. 8. № 3. С. 129–142].
34. Stefanov Yu.P., Tierselen M., 2007. Modeling of the Behavior of Highly Porous Geomaterials at Compaction Band Formation. Physical Mesomechanics 10 (1), 93–106 (in Russian) [Стефанов Ю.П., Тьерселен М. Моделирование поведения высокопористых геоматериалов при формировании полос локализованного уплотнения // Физическая мезомеханика. 2007. Т. 10. № 1. C. 93–106].
35. Strikha V.E., 2012. Methodical Manual on the Discipline "Structural Geology", a Short Course of Lectures. Textbook. Blagoveshchensk, Amur State University, 41 p. (in Russian) [Стриха В.Е. Методическое пособие по дисциплине «Структурная геология», краткий курс лекций: Учебное пособие. Благовещенск: АмГУ, 2012. 41 с.].
36. Price N.J., Cosgrove J.W., 1990. Analysis of Geological Structures. Cambridge University Press, New York, 502 p.
37. Twiss R.J., Moores E.M., 1992. Structural Geology. New York, W.H. Freeman and Company, 532 p.
38. Yurewicz D.A., Bohacs K.M., Yeakel J.D., Kronmueller K., 2003. Source Rock Analysis and Hydrocarbon Generation, Mesaverde Group and Mancos Shale, Northern Piceance Basin, Colorado. In: K.M. Peterson, T.M. Olson, D.S. Anderson (Eds), Piceance Basin Guidebook. Rocky Mountain Association of Geologists, Denver, CO, USA, p. 130–153.
Об авторе
Ю. Л. РебецкийРоссия
123242, Москва, ул. Большая Грузинская, 10, стр. 1
Рецензия
Для цитирования:
Ребецкий Ю.Л. О ВОЗМОЖНОМ МЕХАНИЗМЕ ОБРАЗОВАНИЯ ОТКРЫТОЙ ТРЕЩИНОВАТОСТИ В ОСАДОЧНЫХ БАССЕЙНАХ. Геодинамика и тектонофизика. 2024;15(2):0754. https://doi.org/10.5800/GT-2024-15-2-0754. EDN: GJZCIS
For citation:
Rebetsky Yu.L. ON THE POSSIBLE FORMATION MECHANISM OF THE OPEN FRACTURING IN SEDIMENTARY BASINS. Geodynamics & Tectonophysics. 2024;15(2):0754. (In Russ.) https://doi.org/10.5800/GT-2024-15-2-0754. EDN: GJZCIS



















































