Перейти к:
ВЛИЯНИЕ ОШИБОК ОРИЕНТАЦИИ, СВЯЗАННЫХ С ИСПОЛЬЗОВАНИЕМ МАГНИТНОГО КОМПАСА, НА ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ПАЛЕОМАГНИТНОГО ПОЛЮСА И АМПЛИТУДЫ ДРЕВНИХ ГЕОМАГНИТНЫХ ВАРИАЦИЙ
https://doi.org/10.5800/GT-2024-15-2-0752
EDN: ADJXPH
Аннотация
Использование магнитного компаса при палеомагнитных исследованиях сильномагнитных пород (например, базальтов) может приводить к большим ошибкам ориентации палеомагнитных образцов. В то же время альтернативные методы ориентации относительно времязатратны, а в случае применения солнечного компаса также требуют солнечной погоды – условия, которое далеко не всегда соблюдается, особенно при отборе образцов в высоких и приполярных широтах. Это часто приводит к тому, что исследователи в своей работе все-таки полагаются на результаты измерений магнитным компасом, допуская при этом, что возникающие ошибки носят случайный характер и при достаточно хорошей статистике усредняются. В настоящей работе на примерах, близких к реальным выполнено численное моделирование, которое позволяет проверить это предположение и оценить, насколько ошибки ориентации, связанные с использованием магнитного компаса, могут влиять на конечные результаты палеомагнитных исследований, таких как определение положения палеомагнитного полюса и амплитуды древних геомагнитных вариаций. В результате выполненной работы показано: 1) расчетные величины амплитуд палеовековых вариаций и расчетные положения палеомагнитных полюсов слабочувствительны к умеренным и даже относительно большим ошибкам ориентации палеомагнитных образцов, связанных с применением магнитного компаса; 2) очень большие ошибки ориентации образцов приводят к значительному увеличению внутрисайтового разброса палеомагнитных направлений, что позволяет обнаруживать и отбраковывать соответствующие сайты по большой (например, >15°) величине параметра α95; 3) влияние искажений, связанных с использованием магнитного компаса, на точность определения положения палеомагнитного полюса и амплитуды древних геомагнитных вариаций зависит от широты. На приэкваториальных широтах это влияние максимально, на средних – минимально.
Ключевые слова
Для цитирования:
Ушаков Д.А., Лебедев И.Е., Павлов В.Э. ВЛИЯНИЕ ОШИБОК ОРИЕНТАЦИИ, СВЯЗАННЫХ С ИСПОЛЬЗОВАНИЕМ МАГНИТНОГО КОМПАСА, НА ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ПАЛЕОМАГНИТНОГО ПОЛЮСА И АМПЛИТУДЫ ДРЕВНИХ ГЕОМАГНИТНЫХ ВАРИАЦИЙ. Геодинамика и тектонофизика. 2024;15(2):0752. https://doi.org/10.5800/GT-2024-15-2-0752. EDN: ADJXPH
For citation:
Ushakov D.A., Lebedev I.E., Pavlov V.E. INFLUENCE OF ORIENTATION ERRORS ASSOCIATED WITH THE USE OF A MAGNETIC COMPASS ON THE ACCURACY OF DETERMINING THE POSITION OF THE PALEOMAGNETIC POLE AND THE AMPLITUDE OF PALEOSECULAR VARIATIONS. Geodynamics & Tectonophysics. 2024;15(2):0752. (In Russ.) https://doi.org/10.5800/GT-2024-15-2-0752. EDN: ADJXPH
1. ВВЕДЕНИЕ
Магнитный компас является стандартным устройством, которое используется для ориентации образцов, отбираемых из обнажений горных пород для палеомагнитных исследований. С помощью этого компаса обычно замеряют магнитный азимут и угол падения площадки, по которой выполняется ориентировка образцов, и (в случае необходимости) магнитный азимут падения (или простирания) и угол падения толщи, из которой образцы отбираются. Для того чтобы привести магнитный азимут к истинному, в измеренные значения вносится поправка за склонение, которая может определяться разными способами (например, по модели IGRF [Alken et al., 2021], по топографическим картам, по результатам специальных измерений). Значения этих поправок могут различаться в зависимости от способа их определения, поскольку, например, модели IGRF строятся в значительной степени по данным, которые не учитывают локальные магнитные аномалии, а данные, представленные на топографических картах, с годами устаревают. Практика авторов показывает, что величины такого рода ошибок обычно не превышают 1–2°. Значительно бóльшие ошибки могут возникать под влиянием локальных аномалий магнитного поля, связанных с высокой намагниченностью опробуемых пород. При этом важно отметить, что величина и направление такого аномального поля могут изменяться квазихаотически при переходе от одной точки опробуемого обнажения к другой, что может быть связано с геометрией обнажения, его экспозицией и проч.
В ряде работ [Cromwell et al., 2013; Døssing et al., 2020; и др.] приводятся данные, описывающие величину и характер распределения ошибок ориентации, которые могут возникать при отборе образцов сильномагнитных1 пород с помощью магнитного компаса.
Опыт работ авторов, посвященных изучению вулканических пород Охотско-Чукотского вулканического пояса, показывает, что ошибки при ориентировке образцов магнитным компасом могут достигать нескольких десятков и даже более градусов.
Неудивительно, что среди специалистов широко распространено мнение, что при палеомагнитных исследованиях, связанных с изучением относительно сильно намагниченных пород, в частности базальтов, желательно использовать солнечный компас. Считается (и интуитивно кажется естественным), что это особенно важно при изучении амплитуды древних вековых вариаций (PSV), где точность определения угловых характеристик имеет особое значение.
Вместе с тем обычная альтернативная процедура – ориентация образцов, подразумевающая использование солнечного компаса, связана с некоторыми проблемами. Эта процедура несколько более времязатратна по сравнению с таковой, использующей магнитный компас, но главное – требует солнечной погоды – условия, которое не всегда соблюдается, особенно при отборе образцов в высоких и приполярных широтах. Это часто приводит к тому, что исследователи в своей работе все-таки полагаются на результаты измерений магнитным компасом, допуская при этом, что возникающие ошибки носят случайный характер и при достаточно хорошей статистике усредняются2. Между тем, насколько известно авторам, это мнение никогда численно не проверялось.
Для работы в условиях недостаточного солнечного освещения разработано несколько других в той или иной степени трудоемких методов [Cromwell et al., 2013; Fukuma, Muramatsu, 2022; и др.], один из которых, предполагающий использование теодолита [Lhuillier et al., 2023; Lebedev et al., 2023], был применен в ходе исследований позднемеловых вулканических пород Охотско-Чукотского вулканического пояса.
При этих исследованиях, направленных на изучение вековых геомагнитных вариаций во время Мелового суперхрона нормальной полярности, авторами было изучено около сотни вулканических потоков преимущественно базальтового состава. Выполненные исследования [Lebedev et al., 2022; Lhuillier et al., 2023] позволили сопоставить координаты палеомагнитных полюсов и амплитуды геомагнитных вариаций, полученные по образцам, ориентированным как с помощью магнитного компаса, так и альтернативными методами (с помощью теодолита или солнечного компаса). Результат этого сопоставления оказался поразительным: мало того, что с высокой точностью совпали координаты рассчитанных палеомагнитных полюсов3 (что можно было бы ожидать, принимая во внимание большое число изученных потоков и связанное с этим высокое качество усреднения), с точностью в несколько десятых градуса совпали также значения Sb, параметра, характеризующего разброс виртуальных геомагнитных полюсов (VGP) и используемого для оценки амплитуды древних вековых вариаций [Lebedev et al., 2022; Lhuillier et al., 2023].
Авторами данной статьи предложено объяснение, согласно которому наблюденные совпадения связаны с тем, что исследуемые породы формировались на очень высоких (>80°) палеоширотах. В этих широтах магнитное поле имеет достаточно высокое наклонение, что отражается в очень высоких наклонениях векторов древней намагниченности исследуемых пород, фиксирующей при внедрении и остывании этих пород соответствующее направление магнитного поля. В этой ситуации даже большие ошибки в определении азимута (трансформируемые в ошибки определения склонения вектора древней намагниченности) не ведут к сколько-нибудь значительному изменению направления вектора намагниченности. Например, при максимально возможной ошибке определения азимута, равной 180°, исходное направление вектора D (склонение) = 0°, I (наклонение) = 88° будет определено как направление D (склонение) = 180°, I (наклонение) = 88°, что составит относительно небольшую ошибку определения направления намагниченности, равную 4°.
Следовательно, можно предположить, что существует некоторый интервал палеоширот, для которого нет большой необходимости прибегать к альтернативным методам определения ориентировки палеомагнитных образцов при определении положения палеомагнитных полюсов и амплитуд древних геомагнитных вариаций. Для проверки этого предположения и для оценки ширины этого палеоширотного интервала было выполнено численное моделирование, результаты которого представлены в настоящей статье.
2. МЕТОДЫ ИССЛЕДОВАНИЯ
Выполненное моделирование направлено на сравнение результатов определения амплитуды палеовековых вариаций и положения палеомагнитных полюсов, рассчитанных на основе данных, полученных при использовании магнитного компаса, с такими же результатами, полученными по данным, не искаженным помехами, связанными с применением последнего.
Напомним, что для оценки амплитуд вековых вариаций направления геомагнитного поля геологических эпох, возраст которых превышает сотни тысяч – первые миллионы лет, обычно используют угловой разброс Sb виртуалных VGP, полученных для последовательности независимых по времени вулканических потоков [Cox, 1970; Biggin et al., 2008]. Параметр Sb при этом определяется следующим образом:

где Δi – угловое расстояние i-го VGP, рассчитанное для каждого i-го потока, от среднего VGP (или от географического полюса), N – число потоков и ni – количество проб, взятых из i-го потока, Swi –внутрисайтовая дисперсия VGP, рассчитанная для каждого i-го потока по формуле:
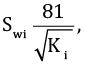
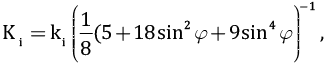
где ki – кучность палеомагнитных направлений внутри i-го сайта, Ki – кучность VGP, рассчитанных для каждого из индивидуальных палеомагнитных направлений внутри i-го сайта, φ – широта сайта.
Для отсечения VGP, связанных с «аномальными» состояниями поля или с грубыми ошибками, используют некоторое пороговое значение – критический угол среза или отсечения (cutoff, ∆max). Виртуальные полюсы, отклоняющиеся от среднего полюса на угол, больший, чем критический (cutoff, ∆max), исключаются, в расчет Sb идут только VGP, отстоящие от среднего полюса на меньший угол. Критическое значение угла ∆max либо выбирают постоянным, например 45° [McElhinny, McFadden, 1997], либо рассчитывают по итеративному методу Вандамма [Vandamme,1994]. В настоящей работе использован ∆max=45°.
Расчет кучностей палеомагнитных направлений, средних палеомагнитных направлений, индивидуальных виртуальных геомагнитных полюсов VGP и средних палеомагнитных полюсов производится по стандартным формулам, представленным, в частности, в работах [Khramov, 1982; Butler, 1992].
В качестве модельного примера используется совокупность из N вулканических потоков (сайтов); из каждого взято по n палеомагнитных образцов. В процессе моделирования сравниваются результаты определения амплитуды древних вековых вариаций и положения палеомагнитных полюсов, рассчитанные по данным обработки палеомагнитных направлений, полученных с использованием для ориентировки образцов либо магнитного компаса, либо альтернативных средств, таких как солнечный компас или теодолит. Принимается, что альтернативные средства позволяют точно ориентировать палеомагнитные образцы, тогда как ориентировка с помощью магнитного компаса дает искаженный результат. Задача моделирования состоит в оценке влияния этого искажения на конечный результат – расчетные значения положения палеомагнитного полюса и амплитуды древних геомагнитных вековых вариаций.
Количество потоков N принималось равным либо 20, либо 60. Первое значение примерно отвечает количеству потоков, минимально необходимому для корректной оценки палеовековых вариаций [Biggin et al., 2008], второе значение – числу потоков, обеспечивающему, по принятому мнению, достаточную статистическую базу для такой оценки.
Число направлений (образцов) n=12 выбиралось исходя из практики палеомагнитных исследований авторов, которая, впрочем, вполне соответствует, мировой. Значения кучности, которые использовались при фишеровском моделировании направлений внутри сайтов (потоков), также выбирались на основе практики подобных исследований от «относительно неплохой» кучности (K=25) до «хорошей» (K=100) и «очень хорошей» (K=200).
Для внесения помехи в неискаженные данные авторами была выполнена аппроксимация нормальным распределением реального распределения ошибок, определенных в ходе последних исследований вулканических пород Охотско-Чукотского вулканического пояса [Lebedev et al., 2023] (рис. 1). Это распределение имеет среднее значение, близкое к 0, и стандартное отклонение σ=17°. Следует отметить, что подобные реальные распределения ошибок, связанных с использованием магнитного компаса, можно найти также в работах [Cromwell et al., 2013; Døssing et al., 2020]. Довольно большое значение стандартного отклонения в рассмотренном реальном распределении ошибок обусловлено наличием некоторого числа образцов (5–6 % от всей коллекции), ориентировки которых определены с очень большой (несколько десятков градусов) ошибкой. Этого можно, избежать, исключая при отборе участки обнажений, явным образом влияющие на положение магнитной стрелки компаса. В таком случае стандартное отклонение существенно уменьшается [Døssing et al., 2020] до 6–8° и меньше, поэтому, при моделировании авторы решили рассматривать три варианта возможных помех: умеренные (σ=8°), большие (σ=17°) и очень большие (σ=34°).

Рис. 1. Распределение ошибок склонений при использовании магнитного компаса (по результатам палеомагнитных исследований вулканических пород Охотско-Чукотского пояса [Lebedev et al., 2022; Lhuillier et al., 2023]): (а) – для индивидуальных образцов, (б) – для средних склонений по сайтам.
Fig. 1. Distribution of declination errors when using a magnetic compass (based on the results of paleomagnetic studies of volcanic rocks of the Okhotsk-Chukchi belt [Lebedev et al., 2022; Lhuillier et al., 2023]): (а) – individual samples, (б) – site means.
Моделирование выполнялось по следующему алгоритму (рис. 2):
1. Для каждого из N модельных вулканических потоков (сайтов), расположенных в точке с координатами φ=0° и λ=0° (где φ и λ – широта и долгота соответственно), с использованием модели TK03 [Tauxe, Kent, 2004] и программы из пакета [Tauxe et al., 2016] генерировались единичные векторы с направлениями Di , Ii , которые принимались за направление геомагнитного поля во время формирования данного потока (сайта).
2. Вокруг этих направлений для каждого индивидуального сайта, также с помощью программ из пакета [Tauxe et al., 2016], моделировалось фишеровское распределение из n=12 векторов, каждое из которых отвечает модельному палеомагнитному направлению индивидуального модельного палеомагнитного образца. Полученные N распределений по 12 векторам рассматривались в качестве исходных ненарушенных («истинных») распределений, не испытавших помех, связанных с использованием магнитного компаса.
3. В исходные N распределений палеомагнитных направлений вносилась помеха (искажение, шум), связанная с использованием магнитного компаса. Используя нормальные распределения с нулевым средним значением и со стандартными отклонениями σ=8° (17°, 34°), авторы получали случайное угловое значение для каждого индивидуального палеомагнитного образца (направления), которое добавлялось к склонению исходного направления. В результате для каждого из N сайтов были получены искаженные распределения, каждое из которых включало по 12 искаженных палеомагнитных направлений.
4. Для каждого из N сайтов по полученным распределениям 12 «истинных» и «искаженных» векторов рассчитывались средние направления, кучности (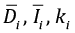 ) и соответствующие VGP. На основе этих данных определялись «истинные» и «искаженные» VGP для индивидуальных сайтов, а затем для совокупности N сайтов рассчитывались «истинные» и «искаженные» параметры Sb и координаты среднего VGP (палеомагнитного полюса).
) и соответствующие VGP. На основе этих данных определялись «истинные» и «искаженные» VGP для индивидуальных сайтов, а затем для совокупности N сайтов рассчитывались «истинные» и «искаженные» параметры Sb и координаты среднего VGP (палеомагнитного полюса).
Затем для той же совокупности вычислялись ошибки определения положения среднего полюса δVGP.
Эта процедура (п. 1–5) повторялась 1000 раз, после чего определялись средние значения δVGP и Sb и их доверительные 95%-ные интервалы.
Вычисления (1) – (6) повторялись для разных широт из интервала 0–90° с шагом 10°, в результате чего определялись широтные зависимости δVGP и Sb и их доверительных интервалов.

Рис. 2. Схема, иллюстрирующая алгоритм выполненного моделирования.
Fig. 2. Flow chart illustrating the algorithm of the performed simulation.
3. РЕЗУЛЬТАТЫ
Авторы сравнивают массивы искаженных и неискаженных данных (рис. 3, 4), каждый из которых включает N направлений (N=60, 20). Каждое из этих N направлений является средним направлением, рассчитанным для индивидуального сайта. Каждому индивидуальному сайту соответствуют 12 искаженных и 12 неискаженных направлений (рис. 3, 4), отвечающих индивидуальным модельным образцам. Конечной целью исследования является выяснение влияния вносимых искажений на конечный результат (т.е. на параметр Sb и положение палеомагнитного полюса).

Рис. 3. Примеры моделирования направлений в индивидуальных сайтах и влияния вносимых искажений на эти направления. Левый, центральный и правый столбцы – три различных примера, 1-я строка – неискаженные данные, 2, 3 и 4-я строки соответственно – данные с внесенными умеренными, сильными и очень сильными искажениями (отвечающими стандартному отклонению 8, 17 и 34°). Моделирование проводилось для широты 5°.
Fig. 3. Examples of modeling directions in individual sites and the impact of introduced distortions on these directions. The left, center and right columns are three different examples, the 1st row is undistorted data, the 2nd, 3rd and 4th columns, respectively, are data with moderate, strong and very strong distortions (corresponding to standard deviation 8, 17 and 34°). The simulation was carried out for latitude 5°.

Рис. 4. Примеры моделирования совокупностей из средних направлений 60 модельных сайтов и влияния на них вносимых искажений. Левый, центральный и правый столбцы – три различных примера, 1-я строка – неискаженные данные, 2, 3 и 4-я строки соответственно – данные с внесенными умеренными, сильными и очень сильными искажениями (отвечающими стандартному отклонению 8, 17 и 34°). Моделирование проводилось для широты 5°.
Fig. 4. Examples of modeling sets from the average directions of 60 model sites and the impact of introduced distortions on them. The left, center and right columns are three different examples, the 1st row is undistorted data, the 2nd, 3rd and 4th columns, respectively, are data with moderate, strong and very strong distortions (corresponding to standard deviation 8, 17 and 34°). The simulation was carried out for latitude 5°.
Прежде чем перейти непосредственно к изложению результатов моделирования, нужно выполнить проверку разработанной авторами программы. Такую проверку можно выполнить путем сравнения результатов вычисления широтных зависимостей Sb, кучностей палеомагнитных направлений и VGP, рассчитанных из модели ТК03 авторами и их коллегами ранее. Из рис. 5 видно, что данные авторов (с учетом их статистической природы) согласуются с результатами расчетов, представленных в работе [Deenen et al., 2011]. Таким образом, программа авторов успешно проходит тестирование.
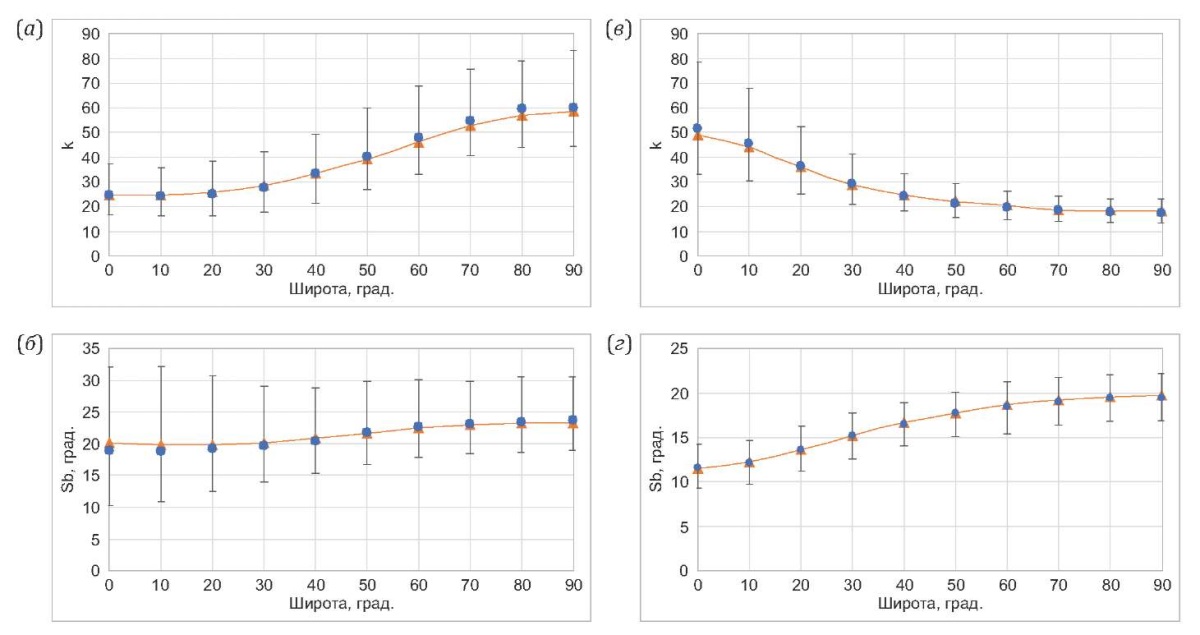
Рис. 5. Сравнение результатов расчета широтных зависимостей параметра Sb, кучности VGP (K) и кучности палеомагнитных направлений (k), полученных из модели ТК03 в данной работе и в работе [Deenen et al., 2011].
(а) – сравнение широтных зависимостей кучности палеомагнитных направлений; (б) – сравнение широтных зависимостей Sb без применения cutoff; (в) – сравнение широтных зависимостей кучностей VGP без применения cutoff; (г) – сравнение широтных зависимостей Sb с применением cutoff. Оранжевыми треугольниками и аппроксимирующей их оранжевой линией показаны данные, взятые из работы [Deenen et al., 2011], синими кружками (и соответствующими вертикальными линиями) показаны величины, рассчитанные в настоящей работе (и их интервалы 95%-ного доверия). Расчеты в работе [Deenen et al, 2011] производились на основе моделирования для каждой широты 10 тыс. палеомагнитных направлений. В данной работе соответствующие величины вычислялись путем осреднения тысячекратного моделирования 60 точек (см. описание алгоритма в тексте).
Fig. 5. Comparison of the results of calculating Sb, VGP precision parameter and paleomagnetic directions precision parameter obtained from the TK03 model in this paper and [Deenen et al., 2011].
(a) – comparison of latitudinal dependences of paleomagnetic directions accuracy; (б) – comparison of latitudinal dependences of without t cutoff; (в) – comparison of latitudinal dependences of VGP accuracy; (г) – comparison of latitude dependencies of Sb with cutoff. The orange triangles and their approximate orange line show the data taken from [Deenen et al., 2011], the blue circles (and the corresponding vertical lines) show the values calculated in this work (and their 95 % confidence intervals). Calculations in [Deenen et al, 2011] were based on modeling for each latitude of 10000 paleomagnetic directions. In this study, the corresponding values were calculated by averaging a thousandfold simulation of 60 points (see the description of the algorithm in the text).
Влияние погрешностей, связанных с ориентацией палеомагнитных образцов с помощью магнитного компаса, на расчетные значения амплитуды древних вековых вариаций. На рис. 6 представлены результаты, демонстрирующие влияние погрешностей, связанных с ориентацией палеомагнитных образцов с помощью магнитного компаса, на расчетные значения амплитуды древних вековых вариаций Sb. В данном примере в качестве исходного неискаженного распределения палеомагнитных направлений внутри сайтов использовалось фишеровское распределение двенадцати направлений с кучностью 25, а уровень искажения сигнала изменялся от умеренного (σ=8°) до сильного (σ=17°) и очень сильного (σ=34°). Рассмотрены случаи, когда внутрисайтовый разброс Swi не учитывался (рис. 6, а, д, и), учитывался (рис. 6, б, е, к) и когда вместе с учетом внутрисайтового разброса Swi проводилось также отсечение сайтов по значению параметра α95 – 95%-ному углу доверия в фишеровской статистике (рис. 6, в, ж). В качестве критического угла отсечения выбирался угол 15° – сайты с большим значением этого угла в расчете Sb не учитывались. Эта процедура часто используется при обработке данных палеомагнитных исследований, и интересно посмотреть, как она может влиять на конечный результат. Во всех случаях применялось отсечение тех VGP, которые отклонялись от среднего на угол, больший ∆max=45°.
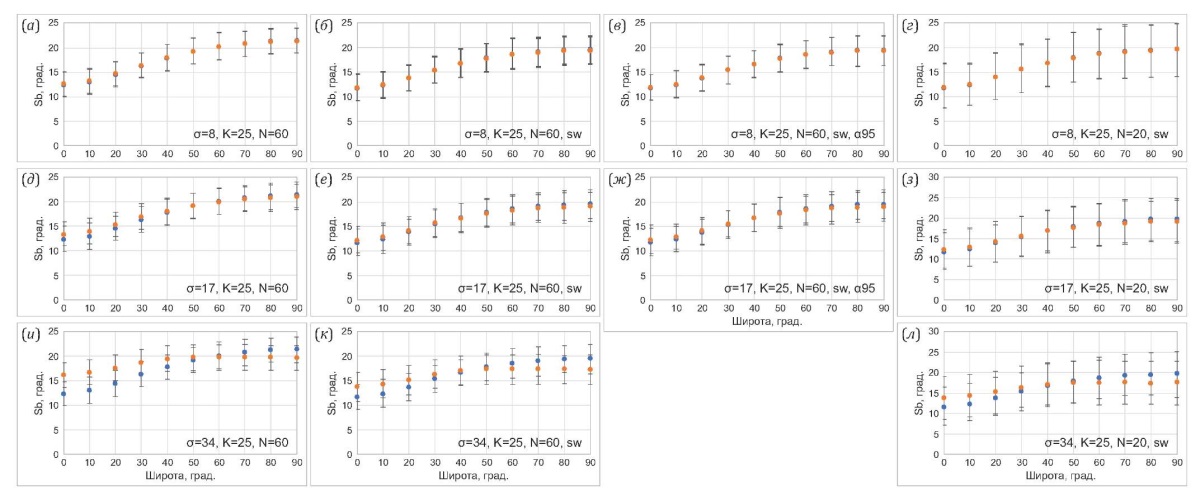
Рис. 6. Сравнение широтных зависимостей для «искаженных» и для «неискаженных» данных.
Голубые кружки и соответствующие им вертикальные линии показывают значения Sb и их 95 %-ные доверительные интервалы, рассчитанные по «неискаженным» данным. Оранжевые кружки и соответствующие вертикальные линии показывают значения Sb и их 95%-ные доверительные интервалы, рассчитанные по «искаженным» данным. σ – величина стандартного отклонения в нормальном распределении, использованном для моделирования искажений (σ=8° – умеренные искажения; σ=17° – сильные искажения; σ=34° – очень сильные искажения); K – кучности внутрисайтовых распределений; N – число модельных вулканических потоков (сайтов); символы sw означают, что при расчете учитывался внутрисайтовый разброс; символы α95 означают, что выполнялась селекция сайтов по величине α95 (см. пояснения в тексте).
Fig. 6. Comparison of Sb latitude dependencies for "distorted" and for "undistorted" data.
The blue circles and their corresponding vertical lines show the Sb values and their 95 % confidence intervals calculated from "undistorted" data. Orange circles and corresponding vertical lines show values and their 95 % confidence intervals calculated from "distorted" data. σ – value of the standard deviation in the normal distribution used to model distortions (σ=8° – moderate distortions; σ=17° – strong distortions; σ=34° – very strong distortions); K – accuracy of intra-site distributions; N – number of model volcanic flows (sites); sw symbols mean that the calculation took into account the in-site spread; α95 symbols mean that the selection of sites by the value of α95 was carried out (see explanations in the text).
Как видно из рис. 6, а, при умеренных искажениях значения Sb, рассчитанные по искаженным данным для всех широт, практически не отличаются от «истинных» Sb, и этот вывод не зависит от учета или неучета внутрисайтового разброса и от применения селекции по углу α95 (рис. 6, б, в).
Некоторые следы такого различия появляются при введении сильных искажений (рис. 6, д–ж), и только при введении очень сильных искажений начинает явно проявляться систематическое различие между средними значениями искаженных и «истинных» Sb (рис. 6, и–л). Широтное соотношение между этими параметрами следующее. На экваторе и в низких широтах среднее значение искаженного Sb заметно (на 4–6°) выше «истинного» Sb При увеличении широты значения этих параметров сходятся и вблизи 40–50° широты они практически не различаются. Далее при увеличении широты искаженный параметр Sb становится все меньше «истинного» и вблизи полюса их различие может составлять 2–3° (рис. 6, и–л). При ближайшем рассмотрении широтных зависимостей Sb, искаженных шумами умеренного и сильного уровня, проявляется та же закономерность, но масштаб ее значительно меньше, чем при очень сильных шумах.
На рис. 7 показано сравнение широтных кривых «истинной» и искаженной величины Sb в зависимости от значения кучности исходных распределений палеомагнитных направлений внутри сайтов. Как видно из этого сравнения, изменение кучности в интервале значений 25–200 практически не влияет на соотношение этих кривых.
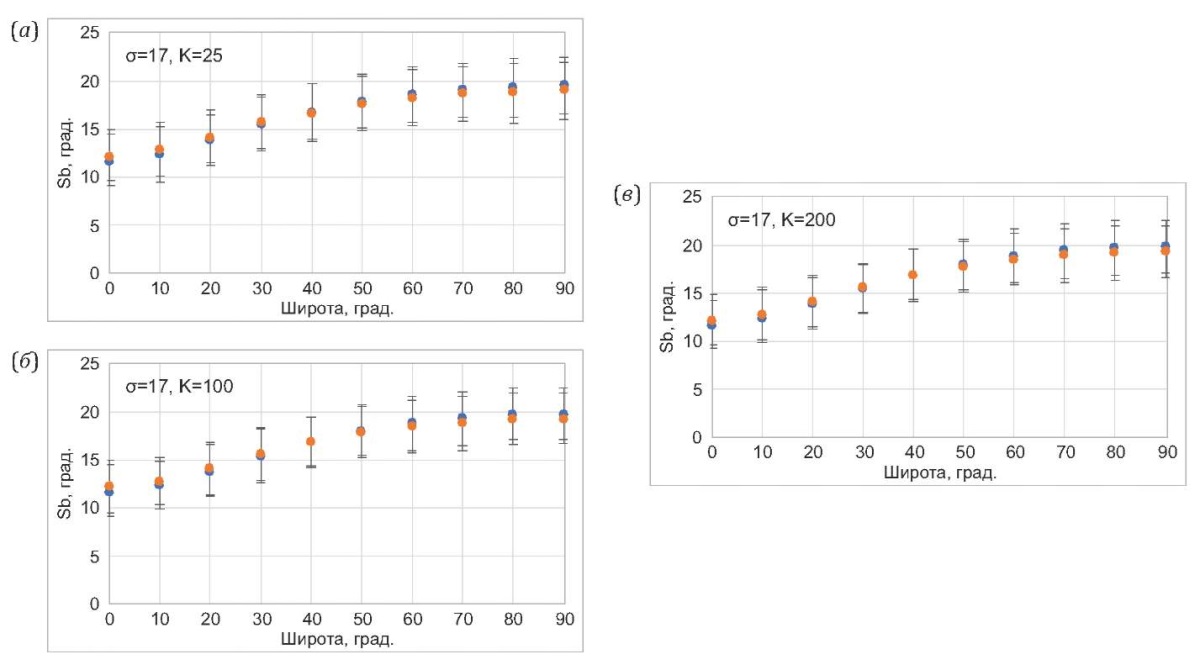
Рис. 7. Влияние внутрисайтовой кучности на широтные зависимости расчетных Sb
для «искаженных» и «неискаженных» данных. Обозначения те же, что на рис. 5.
Fig. 7. The effect of in-site precision on the latitude dependences of calculated Sb
for "distorted" and "undistorted" data. The captions are the same as in Fig. 5.
Далеко не во всех исследованиях, направленных на определение амплитуды древних геомагнитных вариаций по палеомагнитной записи, содержащейся в вулканических потоках, удается изучить 60 и более вулканических потоков. В связи с этим важно понимать, как на соотношение искаженных и «истинных» Sb будет влиять уменьшение числа опробуемых потоков. На рис. 6, г, з, м, показаны соответствующие широтные зависимости, рассчитанные для числа потоков, равного 20. Как видно из рис. 6, даже при таком существенном уменьшении числа исследуемых потоков среднее значение искаженного Sb незначительно отличается от среднего значения «истинного» Sb, однако доверительный интервал заметно расширяется по сравнению с аналогичными интервалами, рассчитанными для N=60.
Влияние погрешностей, связанных с ориентацией палеомагнитных образцов с помощью магнитного компаса, на ошибку определения палеомагнитного полюса. Угловые расстояния между «истинным» и искаженным положением палеомагнитного полюса рассчитаны для разного уровня шумов (σ=8, 17, 34°), для разного числа потоков (N=20, 60) и для разных значений кучностей исходных направлений внутри сайтов. Все вычисления выполнялись с использованием угла отсечения ∆max=45°, отдельно рассматривалось влияние отбраковки данных по сайтам, характеризующимся величиной α95>15°. Результаты выполненных расчетов показаны на рис. 8.
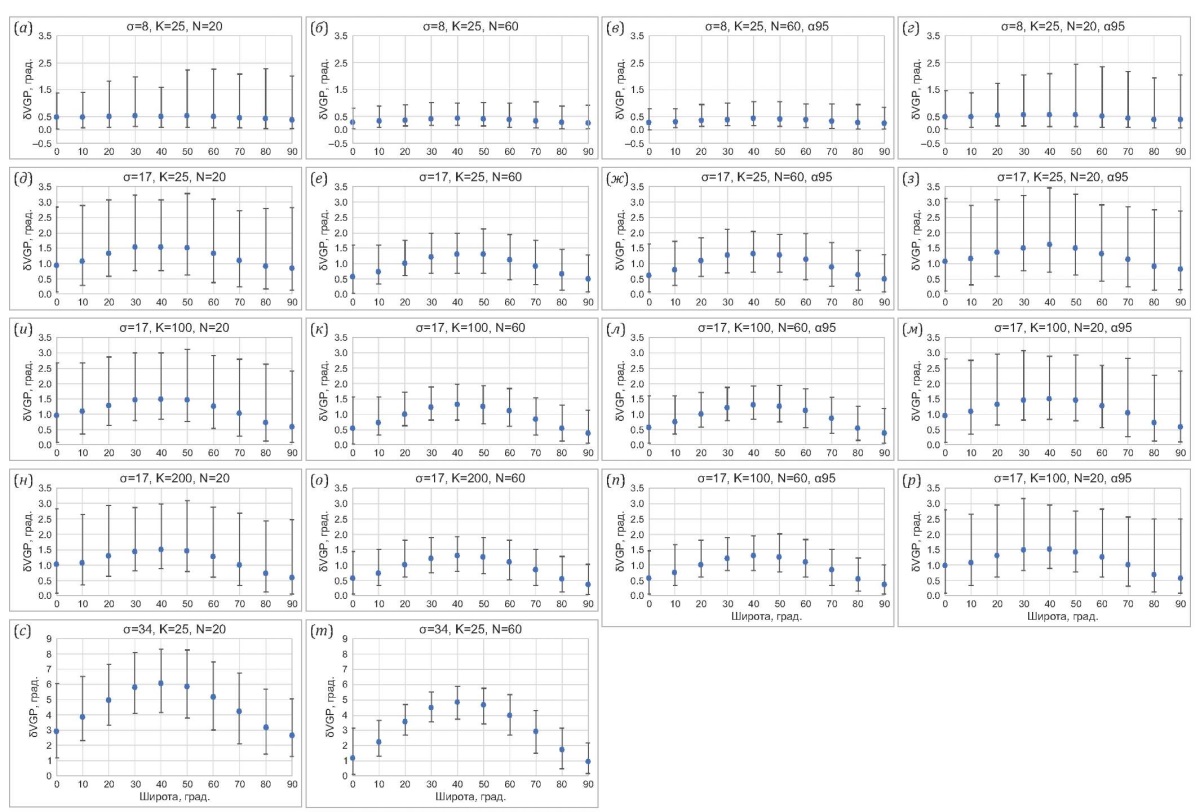
Рис. 8. Ошибка определения положения палеомагнитного полюса (δVGP). Угловые отличия (и соответствующие доверительные интервалы) палеомагнитных полюсов, рассчитанных на основе «искаженных» и «неискаженных» данных.
Fig. 8. Discrepancies in determining the position of the paleomagnetic pole (δVGP). Angular differences (and corresponding confidence intervals) of paleomagnetic poles calculated from "distorted" and "undistorted" data.
Во втором столбце этого рисунка представлены графики, показывающие отклонения искаженного полюса от «истинного» при N=60. Видно, что это отклонение при умеренном уровне помех (σ=8°) для всех широт не превышает 0.5° (рис. 8, б). При больших помехах (σ=17°) расхождение «истинного» и «искаженного» полюсов возрастает и достигает максимума на сороковой широте, не превышая при этом 1.5° (рис. 8, е). Дальнейшее увеличение уровня помех приводит к еще большему расхождению рассматриваемых полюсов: при σ=34° при том же характере широтной зависимости это расхождение становится равным ~6° (рис. 8, т).
Селекция сайтов по величине α95 не приводит к каким-либо существенным изменениям (рис. 8, в, ж). Разница состоит только в том, что при очень большом уровне помех рассчитать отклонение «искаженного полюса» от «истинного» становится невозможно, поскольку наложенное условие (α95>15°) исключает, как правило, в этом случае все «искаженные» сайты из расчета.
Уменьшение числа потоков до 20 приводит к крайне небольшому увеличению рассматриваемого среднего отклонения, при этом, однако, доверительные интервалы существенно возрастают (рис. 8, а, д, с, г, з).
Расчеты авторов показывают, что изменение внутрисайтовой кучности от 25 до 200 практически не отражается на величине ошибки определения положения полюса (рис. 8, и–р).
4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Результаты расчетов существенно отличаются от ожидавшихся авторами статьи. Исходное предположение авторов состояло в том, что различия «истинных» и искаженных параметров Sb будут значительны и максимальны на экваторе и будут уменьшаться (возможно, становясь незначительными) при приближении к полюсу. Выполненное моделирование рисует другую картину.
Действительно, на экваторе эти различия максимальны, однако при умеренном и сильном уровне помех их величина крайне мала и не превышает 1°, т.е. существенно меньше погрешностей, характерных при определении значений Sb при исследовании природных объектов (например [Doubrovine et al., 2019]). На широтах 40–50° внесение умеренных и больших искажений в исходный сигнал практически не приводит к изменению конечного результата, а при дальнейшем движении к полюсу можно наблюдать кажущийся парадоксальным результат: введение искажений не увеличивает, а, наоборот, уменьшает величину Sb, т.е. разброс виртуальных геомагнитных полюсов VGP. Несмотря на то, что эта тенденция ярко проявляется только при очень большом уровне шумов (σ=34°), а при умеренных и больших шумах она не очень заметна и не связана с большими изменениями расчетного параметра Sb, сам факт ее существования требует объяснения.
При увеличении степени искажений увеличивается разброс направлений внутри сайтов (см. рис. 3, 4; рис. 9, а, б), соответственно увеличивается и величина Swi, которая входит со знаком минус в формулу расчета Sb, поэтому естественно предположить, что уменьшение Sb связано именно с этим эффектом (непонятно, впрочем, почему этот эффект мог бы иметь широтную зависимость). Для проверки этого предположения можно сравнить широтные зависимости значений Sb, рассчитанных с учетом и без учета внутрисайтового разброса. Из сравнения фрагментов рис. 6, и, и рис. 6, к, видно, что обсуждаемая тенденция наблюдается и в случае неучета внутрисайтового разброса (см. рис. 6, и), следовательно, необходимо искать другое объяснение.

Рис. 9. Эффект увеличения кучности среднесайтовых направлений на высоких широтах
при внесении искажений, связанных с использованием магнитного компаса.
(а, б) – характер изменения распределений исходных направлений после внесения в них искажений, моделирующих ошибку ориентировки образцов, отобранных с помощью магнитного компаса в двух сайтах на широте 70°. В каждой паре (левой (первый сайт) и правой (второй сайт)) слева – исходные направления, справа – искаженные направления. (в) – схема, иллюстрирующая увеличение кучности распределения средних направлений по сайтам при внесении искажений, моделирующих ошибку ориентировки образцов, отобранных с помощью магнитного компаса. Внешние белые круги обозначают исходное круговое распределение палеомагнитных направлений внутри сайтов; внутренние белые круги – неискаженные средние направления распределений палеомагнитных направлений внутри сайтов; серые полукруги показывают характер изменения внутрисайтовых распределений после внесения искажений; черные круги – средние направления распределения палеомагнитных направлений внутри сайтов после их искажения; стрелки показывают изменение средних внутрисайтовых направлений после внесения искажений. (г) – широтные зависимости кучности искаженных (оранжевые кружки) и неискаженных (синие кружки) среднесайтовых направлений. Рассчитано для кучности внутрисайтовых направлений K=25, для очень сильных искажений σ=34° и для числа сайтов (потоков) N=60.
Fig. 9. Convergence of the site-mean directions
due to distortion of the declinations of the samples.
(а, б) – the nature of the change in the distributions of the initial directions after introducing distortions into them, modeling the orientation error of samples taken using a magnetic compass at two sites at latitude 70°. In each pair (left (first site) and right (second site)) on the left – the original directions, on the right - the distorted directions. (в) – a diagram illustrating an increase in the accuracy of the distribution of average directions across sites when distortions are introduced that simulate the orientation error of samples taken using a magnetic compass. The outer white circles indicate the initial circular distribution of paleomagnetic directions inside the sites; the inner white circles – undistorted average directions of paleomagnetic directions distributions inside the sites; gray semicircles show the nature of changes in the intra-site distributions after the introduction of distortions; black circles represent the average distribution directions of paleomagnetic directions within sites after their distortion; arrows show the change in average intra–site directions after the introduction of distortions. (г) – latitudinal dependences of the accuracy of distorted (orange circles) and undistorted (blue circles) mid-byte directions. Calculated for the accuracy of precision parameter k=25, for very strong distortions σ=34° and for the number of sites (streams) N=60.
Представляется, что такое объяснение кроется в характере изменения формы исходных распределений палеомагнитных направлений при внесении искажений и в широтной зависимости влияния этих изменений на конечный результат. Независимо от широты, ошибки, связанные с влиянием на магнитный компас сильнонамагниченных пород, изменяют только склонения рассматриваемых векторов, а не их наклонения. Это приводит к «растаскиванию» исходных фишеровских (т.е. обладающих круговой симметрией) распределений по склонению, что порождает тенденцию к формированию бананообразных распределений (рис. 9, а–в; см. рис. 3). В то время как на низких широтах этот эффект практически никак не влияет на кучность среднесайтовых направлений, на высоких и очень высоких широтах формирование бананообразных распределений приводит к тому, что среднесайтовые направления искаженных распределений приобретают большие наклонения, сближаются и это приводит к усилению их группирования по сравнению с неискаженными среднесайтовыми направлениями (рис. 9, в). Кучность распределения искаженных среднесайтовых направлений растет (рис. 9, г), соответственно разброс VGP уменьшается.
Разумеется, возмущающее действие вносимых искажений никуда не исчезает, и можно наблюдать взаимодействие двух разнонаправленных эффектов: увеличения разброса полюсов за счет вносимых искажений и уменьшения разброса полюсов за счет образования бананообразной формы распределений направлений. На низких широтах преобладает первый эффект, на средних широтах их действие уравновешивается, на высоких широтах преобладает второй эффект.
Выполненное численное моделирование приводит к удивительному выводу: расчетные величины амплитуды палеовековых вариаций и положения палеомагнитного полюса оказываются слабочувствительны к умеренным и даже относительно большим ошибкам ориентации палеомагнитных образцов, связанных с применением магнитного компаса. Это, в первую очередь, относится к средним значениям Sb и средним положениям палеомагнитных полюсов, рассчитанным по результатам 1000 испытаний. Однако при изучении природных объектов исследователь имеет дело не с 1000 совокупностей вулканических потоков, а, как правило, только с одной, поэтому для практического применения такого вывода важно представлять границы доверительных интервалов этих средних значений.
Выполненные расчеты указывают на то, что 95 %-ные доверительные интервалы для рассчитанных «искаженных» величин Sb для умеренных и сильных помех относительно невелики и совпадают с доверительными интервалами «истинных» значений Sb. Интересно, что даже для очень больших помех эти интервалы значительно перекрываются. Следовательно, при ориентации палеомагнитных образцов при изучении амплитуд древних геомагнитных вариаций нет необходимости отказываться от использования магнитного компаса в пользу альтернативных средств ориентации.
Следует отметить при этом, что на точность результата, независимо от способа ориентации палеомагнитных образцов, существенно влияет число исследуемых потоков. Так, уменьшение числа потоков от 60 до 20 может привести к почти двукратному увеличению ширины доверительного интервала (сравните фрагменты рис. 6, в, ж, л, и рис. 6, г, з, м).
Выполненное моделирование показывает, что отклонение искаженного полюса от «истинного» крайне невелико при умеренном и большом уровне помех. При этом оно меньше точности определения палеомагнитного полюса, обычно достигаемой при палеомагнитных исследованиях.
При введении очень сильных помех отклонение «искаженного» полюса от истинного возрастает и может достигать значений 5–6°, существенных при интерпретации палеомагнитных данных. Однако в этом случае также сильно увеличивается внутрисайтовый разброс, значения α95 становятся больше 15° и простая селекция данных по этому параметру позволяет избежать ошибок определения положения палеомагнитного полюса, связанных с наличием больших погрешностей при определении ориентации палеомагнитных образцов.
В завершение рассмотрим вопрос о влиянии систематических ошибок при использовании магнитного компаса при отборе палеомагнитных образцов. Такие систематические ошибки в масштабах сайтов (потоков) могут возникать за счет, например, локальных отклонений геомагнитного поля от референтной модели IGRF, используемой для расчета магнитного склонения, или за счет однонаправленного воздействия магнитного поля, связанного с намагниченностью исследуемого потока, на замеры магнитного компаса. Последнее представляется довольно вероятным в случае отбора образцов сайта в непосредственной близости друг от друга, как это случается в практике палеомагнитных исследований.
Для учета такого влияния в шаг 3 модели вносится дополнительный элемент: помимо случайной помехи в исходный сигнал теперь будет вноситься также систематическая погрешность, одинаковая для всех образцов каждого сайта, но, естественно, отличающаяся для разных сайтов. Значения этой погрешности авторы берут случайным образом из нормального распределения с нулевым средним, аппроксимирующего наблюденное распределение отклонений средних по сайтам склонений, измеренных с помощью магнитного метода, от средних по сайтам склонений, измеренных альтернативными методами (см. рис. 1, б). Это нормальное распределение имеет стандартное отклонение σsyst=11°. Для того чтобы усилить универсальность выводов, авторы рассматривают также случаи σsyst=5° и σsyst=22°.
Результаты выполненных таким образом вычислений (для случая умеренных случайных помех σ=8°, k=25 и N=60) представлены на рис. 10. При сравнении с аналогичным примером (см. рис. 6, а), не учитывающим систематическую погрешность, видно, что внесение последней приводит к небольшому (около 1° на экваторе) увеличению угловой разницы между «истинными» и «искаженными» значениями Sb и сколько-нибудь заметно не отражается на ширине доверительных интервалов. При движении к широте 60° эти угловые различия уменьшаются практически до нуля, а затем снова незначительно растут из-за эффекта, который обсуждался выше.

Рис. 10. Сравнение широтных зависимостей Sb для «искаженных»
и для «неискаженных» данных с учетом возможных систематических погрешностей (σsyst) (а).
Голубые кружки и соответствующие им вертикальные линии показывают значения Sb и их 95%-ные доверительные интервалы, рассчитанные по «неискаженным» данным. Оранжевые кружки и соответствующие вертикальные линии показывают значения Sb и их 95%-ные доверительные интервалы, рассчитанные по «искаженным» данным. Угловые смещения средних «искаженных» значений Sb относительно «истинных» в зависимости от широты (б). Расчеты сделаны для случая числа модельных вулканических потоков (сайтов) N=60, кучностей внутрисайтовых распределений k=100 случайных помех (шумов), σ=8° с учетом внутрисайтового разброса и величины cutoff=45°.
Fig. 10. Comparison of latitude dependencies Sb for “distorted”
and for “undistorted” data, considering possible systematic distortions (σsyst) (а).
The blue circles and their corresponding vertical lines show the values of Sb and their 95 % confidence intervals calculated from "undistorted" data. The orange circles and corresponding vertical lines show the values of Sb and their 95 % confidence intervals calculated from "distorted" data. Angular offsets of the average "distorted" Sb values relative to the "undistorted" ones, depending on latitude (б). Calculations are made for the case of the number of model volcanic flows (sites) N=60, the precision parameter k=100 distortions σ=8°, considering the intra-site spread and the cutoff=45°.
При увеличении систематической погрешности (σsyst=11° и σsyst=22°) угловые различия между «истинными» и «искаженными» Sb увеличиваются, при этом ширина доверительных интервалов для «искаженных» значений Sb медленно растет. Интересно отметить, что обсуждавшийся выше эффект увеличения кучности «искаженных» направлений начиная с σsyst=11° практически перестает чувствоваться.
Наиболее важным результатом, однако, является то, что уже с шестидесятых широт и выше значения Sb, полученные по «искаженным» данным, слабо отличаются от таковых, полученных по «истинным» данным. Для умеренных систематических ошибок σsyst=11°, отражающих, по-видимому, реальную ситуацию, эта величина становится меньше 1°.
Как можно видеть из рис. 11, введение систематической ошибки не приводит к существенному искажению положения палеомагнитного полюса. Даже при очень сильной систематической ошибке σsyst=22° смещение «искаженного» полюса относительно «истинного» не превышает 3°, что вполне соизмеримо с обычной погрешностью определения палеомагнитного полюса.
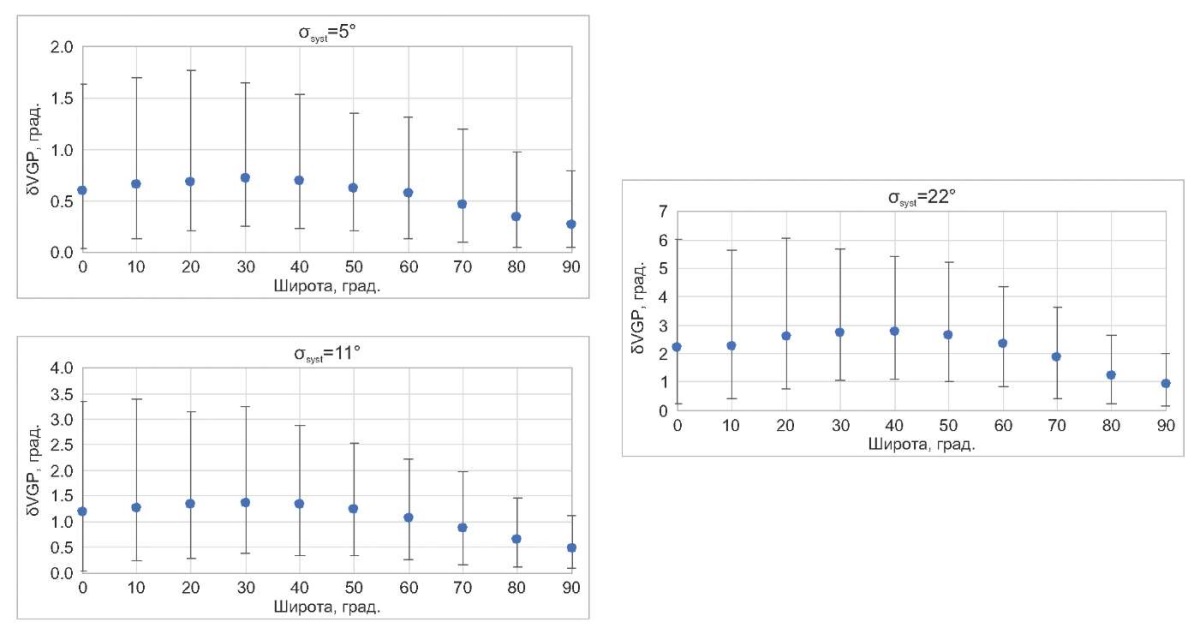
Рис. 11. Ошибка определения положения палеомагнитного полюса (δVGP)
с учетом возможных систематических погрешностей (σsyst).
Расчет сделан для случая числа сайтов N=60, кучности k=25 и случайных помех (шумов) σsyst=8°. Угловые отличия (и соответствующие доверительные интервалы) палеомагнитных полюсов рассчитаны путем сравнения «искаженных» и «неискаженных» данных.
Fig. 11. Discrepancies in determining the position of the paleomagnetic pole (δVGP),
considering possible systematic distortions (σsyst).
The calculation is made for the case of the number of sites N=60, the precision parameter k=25 and distortions σsyst=8°. Angular differences (and corresponding confidence intervals) of paleomagnetic poles calculated from "distorted" and "undistorted" data.
5. ЗАКЛЮЧЕНИЕ
Расчетные величины амплитуд палеовековых вариаций и расчетные положения палеомагнитных полюсов при достаточно большом (несколько десятков) числе сайтов слабочувствительны к умеренным и даже относительно большим ошибкам ориентации палеомагнитных образцов, связанных с применением магнитного компаса.
Очень большие ошибки ориентации образцов приводят к значительному увеличению внутрисайтового разброса, что позволяет обнаруживать и отбраковывать соответствующие сайты по большой (например, >15°) величине α95.
Влияние искажений, связанных с использованием магнитного компаса, на точность определения положения палеомагнитного полюса и амплитуды древних геомагнитных вариаций зависит от широты. На приэкваториальных широтах это влияние максимально, на средних – минимально.
При наличии систематической ошибки ориентации палеомагнитных образцов внутри сайта наибольшие отклонения значений Sb и палеомагнитных полюсов от истинных наблюдаются в интервале широт до 60°, при бóльших широтах эти отклонения становятся незначительными.
6. ЗАЯВЛЕННЫЙ ВКЛАД АВТОРОВ / CONTRIBUTION OF THE AUTHORS
Все авторы внесли эквивалентный вклад в подготовку рукописи, прочли и одобрили финальную версию перед публикацией.
All authors made an equivalent contribution to this article, read and approved the final manuscript.
7. РАСКРЫТИЕ ИНФОРМАЦИИ / DISCLOSURE
Авторы заявляют об отсутствии конфликта интересов, связанного с этой рукописью.
The authors declare that they have no conflicts of interest relevant to this manuscript.
1. Под «сильномагнитными» здесь будем понимать породы с намагниченностью порядка таковой, характерной для основных пород, в частности базальтов. Типичные величины намагниченности последних составляют от нескольких единиц до первых десятков A/м, что на два-три порядка выше намагниченности красноцветных осадочных пород (единицы – десятки мA/м), широко используемых для палеомагнитных исследований.
2. При использовании магнитного компаса существует практика отбраковки сильномагнитных пород, существенно влияющих на показания магнитного компаса. Эта практика состоит в отслеживании поведения стрелки магнитного компаса при приближении последнего к обнажению. Объект считается пригодным для отбора с помощью магнитного компаса, если при таком приближении стрелка компаса существенно не смещается.
3. Под палеомагнитным полюсом здесь понимается средний полюс, рассчитанный по совокупности VGP, полученных по всем изученным вулканическим потокам.
Список литературы
1. Alken P., Thébault E., Beggan C.D., Amit H., Aubert J., Baerenzung J., Bondar T.N., Brown W.J. et al., 2021. International Geomagnetic Reference Field: The Thirteenth Generation. Earth, Planets and Space 73, 49. https://doi.org/10.1186/s40623-020-01288-x.
2. Biggin A.J., van Hinsbergen D.J.J., Langereis C.G., Straathof G.B., Deenen M.H.L., 2008. Geomagnetic Secular Variation in the Cretaceous Normal Superchron and in the Jurassic. Physics of the Earth and Planetary Interiors 169 (1–4), 3–19. https://doi.org/10.1016/j.pepi.2008.07.004.
3. Butler R.F., 1992. Paleomagnetism: Magnetic Domains to Geological Terranes. Blackwell Science Inc., New York, 336 p.
4. Cox A., 1970. Latitude Dependence of the Angular Dispersion of the Geomagnetic Field. Geophysical Journal International 20 (3), 253–269. https://doi.org/10.1111/j.1365-246X.1970.tb06069.x.
5. Cromwell G., Tauxe L., Staudigel H., Constable C.G., Koppers A.A.P., Pedersen R.-B., 2013. In Search of Long-Term Hemispheric Asymmetry in the Geomagnetic Field: Results from High Northern Latitudes. Geochemistry, Geophysics, Geosystems 14 (8), 3234–3249. https://doi.org/10.1002/ggge.20174.
6. Deenen M.H.L., Langereis C.G., van Hinsbergen D.J.J., Biggin A.J., 2011. Geomagnetic Secular Variation and the Statistics of Palaeomagnetic Directions. Geophysical Journal International 186 (2), 509–520. https://doi.org/10.1111/j.1365-246X.2011.05050.x.
7. Døssing A., Riishuus M.S., Niocaill C.M., Muxworthy A.R., Maclennan J., 2020. Late Miocene to Late Pleistocene Geomagnetic Secular Variation at High Northern Latitudes. Geophysical Journal International 222 (1), 86–102. https://doi.org/10.1093/gji/ggaa148.
8. Doubrovine P.V., Veikkolainen T., Pesonen L.J., Piispa E., Ots S., Smirnov A.V., Kulakov E.V., Biggin A.J., 2019. Latitude Dependence of Geomagnetic Paleosecular Variation and Its Relation to the Frequency of Magnetic Reversals: Observations from the Cretaceous and Jurassic. Geochemistry, Geophysics, Geosystems 20 (3), 1240–1279. https://doi.org/10.1029/2018GC007863.
9. Fukuma K., Muramatsu T., 2022. Orienting Paleomagnetic Drill Cores Using a Portable GPS Compass. Earth Planets Space 74, 136. https://doi.org/10.1186/s40623-022-01699-y.
10. Khramov A.N. (Ed.), 1982. Paleomagnetology. Nedra, Leningrad, 312 p. (in Russian) [Палеомагнитология / Ред. А.Н. Храмов. Л.: Недра, 1982. 312 с.].
11. Lebedev I.E., Bobrovnikova E.M., Tikhomirov P.L., Eid B., Lhuillier F., Pavlov V.E., 2022. Amplitude of Secular Geomagnetic Variation in Late Cretaceous Based on Paleomagnetic Studies of the Okhotsk–Chukotka Volcanic Belt from Upper Reaches of Malyi Anyui River, West Chukotka. Izvestiya, Physics of the Solid Earth 58, 185–202. https://doi.org/10.1134/S1069351322020045.
12. Lebedev I.E., Pavlov V.E., Minaev P.A., 2023. Orientation Errors of Paleomagnetic Samples When Using a Magnetic Compass and Possible Ways to Overcome Them. Uchenye Zapiski Kazanskogo Universiteta. Seriya Estestvennye Nauki 165 (4), 633–645 (in Russian) [Лебедев И.Е., Павлов В.Э., Минаев П.А. Ошибки ориентирования палеомагнитных образцов при использовании магнитного компаса и возможные пути их преодоления // Ученые записки Казанского университета. Серия Естественные науки. Т. 165. № 4. С. 633–645]. https://doi.org/10.26907/2542-064X.2023.4.633-645.
13. Lhuillier F., Lebedev I.E., Tikhomirov P.L., Pavlov V.E., 2023. High-Latitude Geomagnetic Secular Variation at the End of the Cretaceous Normal Superchron Recorded by Volcanic Flows from the Okhotsk-Chukotka Volcanic Belt. Journal of Geophysical Research: Solid Earth 129 (1), e2023JB027550. https://doi.org/10.1029/2023JB027550.
14. McElhinny M.W., McFadden P.L., 1997. Palaeosecular Variation over the Past 5 Myr Based on a New Generalized Database. Geophysical Journal International 131 (2), 240–252. https://doi.org/10.1111/j.1365-246X.1997.tb01219.x.
15. Tauxe L., Kent D.V., 2004. A Simplified Statistical Model for the Geomagnetic Field and the Detection of Shallow Bias in Paleomagnetic Inclinations: Was the Ancient Magnetic Field Dipolar? In: J.E.T. Channell, D.V. Kent, W. Lowrie, J.G. Meert (Eds), Timescales of the Paleomagnetic Field. Geophysical Monograph Series. Vol. 145. AGU, Washington, p. 101–115. https://doi.org/10.1029/145GM08.
16. Tauxe L., Shaar R., Jonestrask L., Swanson-Hysell N.L., Minnett R., Koppers A.A.P., Constable C.G., Jarboe N., Gaastra K., Fairchild L., 2016. PmagPy: Software Package for Paleomagnetic Data Analysis and a Bridge to the Magnetics Information Consortium (MagIC) Database. Geochemistry, Geophysics, Geosystems 17 (6), 2450–2463. https://doi.org/10.1002/2016GC006307.
17. Vandamme D., 1994. A New Method to Determine Paleosecular Variation. Physics of the Earth and Planetary Interiors 85 (1–2), 131–142. https://doi.org/10.1016/0031-9201(94)90012-4.
Об авторах
Д. А. УшаковРоссия
123242, Москва, ул. Большая Грузинская, 10, стр. 1
И. Е. Лебедев
Россия
123242, Москва, ул. Большая Грузинская, 10, стр. 1
В. Э. Павлов
Россия
123242, Москва, ул. Большая Грузинская, 10, стр. 1
Рецензия
Для цитирования:
Ушаков Д.А., Лебедев И.Е., Павлов В.Э. ВЛИЯНИЕ ОШИБОК ОРИЕНТАЦИИ, СВЯЗАННЫХ С ИСПОЛЬЗОВАНИЕМ МАГНИТНОГО КОМПАСА, НА ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ПАЛЕОМАГНИТНОГО ПОЛЮСА И АМПЛИТУДЫ ДРЕВНИХ ГЕОМАГНИТНЫХ ВАРИАЦИЙ. Геодинамика и тектонофизика. 2024;15(2):0752. https://doi.org/10.5800/GT-2024-15-2-0752. EDN: ADJXPH
For citation:
Ushakov D.A., Lebedev I.E., Pavlov V.E. INFLUENCE OF ORIENTATION ERRORS ASSOCIATED WITH THE USE OF A MAGNETIC COMPASS ON THE ACCURACY OF DETERMINING THE POSITION OF THE PALEOMAGNETIC POLE AND THE AMPLITUDE OF PALEOSECULAR VARIATIONS. Geodynamics & Tectonophysics. 2024;15(2):0752. (In Russ.) https://doi.org/10.5800/GT-2024-15-2-0752. EDN: ADJXPH



















































