Перейти к:
МЕТОДИКА ОБЪЕДИНЕНИЯ КОСЕЙСМИЧЕСКИХ СМЕЩЕНИЙ ЗЕМНОЙ КОРЫ ПО ДАННЫМ РАЗНОРОДНЫХ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ: НА ПРИМЕРЕ МЕГАЗЕМЛЕТРЯСЕНИЯ ТОХОКУ 11.03.2011 г., Mw 9.1
https://doi.org/10.5800/GT-2024-15-1-0736
EDN: HQCNAT
Аннотация
Сильнейшие землетрясения с магнитудой Mw 8–9 порождают косейсмические смещения земной коры, охватывающие целые регионы мира и регистрируемые по наблюдениям в независимых геодезических ГНСС-сетях. Данные этих сетей обрабатываются с применением разных алгоритмов и методик анализа спутниковых наблюдений, способов расчета косейсмического смещения, реализаций системы координат. Эти факторы приводят к «несогласованности» объединяемых полей смещений и появлению дополнительных ошибок в результатах моделирования косейсмических эффектов. В работе предлагается методика объединения полей косейсмических смещений земной коры, полученных в дальней относительно очага зоне по данным разнородных ГНСС-сетей. Результаты применения предлагаемой методики продемонстрированы на примере объединения полей косейсмических смещений территории Китая, Южной Кореи и юга Дальнего Востока Российской Федерации, инициированных катастрофическим землетрясением Тохоку 11 марта 2011 г., Mw 9.1, а также расчета и анализа единого поля косейсмических деформаций исследуемого региона.
Ключевые слова
Для цитирования:
Шестаков Н.В., Герасименко М.Д., Кишкина А.К., Быков В.Г., Пупатенко В.В., Прытков А.С., Василенко Н.Ф., Жижерин В.С., Яковенко С.В. МЕТОДИКА ОБЪЕДИНЕНИЯ КОСЕЙСМИЧЕСКИХ СМЕЩЕНИЙ ЗЕМНОЙ КОРЫ ПО ДАННЫМ РАЗНОРОДНЫХ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ: НА ПРИМЕРЕ МЕГАЗЕМЛЕТРЯСЕНИЯ ТОХОКУ 11.03.2011 г., Mw 9.1. Геодинамика и тектонофизика. 2024;15(1):0736. https://doi.org/10.5800/GT-2024-15-1-0736. EDN: HQCNAT
For citation:
Shestakov N.V., Gerasimenko М.D., Kishkina А.К., Bykov V.G., Pupatenko V.V., Prytkov А.S., Vasilenko N.F., Zhizherin V.S., Yakovenko S.V. METHODOLOGY OF COSEISMIC DISPLACEMENTS COMBINATION OBTAINED BY DATA STEMMING FROM HETEROGENEOUS GEODETIC NETWORKS: ON THE EXAMPLE OF THE GREAT 2011 TOHOKU EARTHQUAKE, Mw 9.1. Geodynamics & Tectonophysics. 2024;15(1):0736. (In Russ.) https://doi.org/10.5800/GT-2024-15-1-0736. EDN: HQCNAT
1. ВВЕДЕНИЕ
Многочисленные исследования, посвященные изучению сильнейших землетрясений начала XXI в. – Суматра-Андаманского (26.12.2004 г., Mw 9.1), Чилийского (27.02.2010 г., Mw 8.8), Тохоку (11.03.2011 г., Mw 9.1) и Охотоморского глубокофокусного землетрясения (24.05.2013 г., Mw 8.3), показали, что инициированные такими сейсмическими событиями непосредственно после главного толчка смещения и деформации земной коры, называемые косейсмическими, могут охватывать огромные территории, площадью в миллионы квадратных километров [Tregoning et al., 2013; Shestakov et al., 2014]. Основным способом регистрации и изучения таких движений являются методы ГНСС-позиционирования, которые позволяют определять их величины с точностью от субдециметра до нескольких сантиметров в режиме реального времени [Fratarcangeli et al., 2018] и с ошибками порядка нескольких миллиметров при ретроспективном анализе. Информация о косейсмических смещениях чрезвычайно важна для моделирования физики и динамики развития различных процессов в очагах мощных землетрясений, определения величин и направлений смещений морского дна в случае подводного сейсмического события и принятия решения о его цунамигенности, моделирования волн цунами, а также разработки и функционирования систем раннего предупреждения о них [Blewitt et al., 2009], расчета и анализа деформаций земной коры, а также параметров других косейсмических эффектов и процессов. В силу больших размеров области, охватываемой косейсмическими подвижками при сильнейших землетрясениях, они не могут быть зарегистрированы с достаточной полнотой и пространственным разрешением с использованием только одной геодезической ГНСС-сети глобального, например сеть IGS (https://network.igs.org/), или регионального (национального) масштаба, например таких, как сеть GEONET, Япония [Takamatsu et al., 2023], сеть CMONOC, Китай [Wang, Shen, 2020], Камчатская ГНСС-сеть [Levin et al., 2014] и Байкало-Монгольская ГНСС-сеть [Lukhnev et al., 2010] РФ и другие подобные геодинамические сети. В связи с этим для решения перечисленных выше задач необходима совместная математическая обработка данных двух и более независимых геодезических сетей, что возможно далеко не всегда, так как в обширных ГНСС-сетях такая обработка сложна и требует больших затрат вычислительных и временных ресурсов. Кроме того, получение исходных данных спутниковых измерений обычно сопряжено с труднопреодолимыми бюрократическими формальностями, в то время как результаты обработки – оценки косейсмических смещений – публикуются открыто в научной печати. Таким образом, наиболее простой и обеспечивающий достаточную точность получаемых результатов путь – объединение независимо полученных полей (групп) косейсмических смещений, которое не может быть выполнено простым сведением подвижек в одну таблицу, как поступают многие авторы, поскольку математическая обработка ГНСС-данных в независимых геодезических сетях выполняется с применением различающихся алгоритмов и методик анализа спутниковых данных, способов расчета косейсмических смещений, разных реализаций системы координат и т.д. Это приводит к появлению дополнительных ошибок в результатах моделирования геофизических процессов и явлений из-за «несогласованности» объединяемых полей смещений. Например, приводимые в публикациях [Banerjee et al., 2005; Hashimoto et al., 2006] оценки косейсмических подвижек, инициированных катастрофическим Суматро-Андаманским землетрясением на более чем десяти пунктах ГНСС-сети IGS, демонстрируют существенное (до 7 мм по абсолютной величине) различие величин их плановых компонент. С учетом того, что величины смещений в дальней относительно очага землетрясения зоне, регистрируемые на расстояниях от нее от нескольких сотен до тысячи километров и более, редко превосходят 10–20 мм, такие различия в оценках смещений могут заметно повлиять на результаты моделирования параметров очага землетрясения, оценку его магнитуды и другие интересующие специалистов параметры.
В данной работе предлагается методика объединения (комбинирования) независимо полученных полей косейсмических смещений земной коры в дальней относительно очага сильного землетрясения зоне, минимизирующая различия между ними. Эффективность методики иллюстрируется на примере получения объединенного поля косейсмических подвижек и деформаций юго-восточной части Евразийского континента, инициированных землетрясением Тохоку 11.03.2011 г.
2. МЕТОДИКА КОМБИНИРОВАНИЯ КОСЕЙСМИЧЕСКИХ СМЕЩЕНИЙ
Преобразование Гельмерта наиболее часто используется для трансформирования координат и скоростей смещений геодезических пунктов из одной пространственной прямоугольной системы координат в другую. В данной работе предлагается методика применения этого преобразования для корректного объединения косейсмических смещений, поскольку они также являются разностями координат, полученными до и после землетрясения. Каждое смещение можно рассматривать как отдельное квазиизмерение. В идеале косейсмические смещения, вычисленные на одном и том же пункте, но разными способами, должны быть одинаковы, если для их получения используется один и тот же набор ГНСС-измерений и других исходных данных. На практике это не так вследствие причин, описанных во введении. Поскольку данные факторы, по крайней мере отчасти, закономерно воздействуют на все измерения в группе, результат такого влияния можно интерпретировать как различия между системами координат, в которых определены смещения в комбинируемых группах. Таким образом, проблема корректного комбинирования смещений сводится к задаче трансформирования их в единую систему координат, которая может быть зафиксирована совокупностью косейсмических смещений одной из объединяемых групп, имеющих наиболее надежно и точно определенные значения подвижек. Иными словами, одна из комбинируемых групп квазиизмерений выбирается «опорной», а все остальные измерения «наилучшим образом вписываются» в нее.
Кратко рассмотрим основные особенности применения преобразования Гельмерта в приложении к косейсмическим перемещениям земной поверхности. Пусть необходимо объединить две группы косейсмических смещений. Для общности рассуждений рассмотрим 3-мерный случай. Обозначим в прямоугольной пространственной геоцентрической системе координат (ГСК) вектор косейсмических подвижек i-го пункта сети, входящего в одну из групп объединяемых квазиизмерений, как
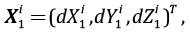
а результат его преобразования в другую группу:
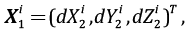
где dX, dY, dZ – величины смещений пункта по соответствующим осям ГСК, а нижний индекс обозначает принадлежность к соответствующей группе комбинируемых смещений. При трансформировании смещений на произвольном количестве пунктов n размерность векторов перемещений X1 и X2 равна 3n×1. Для определения элементов вектора параметров трансформирования θ удобно воспользоваться выражением [Altamimi et al., 2002]:
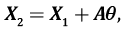 (1)
(1)
где
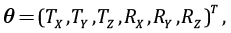 (2)
(2)
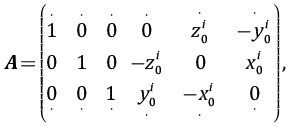 (3)
(3)
В выражении (3) приведен блок, соответствующий i-му опорному пункту, а 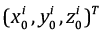 – вектор его приближенных координат в ГСК. Следует особо отметить, что масштабный коэффициент не вычисляется, поскольку ГНСС-системы обеспечивают единство масштаба в разных спутниковых сетях с достаточной для практических целей точностью.
– вектор его приближенных координат в ГСК. Следует особо отметить, что масштабный коэффициент не вычисляется, поскольку ГНСС-системы обеспечивают единство масштаба в разных спутниковых сетях с достаточной для практических целей точностью.
Если определены смещения на некотором количестве «опорных» пунктов k≥3, входящих в обе объединяемые группы, решение системы уравнений (1) методом наименьших квадратов дает оценку:
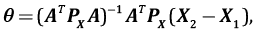 (4)
(4)
где PX – весовая матрица разностей смещений на общих пунктах, входящих обе группы. От ее выбора существенно зависит результат трансформирования. В простейшем случае PX=I – единичная матрица, т.е. все квазиизмерения считаются равноточными, что, как правило, справедливо только в первом приближении. Для более корректного построения PX используются ковариационные матрицы комбинируемых косейсмических смещений KX₁ и KX₂, которые получают по результатам математической обработки ГНСС-измерений.
На практике смещения пунктов, как правило, определяют не в ГСК, а в некоторой локальной системе координат (ЛСК), начало которой отнесено к поверхности Земли, т.е. векторами вида
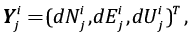
где 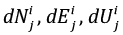 – величины перемещений по соответствующим осям ЛСК для i-го пункта геодезической сети, относящиеся к соответствующей комбинируемой группе j(j=1,2). Начало ЛСК обычно относят к какому-либо положению пункта перед его косейсмическим смещением (рис. 1), задаваемым пространственными прямоугольными и геодезическими координатами – широтой и долготой B0, L0.
– величины перемещений по соответствующим осям ЛСК для i-го пункта геодезической сети, относящиеся к соответствующей комбинируемой группе j(j=1,2). Начало ЛСК обычно относят к какому-либо положению пункта перед его косейсмическим смещением (рис. 1), задаваемым пространственными прямоугольными и геодезическими координатами – широтой и долготой B0, L0.
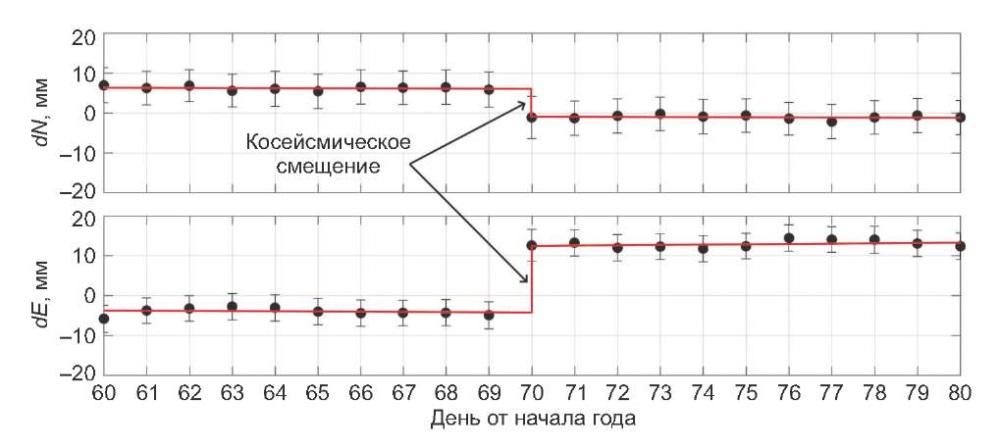
Рис. 1. Пример оценивания величин косейсмических смещений
по направлениям «Север – Юг» (dN) и «Восток – Запад» (dE) в локальной системе координат,
инициированных землетрясением Тохоку 11.03.2011 г. (70-й день от начала года),
на основе рядов среднесуточных пространственных положений ГНСС-станции «CHAN» (КНР).
Планками показаны величины среднеквадратических ошибок определения координат.
Красной линией дана аппроксимационная кривая,
построенная по методу наименьших квадратов.
Fig. 1. The example of estimating of the values of coseismic displacements
in the directions "North-South" (dN) and "East-West" (dE) in the local coordinate system,
initiated by the Great 2011 Tohoku earthquake (70th day of the year),
based on the series of average daily spatial positions of CHAN GNSS-station (China).
The bars show the values of the root mean square errors of the coordinates.
The red line denotes the approximation curve constructed by using the least squares method.
Для преобразования смещений из ЛСК в ГСК используются известные выражения (см., например [Hofmann-Wellenhof et al., 2008]).
Результаты преобразования существенно зависят от структуры ковариационной матрицы вектора смещений. Если используются только среднеквадратические ошибки компонент смещений пунктов, то матрица 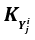 будет диагональной. Если вычислены ковариации между компонентами смещения станции, то
будет диагональной. Если вычислены ковариации между компонентами смещения станции, то 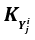 будет полной. Преобразование общей ковариационной матрицы
будет полной. Преобразование общей ковариационной матрицы 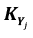 из ЛСК в ГСК, состоящей из k общих пунктов, принадлежащих к группе j, производится в соответствии с известным законом распространения ковариаций.
из ЛСК в ГСК, состоящей из k общих пунктов, принадлежащих к группе j, производится в соответствии с известным законом распространения ковариаций.
Поскольку в выражении (4) используется разность двух групп смещений X2–X1, соответствующая ковариационная матрица будет равна 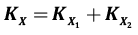 , а весовая матрица получается из выражения
, а весовая матрица получается из выражения 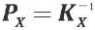 .
.
Вышеописанная методика позволяет реализовать достаточно простой алгоритм определения параметров и выполнения трансформирования косейсмических смещений с использованием подвижек на k общих пунктах:
- преобразование на общих пунктах смещений и их ковариационных матриц из ЛСК в ГСК;
- формирование весовой матрицы PX;
- построение «конфигурационной» матрицы Aпо формуле (3);
- вычисление при помощи выражения (4) элементов вектора θ;
- трансформирование смещений одной группы в другую с использованием вычисленных на шаге 4 параметров по формуле (1). Предварительно для трансформируемых смещений, не входящих в группу kобщих пунктов, необходимо выполнить шаги 1–3. Матрица A в этом случае строится уже для всех n трансформируемых пунктов;
- преобразование полученных смещений и их ковариационных матриц обратно из ГСК в ЛСК. Реализующий данный алгоритм программный код, написанный для программной среды MATLAB, может быть получен по запросу у авторов.
Качество выполненного преобразования оценивается на основе анализа величин разностей значений трансформированных и исходных косейсмических смещений, вычисленных на общих пунктах (невязки). Чем больше опорных пунктов использовано, тем надежнее результат трансформации. Значения невязок, как уже отмечалось, в «идеальном случае» должны быть равны нулю, но на практике достаточно, если они не будут превосходить первые миллиметры. Невязки на некоторых опорных пунктах могут значительно превышать эту величину, что может являться следствием грубых ошибок определения смещений на данной станции в одной из комбинируемых групп, а также действия ряда других факторов. Такие пункты удаляются из состава опорных, и процедура трансформирования повторяется до тех пор, пока невязки всех общих станций не достигнут приемлемого уровня.
3. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МЕТОДИКИ
Рассмотрим применение вышеописанной методики на примере объединения полей косейсмических смещений земной коры, инициированных на территории Китая, Республики Корея и в южной части Дальнего Востока России мегаземлетрясением Тохоку 11.03.2011 г., Mw 9.1, т.е. в дальней относительно очага зоне.
Изучению и моделированию горизонтальных косейсмических подвижек на территории Японских островов по данным японской геодинамической ГНСС-сети GEONET посвящена обширная литература (см., например, статьи в сборниках [Pollitz et al., 2011; Iinuma et al., 2011]). Смещения от 2 до 50 мм охватили всю восточную часть Евразийского континента, включая территории Корейского полуострова, Китая, Западной Монголии, юго-востока России [Shestakov et al., 2012]. Данный регион находится под влиянием эффектов взаимодействия Евразийской, Северо-Американской, Тихоокеанской, а также удаленной Индийской литосферной плиты. Рядом исследователей предполагается, что значительная часть региона входит в состав Амурской микроплиты [Zonenshain, Savostin, 1981; Heki et al., 1999; Ashurkov et al., 2016]. Исследованию современной геодинамической активности региона и кинематики Амурской микроплиты по данным ГНСС-наблюдений посвящены многие работы отечественных и зарубежных авторов (см., например [Lukhnev et al., 2010; Ashurkov et al., 2016; Wang, Shen, 2020]).
Однако получению пространственного распределения косейсмических движений земной коры на востоке Евразийского континента, расположенного на значительном удалении от очага землетрясения Тохоку, посвящено очень ограниченное число публикаций [Wang et al., 2011; Baek et al., 2012; Shestakov et al., 2012]. В каждой из них анализируются данные программно-математической обработки отдельной ГНСС-сети, полученные с использованием разных программных средств, таких как Gamit/Globk (http://geoweb.mit.edu/gg/) и Bernese GNSS Software (http://www.bernese.unibe.ch/), несовпадающих наборов исходных пунктов, фиксирующих систему координат, методик обработки спутниковых измерений и расчета косейсмических смещений на пунктах анализируемой геодезической сети. Схема расположения пунктов этих сетей представлена на рис. 2. Авторами по данным комплексной геодинамической ГНСС-сети ДВО РАН [Bykov et al., 2020], ГНСС-станции ТОИ ДВО РАН и нескольких базовых станций, принадлежащих коммерческим организациям, определены плановые косейсмические смещения юга Дальнего Востока России. В этом же решении были получены косейсмические подвижки ряда пунктов сети IGS (рис. 2). В табл. 1 приведены оценки расширенного и уточненного, по сравнению с данными из работы [Shestakov et al., 2012], набора смещений, вычисленные на пунктах, не входящих в сеть IGS. Наблюдения в геодинамической ГНСС-сети CMONOC были использованы авторами работы [Wang et al., 2011] для получения векторов косейсмических подвижек почти 80 пунктов, расположенных на территории Китая. Параметры косейсмических смещений Корейского полуострова вычислены по данным наблюдений на более чем 70 пунктах южно-корейской ГНСС-сети и приводятся в работе [Baek et al., 2012]. Часть смещений в каждой из вышеуказанных групп также определена на одних и тех же пунктах глобальной сети IGS, расположенных в исследуемом регионе и за его пределами (рис. 2). Вертикальные перемещения в дальней зоне зарегистрированы не были, поэтому далее не рассматриваются.
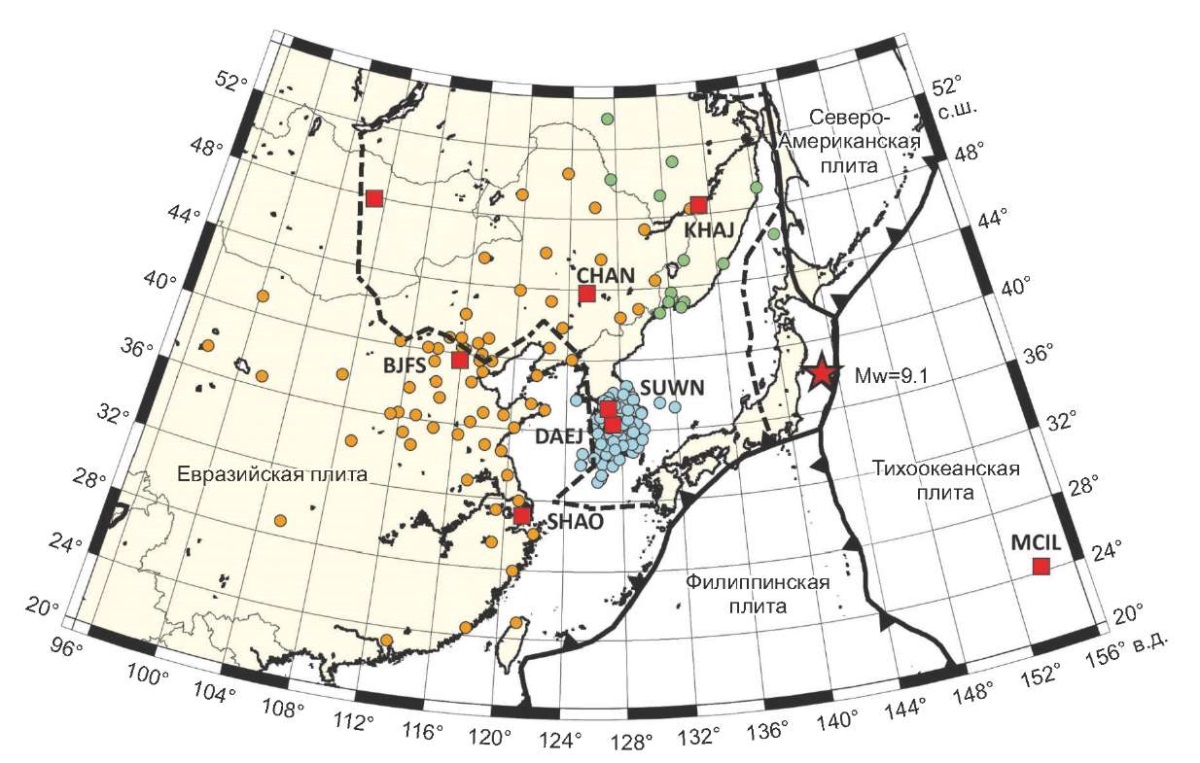
Рис. 2. Схема расположения пунктов анализируемых геодезических сетей.
Зеленые кружки − российские, оранжевые − китайские,
голубые − южно-корейские ГНСС-станции.
Красными квадратиками показаны пункты, смещения на которых вычислены
по данным двух и более спутниковых сетей (опорные пункты).
Звездочкой отмечен эпицентр землетрясения Тохоку 2011 г.
Черные треугольники показывают направление субдукции.
Пунктирной линией обозначен один из вариантов положения границы
предполагаемой Амурской микроплиты [Bird, 2003].
Fig. 2. The scheme of the analyzed geodetic networks.
Green circles − Russian, orange − Chinese, blue − South Korea GNSS-stations.
The red squares show the sites joined to the couple or more GNSS-networks (reference points).
The asterisk marks the epicenter of the 2011 Tohoku earthquake.
Black triangles indicate the direction of subduction.
The dotted line denotes the boundary location
of the hypothesized Amurian microplate according to [Bird, 2003].
Таблица 1. Косейсмические смещения ГНСС-станций,
расположенных в южной части Дальнего Востока России
до и после трансформирования и их среднеквадратические ошибки
Table 1. Coseismic displacements of GNSS-stations
located in the southern part of the Russian Far East
before and after the transformation and their square errors
№ | Наименование пункта | Положение пункта | Косейсмические смещения по плановым компонентам ЛСК | ||||
Исходные | Трансформированные | ||||||
Широта | Долгота | dN, мм | dE, мм | dN, мм | dE, мм | ||
1 | ARTM | 43.360° | 132.196° | –20.6±2.4 | 35.6±2.6 | –20.6±2.6 | 39.3±2.8 |
2 | CHMN | 51.137° | 133.041° | –6.5±1.4 | 2.6±1.2 | –6.0±2.0 | 6.7±2.0 |
3 | GRNC | 43.698° | 132.166° | –19.0±1.4 | 32.4±2.0 | –19.0±1.7 | 36.1±2.3 |
4 | KULD | 49.236° | 131.738° | –7.9±1.4 | 6.3±1.6 | –7.4±1.9 | 10.2±2.1 |
5 | BLAG | 50.257° | 127.521° | –6.2±1.0 | 4.9±1.0 | –5.3±1.6 | 8.6±1.7 |
6 | VANB | 49.091° | 140.255° | –4.7±0.9 | 0.0±1.7 | –5.1±1.8 | 4.4±2.4 |
7 | ZEYA | 53.757° | 127.286° | –3.8±1.2 | 1.6±1.0 | –2.4±2.0 | 5.4±2.0 |
8 | SHUL | 42.581° | 131.157° | –15.9±2.2 | 37.1±2.5 | –15.9±2.4 | 40.8±2.7 |
9 | VLAD | 43.197° | 131.926° | –19.2±1.9 | 36.5±2.6 | –19.2±2.2 | 40.2±2.8 |
10 | LESZ | 45.469° | 133.385° | –18.8±3.4 | 21.7±2.7 | –18.8±3.6 | 25.6±3.0 |
11 | PART | 43.123° | 133.126° | –25.9±1.9 | 43.0±2.7 | –26.0±2.2 | 46.8±2.9 |
12 | NKHD | 42.828° | 132.891° | –26.0±2.1 | 43.8±3.1 | –26.1±2.3 | 47.5±3.3 |
13 | TERN | 45.062° | 136.601° | –33.4±6.8 | 20.9±7.5 | –33.6±6.9 | 24.9±7.6 |
14 | MONR | 46.246° | 141.259° | –12.5±2.9 | 7.7±3.6 | –13.1±3.3 | 11.9±3.9 |
По наблюдениям на общих (связующих) пунктах сети IGS и по методике, описанной в предыдущем разделе, поля косейсмических смещений на территории Дальнего Востока РФ и Южной Кореи были объединены с аналогичными данными по Китаю, выбранными в качестве «опорных», поскольку последние получены с использованием большого количества исходных пунктов (~100 глобально распределенных станций сети IGS) и расположены на гораздо более обширной территории. Комбинирование данных сети CMONOC и ГНСС-сетей, расположенных на российской территории, выполнено по набору смещений на восьми общих IGS-пунктах: BJFS, CHAN, DAEJ, KHAJ, MCIL, SHAO, SUWN, ULAB. Величины косейсмических подвижек на этих пунктах достаточно надежно определены. Вычисленные параметры трансформирования даны в табл. 2. Результаты трансформирования и смещений на опорных пунктах приведены в табл. 3, 4. Из анализа табл. 3 видно, что максимальная разница (по модулю) в величинах косейсмических смещений dS, полученных на этих пунктах авторами и китайскими специалистами, до трансформирования достигала 4.7 мм (среднее значение 3.3 мм), а после него уменьшилась до 1.2 мм (среднее значение 0.9 мм). Поле исходных и трансформированных косейсмических смещений на пунктах, расположенных на российской территории, показано на рис. 3, а.
Таблица 2. Вычисленные параметры трансформирования
в систему косейсмических смещений сети CMONOC (Китай, «SYSTEM 2»)
полей подвижек на пунктах российских и южно-корейских ГНСС-сетей («SYSTEM 1»)
Table 2. The calculated transformation parameters
from the coseismic displacements at the stations of Russian
and South Korean GNSS-networks ("SYSTEM 1")
into the system of coseismic slips at CMONOC network sites (China, "SYSTEM 2")
ГНСС-сеть | UWRMS, мм | TX, мм | TY, мм | TZ, мм | RX, угл. с∙10–3 | RY, угл. с∙10–3 | RZ, угл. с∙10–3 |
Российская | 0.25 | –19.0±5.4 | –3.3±4.9 | –15.8±5.0 | 0.28±0.17 | 0.58±0.16 | –0.33±0.16 |
Южно-корейская | 0.20 | –31.0±18.5 | 6.0±16.2 | –42.2±15.8 | 1.04±0.59 | 1.16±0.52 | –0.61±0.51 |
Таблица 3. Плановые косейсмические смещения в ЛСК
на общих пунктах для российских и китайских ГНСС-сетей
Table 3. Horizontal coseismic offsets determined in the local coordinate system
at the set of common sites of the Russian and Chinese GNSS-networks
Пункт | Трансформируемые (данная работа), «Система 1» | Опорные [Wang et al., 2011], «Система 2» | Трансформированные в «Систему 2» «Система 1*» | Разности (невязки) до трансформирования «Система 2» − «Система 1» | Разности (невязки) после трансформирования «Система 2» − «Система 1*» | |||||||
dN, мм | dE, мм | dN, мм | dE, мм | dN*, мм | dE*, мм | dN, мм | dE, мм | dS, мм | dN, мм | dE, мм | dS, мм | |
ULAB | 0.6±1.3 | 2.0±1.3 | 0.0±1.5 | 3.0±1.5 | 0.7±2.1 | 3.4±2.1 | 0.6 | 1.0 | 1.2 | –0.7 | –0.4 | 0.8 |
CHAN | –6.2±0.9 | 14.9±2.6 | –6.0±1.8 | 18.0±1.8 | –5.8±1.3 | 18.3±2.8 | 0.2 | 3.1 | 3.1 | –0.2 | –0.3 | 0.3 |
SHAO | 1.2±1.8 | 3.4±1.0 | 1.0±1.5 | 6.0±1.7 | 0.9±2.2 | 7.0±1.7 | –0.2 | 2.6 | 2.6 | 0.1 | –1.0 | 1.0 |
DAEJ | 2.0±1.4 | 18.4±2.4 | 2.0±1.8 | 23.0±1.9 | 1.9±1.7 | 21.9±2.6 | 0.0 | 4.6 | 4.6 | 0.1 | 1.1 | 1.1 |
MCIL | 6.4±1.8 | –8.0±2.3 | 6.0±2.1 | –6.0±2.3 | 5.6±3.2 | –6.1±3.9 | –0.4 | 2.0 | 2.0 | 0.4 | 0.0 | 0.4 |
BJFS | –1.4±1.3 | 2.9±1.0 | 0.0±2.1 | 6.0±2.1 | –1.2±1.6 | 5.7±1.4 | 1.4 | 3.1 | 3.4 | 1.2 | 0.3 | 1.3 |
KHAJ | –10.8±1.1 | 6.3±1.5 | –11.0±2.1 | 11.0±2.0 | –10.7±1.7 | 10.4±2.1 | –0.2 | 4.7 | 4.7 | –0.3 | 0.6 | 0.7 |
SUWN | 1.4±1.1 | 19.3±2.4 | 1.0±1.9 | 24.0±2.0 | 1.3±1.4 | 22.8±2.6 | –0.4 | 4.7 | 4.7 | –0.3 | 1.2 | 1.2 |
Минимальное значение (по модулю) | 0.0 | 1.0 | 1.2 | 0.1 | 0.0 | 0.3 | ||||||
Максимальное значение (по модулю) | 1.4 | 4.7 | 4.7 | 1.2 | 1.2 | 1.3 | ||||||
Среднее (по модулю) | 0.4 | 3.2 | 3.3 | 0.4 | 0.6 | 0.9 | ||||||
Примечание. «*» – трансформированные из «Системы 1» в «Систему 2» смещения.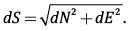 .
.
Note. "*" – the displacements transformed from "System 1" to "System 2". 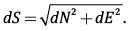 .
.
Таблица 4. Плановые косейсмические смещения в ЛСК
на общих пунктах для южно-корейских и китайских ГНСС-сетей
Table 4. Horizontal coseismic offsets determined in the local coordinate system
at the set of common sites of the South Korean and Chinese GNSS-networks
Пункт | Трансформируемые [Baek et al., 2012], «Система 1» | Опорные [Wang et al., 2011], «Система 2» | Трансформированные в «Систему 2» «Система 1*» | Разности (невязки) до трансформирования «Система 2» − «Система 1» | Разности (невязки) после трансформирования «Система 2» − «Система 1*» | |||||||
dN, мм | dE, мм | dN, мм | dE, мм | dN*, мм | dE*, мм | dN, мм | dE, мм | dS, мм | dN, мм | dE, мм | dS, мм | |
BJFS | –0.1±1.5 | 6.9±1.3 | 0.0±2.1 | 6.0±2.1 | 0.0±2.4 | 6.0±2.2 | 0.1 | –0.9 | 0.9 | 0.0 | 0.0 | 0.0 |
KHAJ | –11.2±1.3 | 7.6±1.2 | –11.0±2.1 | 11.0±2.0 | –10.7±2.7 | 10.8±2.5 | 0.2 | 3.4 | 3.4 | –0.4 | 0.2 | 0.4 |
CHAN | –7.0±1.4 | 18.1±1.3 | –6.0±1.8 | 18.0±1.8 | –6.3±1.9 | 19.0±1.8 | 1.0 | –0.1 | 1.0 | 0.3 | –0.9 | 1.0 |
SHAO | 1.7±1.4 | 6.2±1.1 | 1.0±1.5 | 6.0±1.7 | 0.8±2.3 | 6.2±2.1 | –0.7 | –0.2 | 0.7 | 0.2 | –0.2 | 0.3 |
DAEJ | 2.6±1.3 | 21.6±1.3 | 2.0±1.8 | 23.0±1.9 | 2.0±1.8 | 22.1±1.8 | –0.6 | 1.4 | 1.5 | –0.0 | 0.9 | 0.9 |
SUWN | 1.8±1.5 | 23.3±1.3 | 1.0±1.9 | 24.0±2.0 | 1.3±1.9 | 23.8±1.7 | –0.8 | 0.7 | 1.1 | –0.3 | 0.2 | 0.4 |
Минимальное значение (по модулю) | 0.1 | 0.1 | 0.7 | 0.0 | 0.0 | 0.0 | ||||||
Максимальное значение (по модулю) | 1.0 | 3.4 | 3.4 | 0.4 | 0.9 | 1.0 | ||||||
Среднее (по модулю) | 0.6 | 1.1 | 1.4 | 0.2 | 0.4 | 0.5 | ||||||
Примечание. «*» – трансформированные из «Системы 1» в «Систему 2» смещения.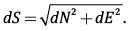 .
.
Note. "*" – the displacements transformed from “System 1” to “System 2”. 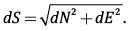 .
.
Аналогичная процедура проделана в отношении данных южно-корейской ГНСС-сети и CMONOC по набору из шести общих пунктов: BJFS, CHAN, DAEJ, KHAJ, SHAO, SUWN (см. рис. 2) Согласно табл. 4, максимальная разница (по модулю) величин косейсмических смещений dS, полученных на общих пунктах в решении из работы [Baek et al., 2012] и статьи [Wang et al., 2011] до трансформирования, достигает 3.4 мм (среднее значение 1.4 мм). После преобразования она уменьшилась до 1.0 мм (среднее значение 0.5 мм). Результаты трансформирования и исходные подвижки показаны на рис. 3, б.
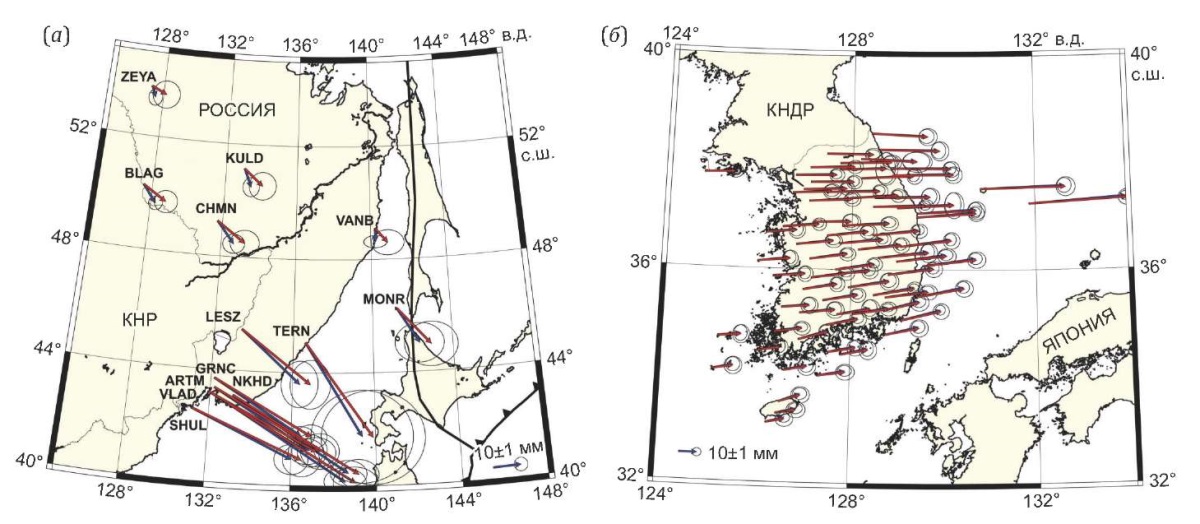
Рис. 3. Сравнение исходных (синие векторы) и трансформированных (красные векторы)
косейсмических смещений на территории юга Дальнего Востока России (а) и Южной Кореи (б).
Эллипсы погрешностей вычислены с 95%-ной доверительной вероятностью.
Fig. 3. Comparison of the initially observed (blue vectors)
and transformed (red vectors) coseismic displacements
determined on the territory of the south of the Russian Far East (a) and South Korea (б).
Error ellipses were calculated with 95 % confidence level.
Из рис. 3 видно, что при объединении данные южно-корейской ГНСС-сети претерпели незначительные изменения и с большей точностью были «вписаны» в поле косейсмических смещений, полученных на территории Китая в работе [Wang et al., 2011], нежели векторы косейсмических подвижек юга российского Дальнего Востока, величины которых после трансформирования возросли от 8 до ~44 % относительно исходных значений, соответственно, для пунктов, расположенных на юге (зарегистрированы наиболее значительные смещения) и в северных и северо-восточных областях исследуемого региона (зарегистрированы малые субсантиметровые подвижки). Полученный эффект в значительной степени объясняется существенно меньшей точностью реализации системы координат в российской сети, опирающейся только на 12 пунктов глобальной сети IGS (в работах [Wang et al., 2011; Baek et al., 2012] система координат задана совокупностью ~100 IGS-станций), что подчеркивает необходимость тщательного выбора исходных пунктов, использующихся для обработки ГНСС-данных, а также важность надежной фиксации системы координат при решении геодинамических задач методами космической геодезии даже в региональных масштабах.
Полученное авторами в дальней относительно очага землетрясения Тохоку зоне единое поле косейсмических движений земной коры Северо-Восточной Азии представлено на рис. 4, а его числовые характеристики приведены в Прил. 1, табл. 1.1. Эти результаты могут использоваться как исходные данные для решения широкого спектра сейсмологических и геодинамических задач, а также для исследования реологического строения литосферы Северо-Восточной Азии. В частности, авторами на их основе с использованием программного пакета GridStrain Ver. 2.0 [Teza et al., 2008] рассчитано единое поле косейсмических деформаций исследуемого региона (рис. 5). Компоненты тензора деформаций вычислялись в узлах сетки с шагом 50 км методом наименьших квадратов. Использованная методика интерполяции данных описана в работе [Shen et al., 1996]. Деформации в точках, значительно удаленных от пунктов ГНСС-наблюдений и имеющие низкий вес, не анализировались.
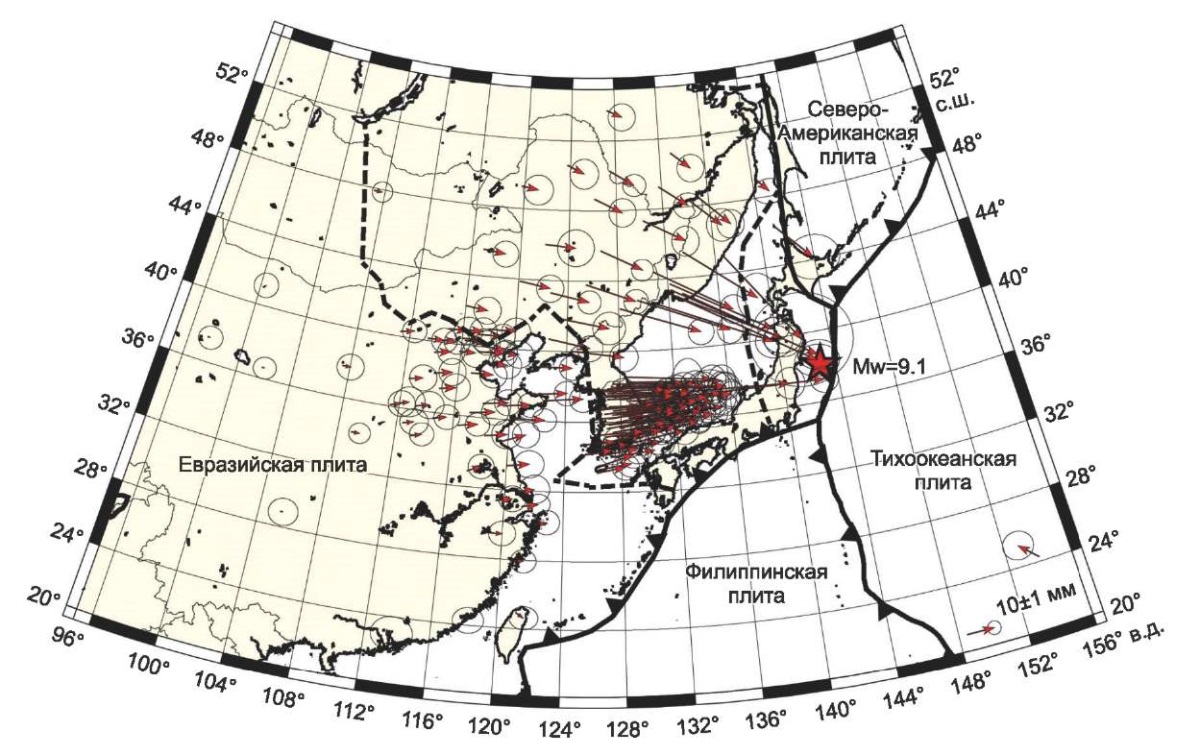
Рис. 4. Объединенное поле косейсмических смещений
в дальней относительно очага землетрясения Тохоку 11.03.2011 г. зоне.
Fig. 4. Combined field of coseismic displacements
in the far-field zone of the 2011 Tohoku earthquake.
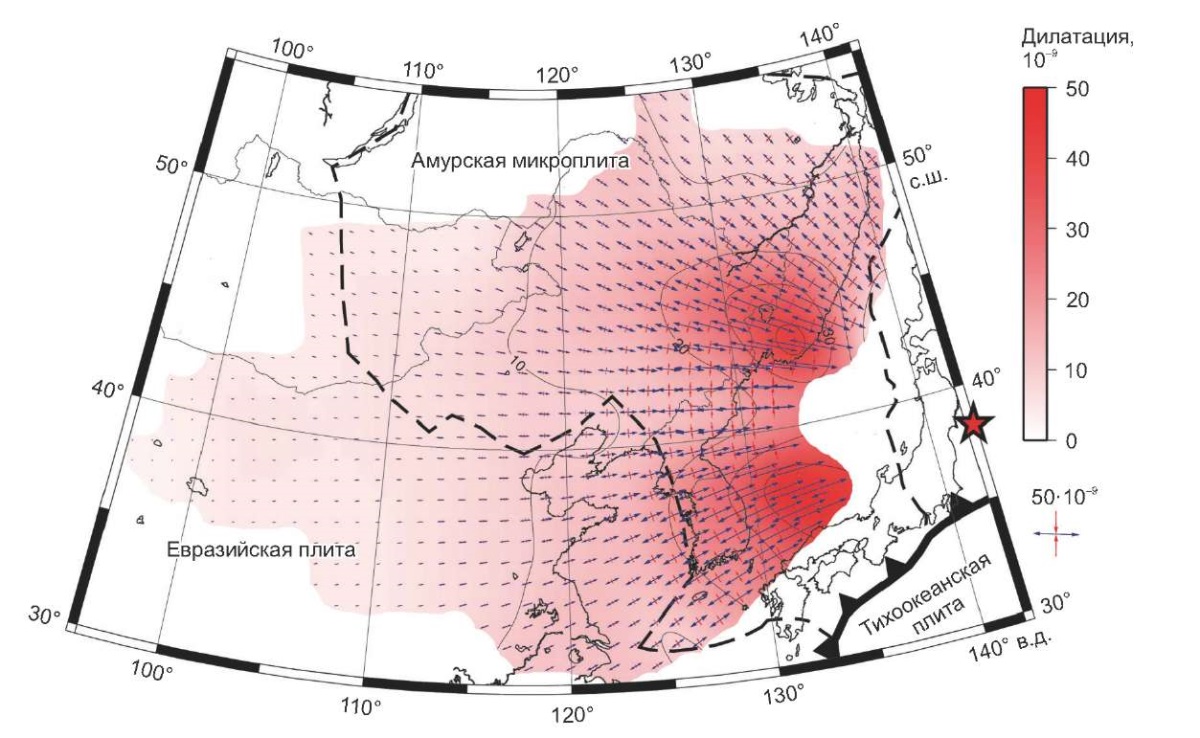
Рис. 5. Объединенное поле косейсмических деформаций
в дальней относительно очага землетрясения Тохоку 2011 г. зоне.
Стрелками показаны оси главных деформаций
(синие − максимальное удлинение (растяжение),
красные − минимальное удлинение (сжатие)). Цветом даны величины дилатации.
Пунктирной линией обозначен один из вариантов положения
границы предполагаемой Амурской микроплиты [Bird, 2003].
Fig. 5. Combined field of coseismic deformations
in the far-field zone of the 2011 Tohoku earthquake.
Axis of principal strains are given by blue (extension) and red (contraction) arrows.
The dilatation rate is given by color gradient.
The dotted line denotes the boundary location
of the hypothesized Amurian microplate according to [Bird, 2003].
Полученные оси и величины главных деформаций приведены на рис. 5. Из него видно, что восточная часть Евразийского континента испытала заметное косейсмическое растяжение, более чем на порядок превышающее фоновые значения среднегодовых скоростей деформаций. Корейский полуостров, южная часть Приморского края и область их сочленения, удаленные на расстояние около 1000 км от очаговой области, демонстрируют наиболее интенсивное растяжение, максимальные значения которого достигают 5·10–8 – 6·10–8, а ориентировка осей максимального удлинения практически совпадает с направлением на эпицентр землетрясения Тохоку 2011 г. Аналогичную картину интенсивного субширотного растяжения этой области демонстрирует поле значений дилатации (рис. 5), величины которой достигают значений 2.5·10–8 – 4.5∙10–8 и более на юге Приморья, на восточном побережье Южной Кореи и к востоку от нее. Величины деформаций достаточно быстро убывают с ростом расстояния от эпицентра и на расстоянии порядка 3000 км от него уменьшаются на порядок и практически совпадают со скоростями фоновых деформаций. Согласно работе [Wang, Shen, 2020], северо-восток Китая в период до землетрясения Тохоку 2011 г. находился в обстановке сжатия, скорости которого равны первым единицам 10–9 год–1. Более детальные оценки компонент тензора деформаций всего рассматриваемого в настоящей работе региона в межсейсмический период анализируются по данным долговременных ГНСС-наблюдений в работе [Ashurkov et al., 2016]. Там также отмечается, что восточная часть Евразийского континента находится в обстановке слабого сжатия (порядка 10–9 год–1) с отдельными «островками» положительных, на 1.0–1.5 порядка больше фоновых, значениями дилатации, как правило, приуроченными к предполагаемым границам блоков и активных геоструктур. Следует отметить, что выделяющаяся по нашим данным в южной части Приморья зона интенсивных косейсмических деформаций растяжения практически совпадает по пространственному положению и величинам с выделенной в работе [Ashurkov et al., 2016] по ГНСС-данным межсейсмического периода положительной дилатационной аномалией (3∙10–8 – 5∙10–8 год–1), что может быть обусловлено особенностями ориентации очага землетрясения Тохоку 2011 г. , либо наличием в этом районе долгоживущих геоструктур, связанных, например, с погружением субдуцирующей Тихоокеанской литосферной плиты и концентрацией глубокофокусной сейсмической активности, наблюдаемой в районе стыка Южного Приморья, Китая и КНДР.
4. ЗАКЛЮЧЕНИЕ
Исследования последних двух десятилетий показали, что сильнейшие землетрясения порождают смещения и деформации земной коры, охватывающие целые регионы мира площадью до нескольких миллионов квадратных километров.
Значения косейсмических смещений, полученные на основе независимой обработки данных разнородных ГНСС-сетей, могут существенно различаться в силу ряда факторов, что способно снизить точность определения параметров моделей различных геофизических процессов, базирующихся на результатах их объединения. Для минимизации таких различий нами предложена, программно реализована и проиллюстрирована на численном примере методика приведения полей косейсмических смещений в дальней относительно очага зоне в единую систему при помощи шестипараметрического преобразования Гельмерта аналогично комбинированию скоростей и координат геодезических сетей. Предлагаемая методика и полученное объединенное поле косейсмических смещений и деформаций северо-восточной окраины Евразийского континента могут использоваться как исходный материал для решения различных геофизических задач в рамках российских и международных проектов, объединяющих данные обширных ГНСС-сетей, и анализа происходящих в регионе геодинамических процессов.
5. БЛАГОДАРНОСТИ
Авторы благодарят рецензентов за конструктивные замечания, позволившие существенно улучшить содержание работы, а также ООО «Меридиан», ООО «Аэрофотопром», ООО «Гео-Плюс» за предоставление данных ГНСС-наблюдений, доктора Giordano Teza – за предоставление программного пакета GridStrain. Для построения рисунков частично использовался программный пакет GMT.
6. ЗАЯВЛЕННЫЙ ВКЛАД АВТОРОВ / CONTRIBUTION OF THE AUTHORS
Н.В. Шестаков − концептуализация, выполнение расчетов, написание работы и ее редактирование. А.К. Кишкина − написание и редактирование работы. Остальные авторы − предоставление данных ГНСС-наблюдений, редактирование и обсуждение работы.
N.V. Shestakov – conceptualization, calculations, the drafting of and editing the work. A.K. Kishkina – writing and editing the work. Other authors – providing GNSS observation data, editing and discussing the work.
7. РАСКРЫТИЕ ИНФОРМАЦИИ / DISCLOSURE
Авторы заявляют об отсутствии конфликта интересов. Авторы прочли и одобрили финальную версию перед публикацией.
The authors declare that they have no conflicts of interest to declare. The authors read and approved the final manuscript.
ПРИЛОЖЕНИЕ 1 / APPENDIX 1
Таблица 1.1. Объединенное поле трансформированных косейсмических смещений
по направлениям «Север – Юг» (dN) и «Восток – Запад» (dE)
Table 1.1. The combined field of the transformed coseismic displacements
in the directions "North – South" (dN) and "East – West" (dE)
Наименование пункта | Положение пункта | Косейсмические смещения | ||
Широта | Долгота | dE, мм | dN, мм | |
BHAO | 128.980° | 36.160° | 27.9±2.1 | 3.4±1.9 |
JEJU | 126.460° | 33.290° | 11.6±2.2 | 2.1±1.9 |
MKPO | 126.380° | 34.820° | 15.5±1.9 | 2.0±1.7 |
MLYN | 128.740° | 35.490° | 24.0±2.1 | 3.1±1.8 |
SKCH | 128.560° | 38.250° | 33.8±2.0 | –0.6±2.3 |
SKMA | 126.920° | 37.490° | 24.0±1.7 | 0.8±1.6 |
KOHG | 127.520° | 34.450° | 15.7±1.9 | 2.7±2.0 |
ANHN | 126.140° | 36.670° | 16.9±1.9 | 1.6±2.0 |
CCHN | 127.720° | 37.990° | 28.4±2.2 | 0.8±1.8 |
DANG | 126.600° | 34.100° | 13.1±2.1 | 2.5±2.3 |
DOKD | 131.870° | 37.240° | 54.6±2.1 | 3.0±1.9 |
EOCH | 125.970° | 36.130° | 18.1±1.8 | 1.9±2.0 |
GASA | 126.040° | 34.460° | 12.8±1.7 | 1.9±2.0 |
GEOM | 127.320° | 34.010° | 15.5±2.1 | 2.2±1.9 |
HGDO | 125.200° | 34.710° | 12.5±1.9 | 1.1±2.2 |
HOMI | 129.570° | 36.080° | 29.3±2.1 | 3.6±2.0 |
JEOJ | 128.400° | 38.550° | 31.0±2.1 | –1.7±2.1 |
JUKB | 129.430° | 37.060° | 32.6±2.0 | 1.8±2.2 |
JUMN | 128.830° | 37.900° | 33.4±1.9 | –0.2±2.0 |
MARA | 126.270° | 33.120° | 10.3±2.0 | 2.0±1.9 |
MLDO | 126.320° | 35.860° | 17.8±1.8 | 1.4±1.9 |
MOOJ | 127.580° | 35.900° | 21.2±1.9 | 2.5±1.9 |
PYCH | 128.490° | 37.350° | 30.7±2.1 | 0.5±2.3 |
SEOI | 128.740° | 34.790° | 19.1±2.1 | 4.0±2.1 |
SOCH | 124.730° | 37.760° | 16.9±1.8 | 0.8±1.6 |
SOHE | 125.100° | 34.090° | 11.6±2.0 | 2.0±2.1 |
SORI | 127.800° | 34.410° | 15.4±2.0 | 2.8±2.3 |
SUWN | 127.054° | 37.276° | 23.8±1.9 | 1.3±1.7 |
ULLE | 130.800° | 37.520° | 47.4±2.2 | 1.2±2.3 |
YNDO | 129.070° | 35.060° | 22.7±1.8 | 5.5±1.9 |
BOEN | 127.730° | 36.490° | 24.3±1.8 | 2.4±1.7 |
CHCN | 127.710° | 37.870° | 25.7±2.5 | 0.8±4.0 |
CHEN | 127.160° | 36.880° | 20.9±2.1 | 0.4±2.0 |
CHJU | 126.530° | 33.510° | 11.9±2.1 | 4.0±2.0 |
CHLW | 127.420° | 38.160 | 25.7±2.0 | –0.2±1.6 |
CHNG | 128.480° | 35.530° | 23.1±1.8 | 4.1±1.6 |
CHSG | 129.060° | 36.440° | 28.3±1.9 | 3.6±2.0 |
CHWN | 128.690° | 35.240° | 20.5±2.1 | 5.0±2.1 |
CHYG | 126.800° | 36.460° | 20.5±2.0 | 2.4±1.7 |
CNJU | 127.460° | 36.630° | 22.8±1.9 | 2.6±1.7 |
DOND | 127.060° | 37.900° | 24.7±1.8 | 0.7±1.6 |
GOCH | 127.940° | 35.670 | 22.9±2.1 | 3.7±2.1 |
GSAN | 127.790° | 36.820° | 26.0±2.0 | 1.6±1.7 |
HADG | 127.710° | 35.160° | 18.7±2.1 | 3.3±2.4 |
HONC | 128.190° | 37.710° | 29.4±1.8 | 1.6±1.9 |
INCH | 126.690° | 37.420° | 21.7±2.0 | 1.2±1.8 |
INJE | 128.170° | 38.070° | 31.2±3.3 | –1.4±2.5 |
JAHG | 126.900° | 34.680° | 16.4±2.1 | 4.8±1.9 |
JINJ | 128.050° | 35.170° | 19.8±1.9 | 3.4±1.7 |
JUNG | 126.970° | 35.620° | 18.9±1.7 | 3.3±1.9 |
JUNJ | 127.140° | 35.840° | 19.4±1.9 | 2.7±1.7 |
KANR | 128.870° | 37.770° | 33.8±2.0 | 0.5±2.0 |
KUNW | 128.570° | 36.230° | 28.3±2.0 | 3.0±2.3 |
KWNJ | 126.910° | 35.180° | 19.8±2.0 | 1.9±2.0 |
MUJU | 127.660° | 36.000° | 21.6±1.8 | 3.3±1.7 |
NAMW | 127.400° | 35.420° | 19.4±1.8 | 3.3±1.8 |
NONS | 127.100° | 36.190° | 20.8±1.9 | 3.1±1.6 |
PAJU | 126.740° | 37.750° | 22.7±1.7 | 0.5±1.6 |
SEOS | 126.490° | 36.780 | 20.1±1.6 | 1.8±1.5 |
SNJU | 128.140° | 36.380° | 24.0±1.9 | 2.7±1.9 |
SONC | 127.490° | 34.960° | 17.6±1.9 | 3.6±1.9 |
SOUL | 127.080° | 37.630° | 23.9±1.7 | 0.3±1.7 |
TABK | 128.980° | 37.160° | 31.6±2.2 | 1.8±3.2 |
TEGN | 128.800° | 35.910° | 25.3±2.0 | 3.5±2.0 |
WNJU | 127.950° | 37.340° | 26.6±1.7 | 1.8±1.6 |
WOLS | 129.420° | 35.500° | 26.3±2.0 | 5.0±2.0 |
WULJ | 129.410° | 36.990° | 33.1±1.8 | 2.2±1.9 |
YANP | 127.510° | 37.450° | 27.6±1.8 | 0.7±1.7 |
YECH | 128.450° | 36.650° | 25.8±1.9 | 2.7±1.8 |
YONK | 126.520° | 35.280° | 15.6±1.9 | 1.2±2.0 |
YOWL | 128.460° | 37.180° | 29.1±1.8 | 0.5±1.7 |
ARTM | 132.196° | 43.360° | 39.3±2.8 | –20.6±2.6 |
CHMN | 133.041° | 51.137° | 6.7±2.0 | –6.0±2.0 |
GRNC | 132.166° | 43.698° | 36.1±2.3 | –19.0±1.7 |
KULD | 131.738° | 49.236° | 10.2±2.1 | –7.4±1.9 |
BLAG | 127.521° | 50.257° | 8.6±1.7 | –5.3±1.6 |
VANB | 140.255° | 49.091° | 4.4±2.4 | –5.1±1.8 |
VLAD | 131.926° | 43.197° | 40.2±2.8 | –19.2±2.2 |
ZEYA | 127.286° | 53.757° | 5.4±2.0 | –2.4±2.0 |
SHUL | 131.157° | 42.581° | 40.8±2.7 | –15.9±2.4 |
LESZ | 133.385° | 45.469° | 25.6±3.0 | –18.8±3.6 |
PART | 133.126° | 43.123° | 46.8±2.9 | –26.0±2.2 |
NKHD | 132.891° | 42.828° | 47.5±3.3 | –26.1±2.3 |
MONR | 141.259° | 46.246° | 11.9±3.9 | –13.1±3.3 |
TERN | 136.601° | 45.062° | 24.9±7.6 | –33.6±6.9 |
AHBB | 117.296° | 32.905° | 5.0±1.9 | 2.0±1.8 |
BJGB | 117.158° | 40.692° | 9.0±1.8 | 0.0±1.8 |
BJSH | 116.224° | 40.251° | 8.0±1.9 | 0.0±1.8 |
BJYQ | 115.968° | 40.370° | 8.0±1.8 | 0.0±1.7 |
DLHA | 97.378° | 37.381° | 1.0±1.8 | 0.0±1.7 |
DXIN | 100.201° | 40.984° | 1.0±1.8 | 1.0±1.8 |
GUAN | 113.340° | 23.185° | 2.0±3.1 | –1.0±2.5 |
HAHB | 114.519° | 35.658° | 5.0±1.9 | 1.0±1.8 |
HAJY | 112.447° | 35.163° | 4.0±2.1 | 1.0±1.9 |
HECC | 115.840° | 40.884° | 8.0±2.0 | 0.0±2.0 |
HECD | 117.918° | 41.016° | 10.0±2.1 | 0.0±2.0 |
HECX | 116.931° | 38.465° | 8.0±2.0 | 0.0±1.9 |
HELQ | 114.309° | 38.247° | 6.0±2.0 | 1.0±2.0 |
HELY | 114.707° | 37.399° | 6.0±2.1 | 1.0±2.0 |
HETS | 118.295° | 39.736° | 10.0±2.1 | 0.0±2.0 |
HEYY | 114.156° | 40.127° | 7.0±1.9 | 0.0±1.8 |
HEZJ | 114.900° | 40.828° | 7.0±2.1 | 0.0±2.0 |
HLAR | 119.741° | 49.270° | 6.0±2.2 | –1.0±2.2 |
HLFY | 134.277° | 48.367° | 11.0±2.2 | –10.0±2.4 |
HLHG | 130.236° | 47.353° | 15.0±2.0 | –8.0±2.2 |
HLWD | 126.136° | 48.671° | 10.0±2.0 | –5.0±2.1 |
HRBN | 126.620° | 45.703° | 15.0±1.6 | –7.0±1.6 |
JIXN | 117.530° | 40.076° | 9.0±1.6 | –1.0±1.5 |
JLCB | 128.106° | 42.411° | 29.0±1.9 | –9.0±1.9 |
JLYJ | 129.505° | 42.875° | 33.0±1.9 | –12.0±2.0 |
JSLS | 119.419° | 31.349° | 6.0±2.0 | 1.0±1.9 |
JSLY | 119.467° | 34.722° | 9.0±2.0 | 3.0±1.9 |
JSNT | 120.890° | 31.953° | 6.0±2.2 | 1.0±2.1 |
JSYC | 120.019° | 33.376° | 8.0±2.2 | 1.0±2.0 |
LNDD | 124.327° | 40.032° | 19.0±2.1 | –2.0±2.1 |
LNJZ | 121.740° | 39.092° | 13.0±1.9 | 0.0±1.8 |
LNSY | 123.579° | 41.827° | 17.0±2.4 | –3.0±2.4 |
LNYK | 122.603° | 40.684° | 15.0±1.9 | –3.0±1.9 |
LUZH | 105.414° | 28.872° | 1.0±2.2 | 0.0±2.0 |
NMAG | 122.627° | 43.303° | 14.0±1.7 | –3.0±1.7 |
NMAL | 120.113° | 43.863° | 11.0±2.0 | –2.0±2.0 |
NMDW | 116.963° | 45.513° | 8.0±1.9 | –1.0±1.9 |
NMER | 123.727° | 50.576° | 6.0±2.1 | –3.0±2.2 |
NMTK | 111.252° | 40.261° | 5.0±1.8 | 1.0±1.7 |
NMWL | 122.027° | 46.041° | 11.0±2.7 | –1.0±2.7 |
NMZL | 115.980° | 42.233° | 8.0±2.0 | –1.0±2.0 |
SDCY | 119.460° | 36.754° | 10.0±1.9 | 1.0±1.8 |
SDJX | 116.351° | 35.427° | 7.0±1.8 | 1.0±1.7 |
SDLY | 118.288° | 35.000° | 8.0±2.2 | 1.0±2.1 |
SDQD | 120.304° | 36.077° | 11.0±1.8 | 0.0±1.7 |
SDRC | 122.421° | 37.170° | 14.0±2.0 | 1.0±1.9 |
SDYT | 121.436° | 37.483° | 13.0±1.9 | 1.0±1.8 |
SDZB | 117.992° | 36.806° | 9.0±2.0 | 1.0±1.9 |
SUIY | 130.908° | 44.433° | 28.0±2.0 | –15.0±2.1 |
SXCZ | 113.180° | 36.225° | 5.0±2.1 | 1.0±2.0 |
SXDT | 113.392° | 40.122° | 6.0±1.9 | 0.0±1.8 |
SXGX | 111.900° | 36.252° | 4.0±2.3 | 1.0±2.2 |
SXLF | 111.371° | 36.084° | 4.0±2.0 | 1.0±1.9 |
SXLQ | 114.021° | 39.382° | 6.0±2.0 | 1.0±1.9 |
SXTY | 112.433° | 37.712° | 5.0±2.0 | 1.0±1.9 |
TAIN | 117.123° | 36.214° | 9.0±2.0 | 1.0±1.9 |
TJBD | 117.399° | 39.697° | 9.0±1.9 | 0.0±1.9 |
TJBH | 117.689° | 39.084° | 9.0±2.1 | 0.0±2.0 |
XIAA | 108.986° | 34.178° | 3.0±1.6 | 0.0±1.5 |
XIAM | 118.083° | 24.450° | 1.0±2.3 | –1.0±1.9 |
XNIN | 101.774° | 36.601 | 1.0±1.7 | 0.0±1.6 |
YANC | 107.437° | 37.779° | 3.0±2.0 | 0.0±1.9 |
ZHNZ | 113.105° | 34.521° | 4.0±1.8 | 1.0±1.7 |
ZJJD | 119.274° | 29.475° | 4.0±2.0 | 0.0±1.8 |
ZJWZ | 120.763° | 27.934° | 4.0±1.9 | 0.0±1.7 |
ZJZS | 121.989° | 30.071° | 5.0±1.9 | 1.0±1.8 |
TWTF | 121.165° | 24.954° | 3.0±2.1 | –2.0±1.7 |
ULAB | 107.052° | 47.865° | 3.0±1.5 | 0.0±1.5 |
CHAN | 125.444° | 43.791° | 18.0±1.8 | –6.0±1.8 |
SHAO | 121.200° | 31.100° | 6.0±1.7 | 1.0±1.5 |
DAEJ | 127.374° | 36.399° | 23.0±1.9 | 2.0±1.8 |
MCIL | 153.979° | 24.290° | –6.0±2.3 | 6.0±2.1 |
BJFS | 115.892° | 39.609° | 6.0±2.1 | 0.0±2.1 |
KHAJ | 135.046° | 48.521° | 11.0±2.0 | –11.0±2.1 |
SUWN | 127.054° | 37.276° | 24.0±2.0 | 1.0±1.9 |
Список литературы
1. Altamimi Z., Sillard P., Boucher C., 2002. ITRF2000: A New Release of the International Terrestrial Reference Frame for Earth Science Applications. Journal of Geophysical Research: Solid Earth 121 (В10), ETG 2-1–ETG 2-19. https://doi.org/10.1029/2001JB000561.
2. Ashurkov S.V., Sankov V.A., Serov M.A., Luk’yanov P.Y., Grib N.N., Bordonskii G.S., Dembelov M.G., 2016. Evaluation of Present-Day Deformations in the Amurian Plate and Its Surroundings, Based on GPS Data. Russian Geology and Geophysics 57 (11), 1626–1634. https://doi.org/10.1016/j.rgg.2016.10.008.
3. Baek J., Shin Y.-H., Na S.-H., Shestakov N.V., Park P.-H., Cho S., 2012. Coseismic and Postseismic Crustal Deformations of the Korean Peninsula Caused by the 2011 Mw 9.0 Tohoku Earthquake, Japan, from Global Positioning System Data. Terra Nova 24 (4), 295–300. https://doi.org/10.1111/j.1365-3121.2012.01062.x.
4. Banerjee P., Pollitz F., Burgmann R., 2005. The Size and Duration of the Sumatra-Andaman Earthquake from Far-Field Static Offsets. Science 308 (5729), 1769–1772. https://doi.org/10.1126/science.1113746.
5. Bird P., 2003. An Updated Digital Model of Plate Boundaries. Geochemistry Geophysics Geosystems 4 (3), 1027. https://doi.org/10.1029/2001GC000252.
6. Blewitt G., Hammond W.C., Kreemer C., Plag H-P., Stein S., Okal E., 2009. GPS for Real-Time Earthquake Source Determination and Tsunami Warning Systems. Journal of Geodesy 83, 335–343. https://doi.org/10.1007/s00190-008-0262-5.
7. Быков В.Г., Шестаков Н.В., Герасименко М.Д., Сорокин А.А., Коновалов А.В., Прытков А.С., Василенко Н.Ф., Сафонов Д.А. и др. Единая сеть геодинамических наблюдений ДВО РАН: становление, десять лет развития, основные достижения // Вестник ДВО РАН. 2020. № 3. С. 5–24
8. https://doi.org/10.37102/08697698.2020.211.3.001.
9. Fratarcangeli F., Savastano G., D’Achille M.C., Mazzoni A., Crespi M., Riguzzi F., Devoti R., Pietrantonio G., 2018. VADASE Reliability and Accuracy of Real-Time Displacement Estimation: Application to the Central Italy 2016 Earthquakes. Remote Sensing 10 (8), 1201. https://doi.org/10.3390/rs10081201.
10. Hashimoto M., Choosakul N., Hashizume M., Takemoto S., Takiguchi H., Fukuda Y., Fujimori K., 2006. Crustal Deformations Associated with the Great Sumatra-Andaman Earthquake Deduced from Continuous GPS Observation. Earth Planets Space 58, 127–139. https://doi.org/10.1186/BF03353369.
11. Heki K., Miyazaki S., Takahashi H., Kasahara M., Kimata F., Miura S., Vasilenko N.F., Ivashchenko A., An K., 1999. The Amurian Plate Motion and Current Plate Kinematics in Eastern Asia. Journal of Geophysical Research: Solid Earth 104 (B12), 29147–29155. https://doi.org/10.1029/1999JB900295.
12. Hofmann-Wellenhof B., Lichtenegger H., Walse E., 2008. GNSS – Global Navigation Satellite Systems. GPS, GLONASS, GALILEO and more. Springer-Verlag, Vienna, 518 p. https://doi.org/10.1007/978-3-211-73017-1.
13. Iinuma T., Ohzono M., Ohta Y., Miura S., 2011. Cosesmic Slip Distribution of the 2011 off the Pacific Coast of Tohoku Earthquake (M 9.0) Estimated Based on GPS Data − Was the Asperity in Miyagi-Oki Ruptured? Earth, Planets and Space 63, 24. https://doi.org/10.5047/eps.2011.06.013.
14. Levin V.E., Bakhtiarov V.F., Titkov N.N., Serovetnikov S.S., Magus’kin M.A., Lander A.V., 2014. Contemporary Crustal Movements (CCMS) in Kamchatka. Izvestiya, Physics of the Solid Earth 50, 732–751. https://doi.org/10.1134/S1069351314060044.
15. Lukhnev A.V., Sankov V.A., Miroshnichenko A.I., Ashurkov S.V., Calais E., 2010. GPS Rotation and Strain Rates in the Baikal–Mongolia Region. Russian Geology and Geophysics 51 (7), 785–793. https://doi.org/10.1016/j.rgg.2010.06.006.
16. Pollitz F.F., Bürgmann R., Banerjee P., 2011. Geodetic Slip Model of 2011 M9.0 Tohoku Earthquake. Geophysical Research Letters, 38 (7), L00G08. https://doi.org/10.1029/2011GL048632.
17. Shen Z.-K., Jackson D.D., Ge B.X., 1996. Crustal Deformation across and beyond the Los Angeles Basin from Geodetic Measurements. Journal of Geophysical Research: Solid Earth 101 (В12), 27957–27980. https://doi.org/10.1029/96JB02544.
18. Shestakov N.V., Ohzono M., Takahashi H., Gerasimenko M.D., Bykov V.G., Gordeev E.I., Chebrov V.N., Titkov N.N. et al., 2014. Modeling of Coseismic Crustal Movements Initiated by the May 24, 2013, Mw=8.3 Okhotsk Deep Focus Earthquake. Doklady Earth Sciences 457, 976–981. https://doi.org/10.1134/S1028334X1408008X.
19. Shestakov N.V., Takahashi H., Ohzono M., Prytkov A.S., Bykov V.G., Gerasimenko M.D., Luneva M.N., Gerasimov G.N. et al., 2012. Analysis of the Far-Field Crustal Displacements Caused by the 2011 Great Tohoku Earthquake Inferred from Continuous GPS Observations. Tectonophysics 524–525, 76–86. https://doi.org/10.1016/j.tecto.2011.12.019.
20. Takamatsu N., Muramatsu H., Abe S., Hatanaka Y., Furuya T., Kakiage Y., Ohashi K., Kato C., Ohno K., Kawamoto S., 2023. New GEONET Analysis Strategy at GSI: Daily Coordinates of over 1300 GNSS CORS in Japan throughout the Last Quarter Century. Earth Planets Space 75, 49. https://doi.org/10.1186/s40623-023-01787-7.
21. Teza G., Pesci A., Galgaro A., 2008. Grid_Strain and Grid_ Strain3: Software Packages for Strain Field Computation in 2D and 3D Environment. Computers & Geosciences 34 (9), 1142–1153. https://doi.org/10.1016/j.cageo.2007.07.006.
22. Tregoning P., Burgette R., McClusky S.C., Lejeune S., Watson C.S., McQueen H., 2013. A Decade of Horizontal Deformation from Great Earthquakes. Journal of Geophysical Research: Solid Earth 118 (5), 2371–2381. https://doi.org/10.1002/jgrb.50154.
23. Wang M., Li Q., Wang F., Zhang R., Wang Y., Shi H., Zhang P., Shen Z., 2011. Far-Field Coseismic Displacements Associated with the 2011 Tohoku-Oki Earthquake in Japan Observed by Global Positioning System. Chinese Science Bulletin 56, 2419−2424, https://doi.org/10.1007/s11434-011-4588-7.
24. Wang M., Shen Z.K., 2020. Present-Day Crustal Deformation of Continental China Derived from GPS and Its Tectonic Implications. Journal of Geophysical Research: Solid Earth 125 (2), e2019JB018774. https://doi.org/10.1029/2019JB018774.
25. Zonenshain L.P., Savostin L.A., 1981. Geodynamics of the Baikal Rift Zone and Plate Tectonics of Asia. Tectonophysics 76 (1–2), 1–45. https://doi.org/10.1016/0040-1951(81)90251-1.
Об авторах
Н. В. ШестаковРоссия
690922, Владивосток, о. Русский, пос. Аякс, 10; 690041, Владивосток, ул. Радио, 7
М. Д. Герасименко
Россия
690041, Владивосток, ул. Радио, 7
А. К. Кишкина
Россия
690922, Владивосток, о. Русский, пос. Аякс, 10
В. Г. Быков
Россия
680000, Хабаровск, ул. Ким Ю. Чена, 65
В. В. Пупатенко
Россия
680000, Хабаровск, ул. Ким Ю. Чена, 65
А. С. Прытков
Россия
693022, Южно-Сахалинск, ул. Науки, 1Б
Н. Ф. Василенко
Россия
693022, Южно-Сахалинск, ул. Науки, 1Б
В. С. Жижерин
Россия
675000, Благовещенск, пер. Релочный, 1
С. В. Яковенко
Россия
690041, Владивосток, ул. Балтийская, 43
Рецензия
Для цитирования:
Шестаков Н.В., Герасименко М.Д., Кишкина А.К., Быков В.Г., Пупатенко В.В., Прытков А.С., Василенко Н.Ф., Жижерин В.С., Яковенко С.В. МЕТОДИКА ОБЪЕДИНЕНИЯ КОСЕЙСМИЧЕСКИХ СМЕЩЕНИЙ ЗЕМНОЙ КОРЫ ПО ДАННЫМ РАЗНОРОДНЫХ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ: НА ПРИМЕРЕ МЕГАЗЕМЛЕТРЯСЕНИЯ ТОХОКУ 11.03.2011 г., Mw 9.1. Геодинамика и тектонофизика. 2024;15(1):0736. https://doi.org/10.5800/GT-2024-15-1-0736. EDN: HQCNAT
For citation:
Shestakov N.V., Gerasimenko М.D., Kishkina А.К., Bykov V.G., Pupatenko V.V., Prytkov А.S., Vasilenko N.F., Zhizherin V.S., Yakovenko S.V. METHODOLOGY OF COSEISMIC DISPLACEMENTS COMBINATION OBTAINED BY DATA STEMMING FROM HETEROGENEOUS GEODETIC NETWORKS: ON THE EXAMPLE OF THE GREAT 2011 TOHOKU EARTHQUAKE, Mw 9.1. Geodynamics & Tectonophysics. 2024;15(1):0736. (In Russ.) https://doi.org/10.5800/GT-2024-15-1-0736. EDN: HQCNAT
JATS XML




















































